| Revision as of 10:49, 29 July 2019 editDVdm (talk | contribs)Autopatrolled, Extended confirmed users, New page reviewers, Pending changes reviewers, Rollbackers138,467 edits Undid revision 908375890 by 141.2.17.21 (talk) this statement is about the single above formulaTag: Undo← Previous edit | Revision as of 11:28, 29 July 2019 edit undoJayBeeEll (talk | contribs)Extended confirmed users, New page reviewers28,146 edits yes but it should still be spelled correctlyTag: UndoNext edit → | ||
| Line 228: | Line 228: | ||
| :<math>\sum_{i=1}^{n-1} \left\lfloor \frac{im}{n} \right\rfloor = \frac{1}{2}(m - 1)(n - 1).</math> | :<math>\sum_{i=1}^{n-1} \left\lfloor \frac{im}{n} \right\rfloor = \frac{1}{2}(m - 1)(n - 1).</math> | ||
| The |
The last formula can be generalized for all '' m '' and '' n '' strictly positive integers:<ref>, Master's thesis, page 17.</ref>{{better source}} | ||
| :<math>\sum_{k = 1}^{n - 1} \left\lfloor \frac{k m}{n} \right\rfloor = \frac{(m - 1)(n - 1)+\gcd(m,n)-1}2.</math> | :<math>\sum_{k = 1}^{n - 1} \left\lfloor \frac{k m}{n} \right\rfloor = \frac{(m - 1)(n - 1)+\gcd(m,n)-1}2.</math> | ||
Revision as of 11:28, 29 July 2019
For other uses, see Floor (disambiguation) and Ceiling (disambiguation).Floor and ceiling functions
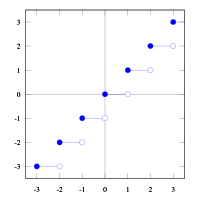 Floor function
Floor function Ceiling function
Ceiling function
In mathematics and computer science, the floor function is the function that takes as input a real number and gives as output the greatest integer less than or equal to , denoted . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted .
For example, and while .
Notation
The notion of the integral part or integer part of x was first introduced by Adrien-Marie Legendre under the name entier (French for "integer") in 1798, when he needed the concept for his proof of the Legendre's formula.
Carl Friedrich Gauss introduced the square bracket notation in his third proof of quadratic reciprocity (1808). This remained the standard in mathematics until Kenneth E. Iverson introduced the names "floor" and "ceiling" and the corresponding notations and in his 1962 book A Programming Language. Both notations are now used in mathematics; this article follows Iverson.
In mathematics, the floor function can also be written with boldface or double brackets . The ceiling function has another notation with reversed boldface or double brackets APL uses ⌊x; other computer languages commonly use notations like entier(x) (ALGOL), INT(x) (BASIC, MS Excel), or floor(x)(C, C++, R, and Python).
The ceiling function is usually denoted by ceil(x) or less commonly ceiling(x) in non-APL computer languages that have a notation for this function. The J Programming Language, a follow on to APL that is designed to use standard keyboard symbols, uses >. for ceiling and <. for floor.
The fractional part is the sawtooth function, denoted by for real x and defined by the formula
For all x,
Examples
| x | Floor | Ceiling | Fractional part |
|---|---|---|---|
| 2 | 2 | 2 | 0 |
| 2.4 | 2 | 3 | 0.4 |
| 2.9 | 2 | 3 | 0.9 |
| −2.7 | −3 | −2 | 0.3 |
| −2 | −2 | −2 | 0 |
Typesetting
The floor and ceiling functions are usually typeset with left and right square brackets where the upper (for floor function) or lower (for ceiling function) horizontal bars are missing. These characters are provided in Unicode:
- U+2308 ⌈ LEFT CEILING (⌈, ⌈)
- U+2309 ⌉ RIGHT CEILING (⌉, ⌉)
- U+230A ⌊ LEFT FLOOR (⌊, ⌊)
- U+230B ⌋ RIGHT FLOOR (⌋, ⌋)
In the LaTeX typesetting system these symbols can be specified with the \lfloor, \rfloor, \lceil and \rceil commands in math mode.
Definition and properties
In the following formulas, x and y are real numbers, k, m, and n are integers, and is the set of integers (positive, negative, and zero).
Floor and ceiling may be defined by the set equations
Since there is exactly one integer in a half-open interval of length one, for any real x there are unique integers m and n satisfying
Then and may also be taken as the definition of floor and ceiling.
Equivalences
These formulas can be used to simplify expressions involving floors and ceilings.
In the language of order theory, the floor function is a residuated mapping, that is, part of a Galois connection: it is the upper adjoint of the function that embeds the integers into the reals.
These formulas show how adding integers to the arguments affect the functions:
The above are never true if n is not an integer; however, for every x, y the following inequalities hold:
Relations among the functions
It is clear from the definitions that
- with equality if and only if x is an integer, i.e.
In fact, for integers n:
Negating the argument switches floor and ceiling and changes the sign:
and:
Negating the argument complements the fractional part:
The floor, ceiling, and fractional part functions are idempotent:
The result of nested floor or ceiling functions is the innermost function:
Quotients
If m and n are integers and n ≠ 0,
If n is a positive integer
If m is positive
For m = 2 these imply
More generally, for positive m (See Hermite's identity)
The following can be used to convert floors to ceilings and vice versa (m positive)
If m and n are positive and coprime, then
The last formula can be generalized for all m and n strictly positive integers:
Since the right-hand side is symmetrical in m and n, this implies that
More generally, if m and n are positive,
This is sometimes called a reciprocity law.
Nested divisions
For positive integer n, and arbitrary real numbers m,x:
Continuity and series expansions
None of the functions discussed in this article are continuous, but all are piecewise linear: the functions , , and have discontinuities at the integers.
is upper semi-continuous and and are lower semi-continuous.
Since none of the functions discussed in this article are continuous, none of them have a power series expansion. Since floor and ceiling are not periodic, they do not have uniformly convergent Fourier series expansions. The fractional part function has Fourier series expansion
for x not an integer.
At points of discontinuity, a Fourier series converges to a value that is the average of its limits on the left and the right, unlike the floor, ceiling and fractional part functions: for y fixed and x a multiple of y the Fourier series given converges to y/2, rather than to x mod y = 0. At points of continuity the series converges to the true value.
Using the formula floor(x) = x − {x} gives
for x not an integer.
Applications
Mod operator
For an integer x and a positive integer y, the modulo operation, denoted by x mod y, gives the value of the remainder when x is divided by y. This definition can be extended to real x and y, y ≠ 0, by the formula
Then it follows from the definition of floor function that this extended operation satisfies many natural properties. Notably, x mod y is always between 0 and y, i.e.,
if y is positive,
and if y is negative,
Quadratic reciprocity
Gauss's third proof of quadratic reciprocity, as modified by Eisenstein, has two basic steps.
Let p and q be distinct positive odd prime numbers, and let
First, Gauss's lemma is used to show that the Legendre symbols are given by
and
The second step is to use a geometric argument to show that
Combining these formulas gives quadratic reciprocity in the form
There are formulas that use floor to express the quadratic character of small numbers mod odd primes p:
Rounding
For an arbitrary real number , rounding to the nearest integer with tie breaking towards positive infinity is given by ; rounding towards negative infinity is given as .
If tie-breaking is away from 0, then the rounding function is , and rounding towards even, as is usual in the nearest integer function, can be expressed with the more cumbersome , which is the above expression for rounding towards positive infinity minus an integrality indicator for .
Truncation
The truncation of a positive number is given by The truncation of a negative number is given by . Obviously the truncation of is itself .
The truncation of any real number can be given by: , where sgn(x) is the sign function.
Number of digits
The number of digits in base b of a positive integer k is
Factors of factorials
Let n be a positive integer and p a positive prime number. The exponent of the highest power of p that divides n! is given by the formula
where is the way of writing n in base p. Note that this is a finite sum, since the floors are zero when p > n.
Beatty sequence
The Beatty sequence shows how every positive irrational number gives rise to a partition of the natural numbers into two sequences via the floor function.
Euler's constant (γ)
There are formulas for Euler's constant γ = 0.57721 56649 ... that involve the floor and ceiling, e.g.
and
Riemann function (ζ)
The fractional part function also shows up in integral representations of the Riemann zeta function. It is straightforward to prove (using integration by parts) that if is any function with a continuous derivative in the closed interval ,
Letting for real part of s greater than 1 and letting a and b be integers, and letting b approach infinity gives
This formula is valid for all s with real part greater than −1, (except s = 1, where there is a pole) and combined with the Fourier expansion for {x} can be used to extend the zeta function to the entire complex plane and to prove its functional equation.
For s = σ + i t in the critical strip (i.e. 0 < σ < 1),
In 1947 van der Pol used this representation to construct an analogue computer for finding roots of the zeta function.
Formulas for prime numbers
The floor function appears in several formulas characterizing prime numbers. For example, since is equal to 1 if m divides n, and to 0 otherwise, it follows that a positive integer n is a prime if and only if
One may also give formulas for producing the prime numbers. For example, let pn be the n prime, and for any integer r > 1, define the real number α by the sum
Then
A similar result is that there is a number θ = 1.3064... (Mills' constant) with the property that
are all prime.
There is also a number ω = 1.9287800... with the property that
are all prime.
Let π(x) be the number of primes less than or equal to x. It is a straightforward deduction from Wilson's theorem that
Also, if n ≥ 2,
None of the formulas in this section are of any practical use.
Solved problems
Ramanujan submitted these problems to the Journal of the Indian Mathematical Society.
If n is a positive integer, prove that
(i)
(ii)
(iii)
Unsolved problem
The study of Waring's problem has led to an unsolved problem:
Are there any positive integers k ≥ 6 such that
- ?
Mahler has proved there can only be a finite number of such k; none are known.
Computer implementations

In most programming languages, the simplest method to convert a floating point number to an integer does not do floor or ceiling, but truncation. This is historical, as the first machines used ones' complement and truncation was simpler to implement (floor is simpler in two's complement). FORTRAN was defined to require this behavior and thus almost all processors implement conversion this way. Some consider this to be an unfortunate historical design decision that has led to bugs handling negative offsets and graphics on the negative side of the origin.
A bit-wise right-shift of a signed integer by is the same as . Division by a power of 2 is often written as a right-shift, not for optimization as might be assumed, but because the floor of negative results is required. Assuming such shifts are "premature optimization" and replacing them with division can break software.
Many programming languages (including C, C++, Java, PHP, R, and Python) provide standard functions for floor and ceiling, usually called floor and ceil.
Spreadsheet software
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (August 2008) (Learn how and when to remove this message) |
Most spreadsheet programs support some form of a ceiling function. Although the details differ between programs, most implementations support a second parameter—a multiple of which the given number is to be rounded to. For example, ceiling(2, 3) rounds 2 up to the nearest multiple of 3, giving 3. The definition of what "round up" means, however, differs from program to program.
Until Excel 2010, Microsoft Excel's ceiling function was incorrect for negative arguments; ceiling(-4.5) was -5. This has followed through to the Office Open XML file format. Excel 2010 now follows the standard definition. Meanwhile, its roundup function continues to round away from zero.
The OpenDocument file format, as used by OpenOffice.org, Libreoffice and others, follows the mathematical definition of ceiling for its ceiling function, with an optional parameter for Excel compatibility. For example, CEILING(-4.5) returns −4.
See also
Notes
- Graham, Knuth, & Patashnik, Ch. 3.1
- Lemmermeyer, pp. 10, 23.
- e.g. Cassels, Hardy & Wright, and Ribenboim use Gauss's notation, Graham, Knuth & Patashnik, and Crandall & Pomerance use Iverson's.
- Iverson, p. 12.
- Higham, p. 25.
- See the Wolfram MathWorld article.
- Mathwords: Floor Function.
- Mathwords: Ceiling Function
- Sullivan, p. 86.
- "Vocabulary". J Language. Retrieved 6 September 2011.
- Graham, Knuth, & Patashnik, p. 70.
- Graham, Knuth, & Patashink, Ch. 3
- Graham, Knuth, & Patashnik, p. 73
- Graham, Knuth, & Patashnik, p. 85
- Graham, Knuth, & Patashnik, p. 85 and Ex. 3.15
- Graham, Knuth, & Patashnik, Ex. 3.12
- J.E.blazek, Combinatoire de N-modules de Catalan, Master's thesis, page 17.
- Graham, Knuth, & Patashnik, p. 94
- Graham, Knuth, & Patashnik, p. 71, apply theorem 3.10 with x/m as input and the division by n as function
- Titchmarsh, p. 15, Eq. 2.1.7
- Lemmermeyer, § 1.4, Ex. 1.32–1.33
- Hardy & Wright, §§ 6.11–6.13
- Lemmermeyer, p. 25
- Hardy & Wright, Th. 416
- Graham, Knuth, & Patashnik, pp. 77–78
- These formulas are from the Misplaced Pages article Euler's constant, which has many more.
- Titchmarsh, p. 13
- Titchmarsh, pp.14–15
- Crandall & Pomerance, p. 391
- Crandall & Pomerance, Ex. 1.3, p. 46. The infinite upper limit of the sum can be replaced with n. An equivalent condition is n > 1 is prime if and only if .
- Hardy & Wright, § 22.3
- ^ Ribenboim, p. 186
- Ribenboim, p. 181
- Crandall & Pomerance, Ex. 1.4, p. 46
- Ribenboim, p.180 says that "Despite the nil practical value of the formulas ... may have some relevance to logicians who wish to understand clearly how various parts of arithmetic may be deduced from different axiomatzations ... "
- Hardy & Wright, pp.344—345 "Any one of these formulas (or any similar one) would attain a different status if the exact value of the number α ... could be expressed independently of the primes. There seems no likelihood of this, but it cannot be ruled out as entirely impossible."
- Ramanujan, Question 723, Papers p. 332
- Hardy & Wright, p. 337
- Mahler, K. On the fractional parts of the powers of a rational number II, 1957, Mathematika, 4, pages 122-124
- "C++ reference of
floorfunction". Retrieved 5 December 2010. - "C++ reference of
ceilfunction". Retrieved 5 December 2010. - "Math (Java SE 9 & JDK 9 )". docs.oracle.com. Retrieved 20 November 2018.
- "Math (Java SE 9 & JDK 9 )". docs.oracle.com. Retrieved 20 November 2018.
- "PHP manual for
ceilfunction". Retrieved 18 July 2013. - "PHP manual for
floorfunction". Retrieved 18 July 2013. - https://stat.ethz.ch/R-manual/R-devel/library/base/html/Round.html
- "Python manual for
mathmodule". Retrieved 18 July 2013. - But the online help provided in 2010 does not reflect this behavior.
- Microsoft Office Support: ROUNDUP
References
- J.W.S. Cassels (1957), An introduction to Diophantine approximation, Cambridge Tracts in Mathematics and Mathematical Physics, vol. 45, Cambridge University Press
- Crandall, Richard; Pomerance, Carl (2001), Prime Numbers: A Computational Perspective, New York: Springer, ISBN 0-387-94777-9
- Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994), Concrete Mathematics, Reading Ma.: Addison-Wesley, ISBN 0-201-55802-5
- Hardy, G. H.; Wright, E. M. (1980), An Introduction to the Theory of Numbers (Fifth edition), Oxford: Oxford University Press, ISBN 978-0-19-853171-5
- Nicholas J. Higham, Handbook of writing for the mathematical sciences, SIAM. ISBN 0-89871-420-6, p. 25
- ISO/IEC. ISO/IEC 9899::1999(E): Programming languages — C (2nd ed), 1999; Section 6.3.1.4, p. 43.
- Iverson, Kenneth E. (1962), A Programming Language, Wiley
- Lemmermeyer, Franz (2000), Reciprocity Laws: from Euler to Eisenstein, Berlin: Springer, ISBN 3-540-66957-4
- Ramanujan, Srinivasa (2000), Collected Papers, Providence RI: AMS / Chelsea, ISBN 978-0-8218-2076-6
- Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, ISBN 0-387-94457-5
- Michael Sullivan. Precalculus, 8th edition, p. 86
- Titchmarsh, Edward Charles; Heath-Brown, David Rodney ("Roger") (1986), The Theory of the Riemann Zeta-function (2nd ed.), Oxford: Oxford U. P., ISBN 0-19-853369-1
External links
- "Floor function", Encyclopedia of Mathematics, EMS Press, 2001
- Štefan Porubský, "Integer rounding functions", Interactive Information Portal for Algorithmic Mathematics, Institute of Computer Science of the Czech Academy of Sciences, Prague, Czech Republic, retrieved 24 October 2008
- Weisstein, Eric W. "Floor Function". MathWorld.
- Weisstein, Eric W. "Ceiling Function". MathWorld.
 and gives as output the greatest
and gives as output the greatest  . Similarly, the ceiling function maps
. Similarly, the ceiling function maps  .
.
 and
and  while
while  .
.
 in his third proof of
in his third proof of  and
and  in his 1962 book A Programming Language. Both notations are now used in mathematics; this article follows Iverson.
in his 1962 book A Programming Language. Both notations are now used in mathematics; this article follows Iverson.
![{\displaystyle \!]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22cdcec60063e280bedc46afc363a500bfb0eddf) . The ceiling function has another notation with reversed boldface or double brackets
. The ceiling function has another notation with reversed boldface or double brackets ![{\displaystyle ]\!]x<i>x</i>[.
</p><p>For negative values of <i>x</i>, the terms integral part or integer part of <i>x</i> are sometimes instead taken to be the value of the <i>ceiling</i> function, i.e., the value of <i>x</i> rounded to an integer towards 0. The language <a href=](https://wikimedia.org/api/rest_v1/media/math/render/svg/6168c644d2fd4659d34c6176c7ce5f99f6737e4f) APL uses
APL uses  for real x and defined by the formula
for real x and defined by the formula


 is the set of
is the set of 


 and
and  may also be taken as the definition of floor and ceiling.
may also be taken as the definition of floor and ceiling.




 with equality if and only if x is an integer, i.e.
with equality if and only if x is an integer, i.e.




































 ; rounding towards negative infinity is given as
; rounding towards negative infinity is given as  .
.
 , and rounding towards even, as is usual in the
, and rounding towards even, as is usual in the  , which is the above expression for rounding towards positive infinity
, which is the above expression for rounding towards positive infinity  minus an
minus an  .
.
 The truncation of a negative number is given by
The truncation of a negative number is given by  is itself
is itself  , where sgn(x) is the
, where sgn(x) is the 

 is the way of writing n in base p. Note that this is a finite sum, since the floors are zero when p > n.
is the way of writing n in base p. Note that this is a finite sum, since the floors are zero when p > n.



 is any function with a continuous derivative in the closed interval ,
is any function with a continuous derivative in the closed interval ,

 for
for 

 is equal to 1 if m divides n, and to 0 otherwise, it follows that a positive integer n is a prime
is equal to 1 if m divides n, and to 0 otherwise, it follows that a positive integer n is a prime 









 ?
? is the same as
is the same as  . Division by a power of 2 is often written as a right-shift, not for optimization as might be assumed, but because the floor of negative results is required. Assuming such shifts are "premature optimization" and replacing them with division can break software.
. Division by a power of 2 is often written as a right-shift, not for optimization as might be assumed, but because the floor of negative results is required. Assuming such shifts are "premature optimization" and replacing them with division can break software.
 .
.