| Revision as of 20:12, 25 February 2014 edit144.82.161.186 (talk) →Mathematical beauty← Previous edit | Revision as of 20:14, 25 February 2014 edit undoJayBeeEll (talk | contribs)Extended confirmed users, New page reviewers28,152 editsm Undid revision 597116462 by 144.82.161.186 (talk)Next edit → | ||
| Line 62: | Line 62: | ||
| This simple argument is the key to understanding other relations involving {{pi}} and ''e''. | This simple argument is the key to understanding other relations involving {{pi}} and ''e''. | ||
| ==Mathematical beauty |
==Mathematical beauty== | ||
| Euler's identity is often cited |
Euler's identity is often cited as an example of deep ].<ref name=Gallagher2014>{{cite news|last=Gallagher|first=James|title=Mathematics: Why the brain sees maths as beauty|url=http://www.bbc.co.uk/news/science-environment-26151062|accessdate=13 February 2014|newspaper=BBC News online|date=13 February 2014}}</ref> Three of the basic ] operations occur exactly once each: ], ], and ]. The identity also links five fundamental ]s:<ref>Paulos, p. 117.</ref> | ||
| * The ], the additive identity. | * The ], the additive identity. | ||
| * The ], the multiplicative identity. | * The ], the multiplicative identity. | ||
Revision as of 20:14, 25 February 2014
For other uses, see List of topics named after Leonhard Euler § Euler's identities.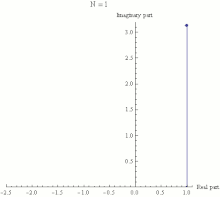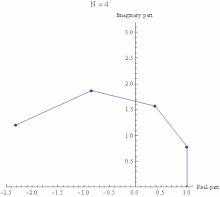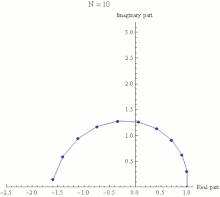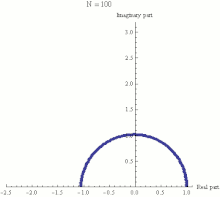
| Part of a series of articles on the |
| mathematical constant e |
|---|
 |
| Properties |
| Applications |
| Defining e |
| People |
| Related topics |
In mathematics, Euler's identity (also known as Euler's equation) is the equality
where
- e is Euler's number, the base of natural logarithms,
- i is the imaginary unit, which satisfies i = −1, and
- π is pi, the ratio of the circumference of a circle to its diameter.
Euler's identity is named after the Swiss mathematician Leonhard Euler. It is considered an example of mathematical beauty.
Explanation

Euler's identity is a special case of Euler's formula from complex analysis, which states that for any real number x,
where the values of the trigonometric functions sine and cosine are given in radians.
In particular, when x = π, or one half-turn (180°) around a circle:
Since
and
it follows that
which yields Euler's identity:
The physical explanation of Euler's identity is that it can be viewed as the group-theoretical definition of the number π. The following discussion is at the physical level, but can be made mathematically strict. The "group" is the group of rotations of a plane around 0. In fact, one can write
with δ being some small angle.
The last equation can be seen as the action of consecutive small shifts along a circle, caused by the application of infinitesimal rotations starting at 1 and continuing through the total length of the arc, connecting points 1 and −1 in the complex plane. Each small shift may then be written as
and the total number of shifts is π/δ. In order to get from 1 to −1, the total transformation would be
Taking the limit when δ → 0, denoting iδ = 1/n and the equation , we arrive at Euler's identity.
π is defined as the total angle which connects 1 to −1 along the arc. Therefore, the relation between π and e arises because a circle can be defined through the action of the group of shifts which preserve the distance between two points on the circle.
This simple argument is the key to understanding other relations involving π and e.
Mathematical beauty
Euler's identity is often cited as an example of deep mathematical beauty. Three of the basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants:
- The number 0, the additive identity.
- The number 1, the multiplicative identity.
- The number π, which is ubiquitous in trigonometry, the geometry of Euclidean space, and analytical mathematics (π = 3.14159265...)
- The number e, the base of natural logarithms, which occurs widely in mathematical, scientific and financial analysis (e = 2.718281828...). Both π and e are transcendental numbers.
- The number i, the imaginary unit of the complex numbers, a field of numbers that contains the roots of all polynomials (that are not constants), and whose study leads to deeper insights into many areas of algebra and calculus.
Furthermore, in algebra and other areas of mathematics, equations are commonly written with zero on one side of the equals sign.
Paul Nahin, a professor emeritus at the University of New Hampshire, states in his book dedicated to Euler's identity and its applications in Fourier analysis that the formula sets "the gold standard for mathematical beauty".
After proving Euler's identity during a lecture, Benjamin Peirce, a noted American 19th-century philosopher, mathematician, and professor at Harvard University, stated that "it is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth." Stanford University mathematics professor Keith Devlin has said, "Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's equation reaches down into the very depths of existence."
The German mathematician Carl Friedrich Gauss was reported to have commented that if this formula was not immediately apparent to a student upon being told it, that student would never be a first-class mathematician.
The mathematics writer Constance Reid claimed that Euler's identity was "the most famous formula in all mathematics". A poll of readers conducted by The Mathematical Intelligencer in 1990 named Euler's identity as the "most beautiful theorem in mathematics". In another poll of readers that was conducted by Physics World in 2004, Euler's identity tied with Maxwell's equations (of electromagnetism) as the "greatest equation ever".
Generalizations
Euler's identity is also a special case of the more general identity that the nth roots of unity, for n > 1, add up to 0:
Euler's identity is the case where n = 2.
In another field of mathematics, by using quaternion exponentiation, one can show that a similar identity also applies to quaternions. Let {i, j, k} be the basis elements, then,
In general, given real a1, a2, and a3 such that , then,
For octonions, with real an such that and the octonion basis elements {i1, i2,..., i7}, then,
History
It has been claimed that Euler's identity appears in his monumental work of mathematical analysis published in 1748, Introductio in analysin infinitorum. However, it is questionable whether this particular concept can be attributed to Euler himself, as he may never have expressed it. (Moreover, while Euler did write in the Introductio about what we today call "Euler's formula", which relates e with cosine and sine terms in the field of complex numbers, the English mathematician Roger Cotes also knew of this formula and Euler may have acquired the knowledge through his Swiss compatriot Johann Bernoulli.)
In popular culture
Euler's identity is referenced in at least two episodes of The Simpsons: Treehouse of Horror VI (1995); and MoneyBart (2010).
See also
Notes and references
Notes
- The term "Euler's identity" (or "Euler identity") is also used elsewhere to refer to other concepts, including the related general formula e = cos x + i sin x, and the Euler product formula.
References
- Dunham, 1999, p. xxiv.
- Stepanov, S.A. (7 February 2011). "Euler identity". Encyclopedia of Mathematics. Retrieved 18 February 2014.
- Gallagher, James (13 February 2014). "Mathematics: Why the brain sees maths as beauty". BBC News online. Retrieved 13 February 2014.
- Paulos, p. 117.
- Cited in Crease, 2007.
- Maor p. 160 and Kasner & Newman pp. 103–104.
- Nahin, 2006, p. 1.
- Derbyshire, p. 210.
- Reid, p. 155.
- Nahin, 2006, pp. 2–3 (poll published in the summer 1990 issue of the magazine).
- Crease, 2004.
- Conway and Guy, pp. 254–255.
- ^ Sandifer, p. 4.
- Euler, p. 147.
- Cohen, David X (2005), "Commentary for "Treehouse of Horror VI", The Simpsons: The Complete Seventh Season, 20th Century Fox.
- Singh, Simon (22 September 2013). "The Simpsons' secret formula: it's written by maths geeks". The Guardian. Retrieved 22 September 2013.
Sources
- Conway, John Horton, and Guy, Richard (1996). The Book of Numbers (Springer, 1996). ISBN 978-0-387-97993-9.
- Crease, Robert P., "The greatest equations ever", PhysicsWeb, October 2004 (registration required).
- Crease, Robert P. "Equations as icons," PhysicsWeb, March 2007 (registration required).
- Dunham, William (1999). Euler: The Master of Us All. Mathematical Association of America. ISBN 978-0-88385-328-3.
- Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (New York: Penguin, 2004).
- Euler, Leonhard. Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus (Leipzig: B. G. Teubneri, 1922).
- Kasner, E., and Newman, J., Mathematics and the Imagination (Simon & Schuster, 1940).
- Maor, Eli, e: The Story of a number (Princeton University Press, 1998). ISBN 0-691-05854-7
- Nahin, Paul J., Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills (Princeton University Press, 2006). ISBN 978-0-691-11822-2
- Paulos, John Allen, Beyond Numeracy: An Uncommon Dictionary of Mathematics (Penguin Books, 1992). ISBN 0-14-014574-5
- Reid, Constance, From Zero to Infinity (Mathematical Association of America, various editions).
- Sandifer, C. Edward. Euler's Greatest Hits (Mathematical Association of America, 2007). ISBN 978-0-88385-563-8










 , we arrive at Euler's identity.
, we arrive at Euler's identity.


 , then,
, then,

 and the octonion basis elements {i1, i2,..., i7}, then,
and the octonion basis elements {i1, i2,..., i7}, then,
