Misplaced Pages

This is an old revision of this page, as edited by 82.142.132.74 (talk) at 07:42, 29 May 2006 (→References and external links). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

This article needs attention from an expert on the subject. Please add a reason or a talk parameter to this template to explain the issue with the article. When placing this tag, consider associating this request with a WikiProject.

General relativity
${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }}$
Introduction History Timeline Tests Mathematical formulation
Fundamental concepts Equivalence principle Special relativity World line Pseudo-Riemannian manifold
Phenomena Kepler problem Gravitational lensing Gravitational redshift Gravitational time dilation Gravitational waves Frame-dragging Geodetic effect Event horizon Singularity Black hole Spacetime Spacetime diagrams Minkowski spacetime Einstein–Rosen bridge
Equations Formalisms Equations Linearized gravity Einstein field equations Friedmann Geodesics Mathisson–Papapetrou–Dixon Hamilton–Jacobi–Einstein Formalisms ADM BSSN Post-Newtonian Advanced theory Kaluza–Klein theory Quantum gravity
Solutions Schwarzschild (interior) Reissner–Nordström Einstein–Rosen waves Wormhole Gödel Kerr Kerr–Newman Kerr–Newman–de Sitter Kasner Lemaître–Tolman Taub–NUT Milne Robertson–Walker Oppenheimer–Snyder pp-wave van Stockum dust Weyl−Lewis−Papapetrou Hartle–Thorne
Scientists Einstein Lorentz Hilbert Poincaré Schwarzschild de Sitter Reissner Nordström Weyl Eddington Friedmann Milne Zwicky Lemaître Oppenheimer Gödel Wheeler Robertson Bardeen Walker Kerr Chandrasekhar Ehlers Penrose Hawking Raychaudhuri Taylor Hulse van Stockum Taub Newman Yau Thorne others
Physics portal  Category
v t e

A gravitational lens is formed when the light from a very distant, bright source (such as a quasar) is "bent" around a massive object (such as a massive galaxy) between the source object and the observer. The process is known as gravitational lensing, and is one of the predictions of Albert Einstein's general relativity theory.

Description

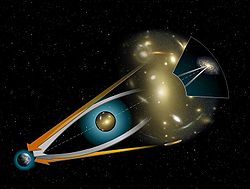
In a gravitational lens, the gravity from the massive object bends light like a lens. As a result, the path of the light from the source is curved, distorting its image, and the apparent location of the source may be different from its actual position. In addition, the observer may see multiple images of a single source. If the source, massive object, and the observer lie on a straight line, the source will appear as a ring behind the massive object. This phenomenon was first mentioned by Chwolson in 1925, and quantified by Einstein in 1936. It is usually referred to in the literature as an Einstein ring, since Chwolson did not concern himself with the flux or radius of the ring image. More commonly, the massive galaxy is off-center, creating a number of images according to the relative positions of the source, lens, and observer, and the shape of the gravitational well of the lensing galaxy.

There are three classes of gravitational lensing:

1. Strong lensing: where there are easily visible distortions such as the formation of Einstein rings, arcs, and multiple images.
2. Weak lensing: where the distortions of background objects are much smaller and can only be detected by analysing large numbers of objects to find distortions of only a few percent.
3. Microlensing: where no distortion in shape can be seen but the amount of light received from a background object changes in time. Typically, both the background source and the lens are stars in the Milky Way.

The effect is weak, such that (in the case of strong lensing) a galaxy having a mass of over 100 billion solar masses will produce multiple images separated by only a few arcseconds. Galaxy clusters can produce separations of several arcminutes. In both cases the galaxies and sources are quite distant, many hundreds of megaparsecs away from our Galaxy.

Gravitational lenses act equally on all kinds of electromagnetic radiation, not just visible light. Weak lensing effects are being studied for the cosmic microwave background as well galaxy surveys. Strong lenses have been observed in radio and x-ray regimes as well. If a strong lens produces multiple images, there will be a relative time delay between two paths: that is, in one image the lensed object will be observed before the other image.

Simulation

To the right is a simulation of gravitational lensing caused by a Schwarzschild black hole going past a background galaxy. A secondary image of the galaxy can be seen within the black hole's Einstein ring on the side opposite the galaxy. The secondary image grows (remaining within the Einstein ring) as the primary image approaches the black hole. The surface brightness of the two images remains constant, but their angular sizes vary, hence producing an amplification of the galaxy luminosity as seen by a distant observer. Maximum amplification occurs when the galaxy (or in this case a bright part of it) is exactly behind the black hole.

History

According to general relativity, gravitational fields "warp" space-time and therefore bend light as a result. This theory was confirmed in 1919 during a solar eclipse, when Arthur Eddington observed the light from stars passing close to the sun was slightly bent, so that stars appeared slightly out of position.

Einstein realized that it was also possible for astronomical objects to bend light, and that under the correct conditions, one would observe multiple images of a single source, called a gravitational lens or sometimes a gravitational mirage. However, as he only considered gravitational lensing by single stars, he concluded that the phenomenon would most likely remain unobserved for foreseeable future. In 1937, Fritz Zwicky first considered the case where a galaxy could act as a lens, something that according to his calculations should be well within the reach of observations.

It was not until 1979 that the first gravitational lens would be discovered. It became known as the "Twin Quasar" since it initially looked like two identical quasars; it is officially named Q0957+561. This gravitational lens was discovered accidentally by Dennis Walsh, Bob Carswell, and Ray Weymann using the Kitt Peak National Observatory 2.1 meter telescope.

The study of gravitational lenses is an important part of the future of astronomy and astrophysics.

Cosmological applications

The most important application of gravitational lensing in cosmology is the weak lensing of galaxies. By measuring the shapes and orientations of large numbers of distant galaxies, their orientations can be averaged to measure the shear of the lensing field in any region. This, in turn, can be used to reconstruct the mass distribution in the area: in particular, the background distribution of dark matter can be reconstructed. Since galaxies are intrinsically elliptical and the weak gravitational lensing signal is small, a very large number of galaxies must be used in these surveys. These weak lensing surveys must carefully avoid a number of important sources of systematic error: the intrinsic shape of galaxies, the tendency of a camera's point spread function to distort the shape of a galaxy and the tendency of atmospheric seeing to distort images must be understood and carefully accounted for. The results of these surveys are important for cosmological parameter estimation, to better understand and improve upon the Lambda-CDM model, and to provide a consistency check on other cosmological observations. They may also provide an important future constraint on dark energy.

Strong gravitational lenses may be used to examine objects at distances at which they would not normally be visible, providing information from further back in time than otherwise possible. Also, not just the object being lensed but the lens itself can provide useful information. By inverting the lens equations information can be gathered on the mass and distribution of the lensing body.

The statistics of strong gravitational lenses can also be used to measure values of cosmological parameters such as the cosmological constant and the mean density of matter in the universe. Presently, the statistics do not place very strong limits on cosmological parameters, partly because the number of strong lenses found is relatively small (less than a hundred).

Another parameter that may come out of the study of gravitational lenses is Hubble's constant which encodes the age and size of the universe. It can be determined, in theory, by measuring two quantities: the angular separation between two images, and the time delay between these images.
There are two contributions to the time delay:

1. the first is the obvious delay due to the difference in optical path length between the two rays.
2. the second is a general relativistic effect, the Shapiro effect, that describes light rays as taking longer to traverse a region of stronger gravitation, (see: gravity well, gravitational time dilation).
   Because the two rays travel through different parts of the potential well created by the deflector, the clocks carrying the source's signal will differ by a small amount.

Astronomical applications

Gravitational lenses can be used as gravitational telescopes, because they magnify objects seen behind them. Researchers at Caltech have used the gravitational lensing afforded by the Abell 2218 cluster of galaxies to detect the most distant galaxy known (February 15, 2004) through imaging with the Hubble Space Telescope.

Gravitational microlensing can provide information on comparatively small astronomical objects, such as MACHOs within our own galaxy, or extrasolar planets (planets beyond the solar system). Three extrasolar planets have been found in this way, and this technique has the promise of finding Earth-mass planets around sunlike stars within the 21st century.

Gravitational lensing can be used to calculate an estimate of the amount of dark matter contained in the lensing body.

Historical papers and references

• Albert Einstein, "Lens-like Action of a Star by the Deviation of Light in the Gravitational Field", Science 84 506 (1936))
• Jurgen Renn, Tilman Sauer and John Stachel, " The Origin of Gravitational Lensing: A Postscript to Einstein's 1936 Science paper", Science 275: 184-186 (1997)

The 1997 review paper lists Chwolson's earlier piece as:

• O.Chwolson, Astron. Nachr 221, 329 (1924)

References and external links

• "XFGLenses". A Computer Program to visualize Gravitational Lenses, Francisco Frutos-Alfaro
• "G-LenS". A Point Mass Gravitational Lens Simulation, Mark Boughen.
• Newbury, Pete, "Gravitational Lensing". Institute of Applied Mathematics, The University of British Columbia.
• Cohen, N., "Gravity's Lens: Views of the New Cosmology", Wiley and Sons, 1988.
• "Q0957+561 Gravitational Lens". Harvard.edu.
• "Gravitational lensing". Gsfc.nasa.gov.
• Bridges, Andrew, "Most distant known object in universe discovered". Associated Press. February 15, 2004. (Farthest galaxy found by gravitational lensing, using Abell 2218 and Hubble Space Telescope.)

• "HST images of strong gravitational lenses". Harvard-Smithsonian Center for Astrophysics.

• "A planetary microlensing event" and "A Jovian-mass Planet in Microlensing Event OGLE-2005-BLG-071" , the first extra-solar planet detections using microlensing.
• Gravitational lensing on arxiv.org

• Astrophysics
• Effects of gravitation