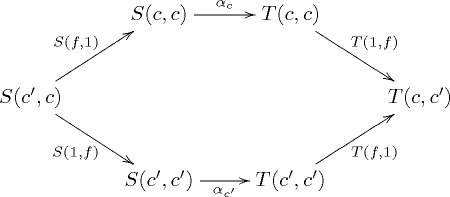
Generalization of natural transformationsIn category theory , a branch of mathematics , a dinatural transformation
α
{\displaystyle \alpha }
functors
S
,
T
:
C
o
p
×
C
→
D
,
{\displaystyle S,T:C^{\mathrm {op} }\times C\to D,}
written
α
:
S
→
¨
T
,
{\displaystyle \alpha :S{\ddot {\to }}T,}
is a function that to every object
c
{\displaystyle c}
C
{\displaystyle C}
α
c
:
S
(
c
,
c
)
→
T
(
c
,
c
)
{\displaystyle \alpha _{c}:S(c,c)\to T(c,c)}
D
{\displaystyle D}
and satisfies the following coherence property : for every morphism
f
:
c
→
c
′
{\displaystyle f:c\to c'}
C
{\displaystyle C}
commutes.
The composition of two dinatural transformations need not be dinatural.
See also
References
Mac Lane, Saunders (2013). Categories for the working mathematician . Springer Science & Business Media. p. 218.
External links
Categories :
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.
**DISCLAIMER** We are not affiliated with Wikipedia, and Cloudflare.
The information presented on this site is for general informational purposes only and does not constitute medical advice.
You should always have a personal consultation with a healthcare professional before making changes to your diet, medication, or exercise routine.
AI helps with the correspondence in our chat.
We participate in an affiliate program. If you buy something through a link, we may earn a commission 💕
↑
between two 
of 
associates an arrow
of 
of 
