Misplaced Pages

Wormhole

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Einstein–Rosen bridges) Hypothetical topological feature of spacetime For other uses, see Wormhole (disambiguation).
A wormhole visualized as a two-dimensional surface. Route (a) is the shortest path through normal space between points 1 and 2; route (b) is a shorter path through a wormhole.
General relativity
Spacetime curvature schematic G μ ν + Λ g μ ν = κ T μ ν {\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }}
Fundamental concepts
Phenomena
Spacetime
  • Equations
  • Formalisms
Equations
Formalisms
Advanced theory
Solutions
Scientists

A wormhole is a hypothetical structure which connects disparate points in spacetime. It may be visualized as a tunnel with two ends at separate points in spacetime (i.e., different locations, different points in time, or both). Wormholes are based on a special solution of the Einstein field equations. Specifically, they are a transcendental bijection of the spacetime continuum, an asymptotic projection of the Calabi–Yau manifold manifesting itself in anti-de Sitter space.

Wormholes are consistent with the general theory of relativity, but whether they actually exist is unknown. Many scientists postulate that wormholes are merely projections of a fourth spatial dimension, analogous to how a two-dimensional (2D) being could experience only part of a three-dimensional (3D) object. A well-known analogy of such constructs is provided by the Klein bottle, displaying a hole when rendered in three dimensions but not in four or higher dimensions.

In 1995, Matt Visser suggested there may be many wormholes in the universe if cosmic strings with negative mass were generated in the early universe. Some physicists, such as Kip Thorne, have suggested how to make wormholes artificially.

Visualization technique

For a simplified notion of a wormhole, space can be visualized as a two-dimensional surface. In this case, a wormhole would appear as a hole in that surface, lead into a 3D tube (the inside surface of a cylinder), then re-emerge at another location on the 2D surface with a hole similar to the entrance. An actual wormhole would be analogous to this, but with the spatial dimensions raised by one. For example, instead of circular holes on a 2-Dimensional plane, the entry and exit points could be visualized as spherical holes in 3D space leading into a four-dimensional "tube" similar to a spherinder.

Another way to imagine wormholes is to take a sheet of paper and draw two somewhat distant points on one side of the paper. The sheet of paper represents a plane in the spacetime continuum, and the two points represent a distance to be traveled, but theoretically, a wormhole could connect these two points by folding that plane (⁠i.e. the paper) so the points are touching. In this way, it would be much easier to traverse the distance since the two points are now touching.

Terminology

In 1928, German mathematician, philosopher and theoretical physicist Hermann Weyl proposed a wormhole hypothesis of matter in connection with mass analysis of electromagnetic field energy; however, he did not use the term "wormhole" (he spoke of "one-dimensional tubes" instead).

American theoretical physicist John Archibald Wheeler (inspired by Weyl's work) coined the term "wormhole". In a 1957 paper that he wrote with Charles W. Misner, they write:

This analysis forces one to consider situations ... where there is a net flux of lines of force, through what topologists would call "a handle" of the multiply-connected space, and what physicists might perhaps be excused for more vividly terming a "wormhole".

— Charles Misner and John Wheeler in Annals of Physics

Modern definitions

Wormholes have been defined both geometrically and topologically. From a topological point of view, an intra-universe wormhole (a wormhole between two points in the same universe) is a compact region of spacetime whose boundary is topologically trivial, but whose interior is not simply connected. Formalizing this idea leads to definitions such as the following, taken from Matt Visser's Lorentzian Wormholes (1996).

If a Minkowski spacetime contains a compact region Ω, and if the topology of Ω is of the form Ω ~ S × Σ, where Σ is a three-manifold of the nontrivial topology, whose boundary has the topology of the form ∂Σ ~ S, and if, furthermore, the hypersurfaces Σ are all spacelike, then the region Ω contains a quasi-permanent intrauniverse wormhole.

Geometrically, wormholes can be described as regions of spacetime that constrain the incremental deformation of closed surfaces. For example, in Enrico Rodrigo's The Physics of Stargates, a wormhole is defined informally as:

a region of spacetime containing a "world tube" (the time evolution of a closed surface) that cannot be continuously deformed (shrunk) to a world line (the time evolution of a point or observer).

Development

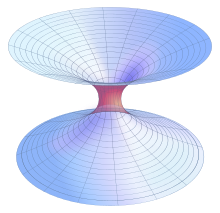
"Embedding diagram" of a Schwarzschild wormhole

Schwarzschild wormholes

The first type of wormhole solution discovered was the Schwarzschild wormhole, which would be present in the Schwarzschild metric describing an eternal black hole, but it was found that it would collapse too quickly for anything to cross from one end to the other. Wormholes that could be crossed in both directions, known as traversable wormholes, were thought to be possible only if exotic matter with negative energy density could be used to stabilize them. However, physicists later reported that microscopic traversable wormholes may be possible and not require any exotic matter, instead requiring only electrically charged fermionic matter with small enough mass that it cannot collapse into a charged black hole. While such wormholes, if possible, may be limited to transfers of information, humanly traversable wormholes may exist if reality can broadly be described by the Randall–Sundrum model 2, a brane-based theory consistent with string theory.

Einstein–Rosen bridges

Einstein–Rosen bridges, also known as ER bridges (named after Albert Einstein and Nathan Rosen), are connections between areas of space that can be modeled as vacuum solutions to the Einstein field equations, and that are now understood to be intrinsic parts of the maximally extended version of the Schwarzschild metric describing an eternal black hole with no charge and no rotation. Here, "maximally extended" refers to the idea that the spacetime should not have any "edges": it should be possible to continue this path arbitrarily far into the particle's future or past for any possible trajectory of a free-falling particle (following a geodesic in the spacetime).

In order to satisfy this requirement, it turns out that in addition to the black hole interior region that particles enter when they fall through the event horizon from the outside, there must be a separate white hole interior region that allows us to extrapolate the trajectories of particles that an outside observer sees rising up away from the event horizon. And just as there are two separate interior regions of the maximally extended spacetime, there are also two separate exterior regions, sometimes called two different "universes", with the second universe allowing us to extrapolate some possible particle trajectories in the two interior regions. This means that the interior black hole region can contain a mix of particles that fell in from either universe (and thus an observer who fell in from one universe might be able to see the light that fell in from the other one), and likewise particles from the interior white hole region can escape into either universe. All four regions can be seen in a spacetime diagram that uses Kruskal–Szekeres coordinates.

In this spacetime, it is possible to come up with coordinate systems such that if a hypersurface of constant time (a set of points that all have the same time coordinate, such that every point on the surface has a space-like separation, giving what is called a 'space-like surface') is picked and an "embedding diagram" drawn depicting the curvature of space at that time, the embedding diagram will look like a tube connecting the two exterior regions, known as an "Einstein–Rosen bridge". The Schwarzschild metric describes an idealized black hole that exists eternally from the perspective of external observers; a more realistic black hole that forms at some particular time from a collapsing star would require a different metric. When the infalling stellar matter is added to a diagram of a black hole's geography, it removes the part of the diagram corresponding to the white hole interior region, along with the part of the diagram corresponding to the other universe.

The Einstein–Rosen bridge was discovered by Ludwig Flamm in 1916, a few months after Schwarzschild published his solution, and was rediscovered by Albert Einstein and his colleague Nathan Rosen, who published their result in 1935. However, in 1962, John Archibald Wheeler and Robert W. Fuller published a paper showing that this type of wormhole is unstable if it connects two parts of the same universe, and that it will pinch off too quickly for light (or any particle moving slower than light) that falls in from one exterior region to make it to the other exterior region.

According to general relativity, the gravitational collapse of a sufficiently compact mass forms a singular Schwarzschild black hole. In the Einstein–Cartan–Sciama–Kibble theory of gravity, however, it forms a regular Einstein–Rosen bridge. This theory extends general relativity by removing a constraint of the symmetry of the affine connection and regarding its antisymmetric part, the torsion tensor, as a dynamic variable. Torsion naturally accounts for the quantum-mechanical, intrinsic angular momentum (spin) of matter. The minimal coupling between torsion and Dirac spinors generates a repulsive spin–spin interaction that is significant in fermionic matter at extremely high densities. Such an interaction prevents the formation of a gravitational singularity (e.g. a black hole). Instead, the collapsing matter reaches an enormous but finite density and rebounds, forming the other side of the bridge.

Although Schwarzschild wormholes are not traversable in both directions, their existence inspired Kip Thorne to imagine traversable wormholes created by holding the "throat" of a Schwarzschild wormhole open with exotic matter (material that has negative mass/energy).

Other non-traversable wormholes include Lorentzian wormholes (first proposed by John Archibald Wheeler in 1957), wormholes creating a spacetime foam in a general relativistic spacetime manifold depicted by a Lorentzian manifold, and Euclidean wormholes (named after Euclidean manifold, a structure of Riemannian manifold).

Traversable wormholes

The Casimir effect shows that quantum field theory allows the energy density in certain regions of space to be negative relative to the ordinary matter vacuum energy, and it has been shown theoretically that quantum field theory allows states where energy can be arbitrarily negative at a given point. Many physicists, such as Stephen Hawking, Kip Thorne, and others, argued that such effects might make it possible to stabilize a traversable wormhole. The only known natural process that is theoretically predicted to form a wormhole in the context of general relativity and quantum mechanics was put forth by Juan Maldacena and Leonard Susskind in their ER = EPR conjecture. The quantum foam hypothesis is sometimes used to suggest that tiny wormholes might appear and disappear spontaneously at the Planck scale, and stable versions of such wormholes have been suggested as dark matter candidates. It has also been proposed that, if a tiny wormhole held open by a negative mass cosmic string had appeared around the time of the Big Bang, it could have been inflated to macroscopic size by cosmic inflation.

Image of a simulated traversable wormhole that connects the square in front of the physical institutes of University of Tübingen with the sand dunes near Boulogne-sur-Mer in the north of France. The image is calculated with 4D raytracing in a Morris–Thorne wormhole metric, but the gravitational effects on the wavelength of light have not been simulated.

Lorentzian traversable wormholes would allow travel in both directions from one part of the universe to another part of that same universe very quickly or would allow travel from one universe to another. The possibility of traversable wormholes in general relativity was first demonstrated in a 1973 paper by Homer Ellis and independently in a 1973 paper by K. A. Bronnikov. Ellis analyzed the topology and the geodesics of the Ellis drainhole, showing it to be geodesically complete, horizonless, singularity-free, and fully traversable in both directions. The drainhole is a solution manifold of Einstein's field equations for a vacuum spacetime, modified by inclusion of a scalar field minimally coupled to the Ricci tensor with antiorthodox polarity (negative instead of positive). (Ellis specifically rejected referring to the scalar field as 'exotic' because of the antiorthodox coupling, finding arguments for doing so unpersuasive.) The solution depends on two parameters: m, which fixes the strength of its gravitational field, and n, which determines the curvature of its spatial cross sections. When m is set equal to 0, the drainhole's gravitational field vanishes. What is left is the Ellis wormhole, a nongravitating, purely geometric, traversable wormhole.

Kip Thorne and his graduate student Mike Morris independently discovered in 1988 the Ellis wormhole and argued for its use as a tool for teaching general relativity. For this reason, the type of traversable wormhole they proposed, held open by a spherical shell of exotic matter, is also known as a Morris–Thorne wormhole.

Later, other types of traversable wormholes were discovered as allowable solutions to the equations of general relativity, including a variety analyzed in a 1989 paper by Matt Visser, in which a path through the wormhole can be made where the traversing path does not pass through a region of exotic matter. However, in the pure Gauss–Bonnet gravity (a modification to general relativity involving extra spatial dimensions which is sometimes studied in the context of brane cosmology) exotic matter is not needed in order for wormholes to exist—they can exist even with no matter. A type held open by negative mass cosmic strings was put forth by Visser in collaboration with Cramer et al., in which it was proposed that such wormholes could have been naturally created in the early universe.

Wormholes connect two points in spacetime, which means that they would in principle allow travel in time, as well as in space. In 1988, Morris, Thorne and Yurtsever worked out how to convert a wormhole traversing space into one traversing time by accelerating one of its two mouths. However, according to general relativity, it would not be possible to use a wormhole to travel back to a time earlier than when the wormhole was first converted into a time "machine". Until this time it could not have been noticed or have been used.

Raychaudhuri's theorem and exotic matter

To see why exotic matter is required, consider an incoming light front traveling along geodesics, which then crosses the wormhole and re-expands on the other side. The expansion goes from negative to positive. As the wormhole neck is of finite size, we would not expect caustics to develop, at least within the vicinity of the neck. According to the optical Raychaudhuri's theorem, this requires a violation of the averaged null energy condition. Quantum effects such as the Casimir effect cannot violate the averaged null energy condition in any neighborhood of space with zero curvature, but calculations in semiclassical gravity suggest that quantum effects may be able to violate this condition in curved spacetime. Although it was hoped recently that quantum effects could not violate an achronal version of the averaged null energy condition, violations have nevertheless been found, so it remains an open possibility that quantum effects might be used to support a wormhole.

Modified general relativity

In some hypotheses where general relativity is modified, it is possible to have a wormhole that does not collapse without having to resort to exotic matter. For example, this is possible with R gravity, a form of f(R) gravity.

Faster-than-light travel

Further information: Faster-than-light
Wormhole travel as envisioned by Les Bossinas for NASA Digital art by Les Bossinas (Cortez III Service Corp.), 1998
Wormhole travel as envisioned by Les Bossinas for NASA, c. 1998

The impossibility of faster-than-light relative speed applies only locally. Wormholes might allow effective superluminal (faster-than-light) travel by ensuring that the speed of light is not exceeded locally at any time. While traveling through a wormhole, subluminal (slower-than-light) speeds are used. If two points are connected by a wormhole whose length is shorter than the distance between them outside the wormhole, the time taken to traverse it could be less than the time it would take a light beam to make the journey if it took a path through the space outside the wormhole. However, a light beam traveling through the same wormhole would beat the traveler.

Time travel

Main article: Time travel

If traversable wormholes exist, they might allow time travel. A proposed time-travel machine using a traversable wormhole might hypothetically work in the following way: One end of the wormhole is accelerated to some significant fraction of the speed of light, perhaps with some advanced propulsion system, and then brought back to the point of origin. Alternatively, another way is to take one entrance of the wormhole and move it to within the gravitational field of an object that has higher gravity than the other entrance, and then return it to a position near the other entrance. For both these methods, time dilation causes the end of the wormhole that has been moved to have aged less, or become "younger", than the stationary end as seen by an external observer; however, time connects differently through the wormhole than outside it, so that synchronized clocks at either end of the wormhole will always remain synchronized as seen by an observer passing through the wormhole, no matter how the two ends move around. This means that an observer entering the "younger" end would exit the "older" end at a time when it was the same age as the "younger" end, effectively going back in time as seen by an observer from the outside. One significant limitation of such a time machine is that it is only possible to go as far back in time as the initial creation of the machine; it is more of a path through time rather than it is a device that itself moves through time, and it would not allow the technology itself to be moved backward in time.

According to current theories on the nature of wormholes, construction of a traversable wormhole would require the existence of a substance with negative energy, often referred to as "exotic matter". More technically, the wormhole spacetime requires a distribution of energy that violates various energy conditions, such as the null energy condition along with the weak, strong, and dominant energy conditions. However, it is known that quantum effects can lead to small measurable violations of the null energy condition, and many physicists believe that the required negative energy may actually be possible due to the Casimir effect in quantum physics. Although early calculations suggested a very large amount of negative energy would be required, later calculations showed that the amount of negative energy can be made arbitrarily small.

In 1993, Matt Visser argued that the two mouths of a wormhole with such an induced clock difference could not be brought together without inducing quantum field and gravitational effects that would either make the wormhole collapse or the two mouths repel each other, or otherwise prevent information from passing through the wormhole. Because of this, the two mouths could not be brought close enough for causality violation to take place. However, in a 1997 paper, Visser hypothesized that a complex "Roman ring" (named after Tom Roman) configuration of an N number of wormholes arranged in a symmetric polygon could still act as a time machine, although he concludes that this is more likely a flaw in classical quantum gravity theory rather than proof that causality violation is possible.

Interuniversal travel

See also: Multiverse

A possible resolution to the paradoxes resulting from wormhole-enabled time travel rests on the many-worlds interpretation of quantum mechanics.

In 1991 David Deutsch showed that quantum theory is fully consistent (in the sense that the so-called density matrix can be made free of discontinuities) in spacetimes with closed timelike curves. However, later it was shown that such a model of closed timelike curves can have internal inconsistencies as it will lead to strange phenomena like distinguishing non-orthogonal quantum states and distinguishing proper and improper mixture. Accordingly, the destructive positive feedback loop of virtual particles circulating through a wormhole time machine, a result indicated by semi-classical calculations, is averted. A particle returning from the future does not return to its universe of origination but to a parallel universe. This suggests that a wormhole time machine with an exceedingly short time jump is a theoretical bridge between contemporaneous parallel universes.

Because a wormhole time-machine introduces a type of nonlinearity into quantum theory, this sort of communication between parallel universes is consistent with Joseph Polchinski's proposal of an Everett phone (named after Hugh Everett) in Steven Weinberg's formulation of nonlinear quantum mechanics.

The possibility of communication between parallel universes has been dubbed interuniversal travel.

Wormhole can also be depicted in a Penrose diagram of a Schwarzschild black hole. In the Penrose diagram, an object traveling faster than light will cross the black hole and will emerge from another end into a different space, time or universe. This will be an inter-universal wormhole.

Metrics

Theories of wormhole metrics describe the spacetime geometry of a wormhole and serve as theoretical models for time travel. An example of a (traversable) wormhole metric is the following:

d s 2 = − c 2 d t 2 + d ℓ 2 + ( k 2 + ℓ 2 ) ( d θ 2 + sin 2 ⁡ θ d φ 2 ) , {\displaystyle ds^{2}=-c^{2}\,dt^{2}+d\ell ^{2}+(k^{2}+\ell ^{2})(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}),}

first presented by Ellis (see Ellis wormhole) as a special case of the Ellis drainhole.

One type of non-traversable wormhole metric is the Schwarzschild solution (see the first diagram):

d s 2 = − c 2 ( 1 − 2 G M r c 2 ) d t 2 + d r 2 1 − 2 G M r c 2 + r 2 ( d θ 2 + sin 2 ⁡ θ d φ 2 ) . {\displaystyle ds^{2}=-c^{2}\left(1-{\frac {2GM}{rc^{2}}}\right)\,dt^{2}+{\frac {dr^{2}}{1-{\frac {2GM}{rc^{2}}}}}+r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}).}

The original Einstein–Rosen bridge was described in an article published in July 1935.

For the Schwarzschild spherically symmetric static solution

d s 2 = − 1 1 − 2 m r d r 2 − r 2 ( d θ 2 + sin 2 ⁡ θ d φ 2 ) + ( 1 − 2 m r ) d t 2 , {\displaystyle ds^{2}=-{\frac {1}{1-{\frac {2m}{r}}}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}\right)\,dt^{2},}

where d s {\displaystyle ds} is the proper time and c = 1 {\displaystyle c=1} .

If one replaces r {\displaystyle r} with u {\displaystyle u} according to u 2 = r − 2 m {\displaystyle u^{2}=r-2m}

d s 2 = − 4 ( u 2 + 2 m ) d u 2 − ( u 2 + 2 m ) 2 ( d θ 2 + sin 2 ⁡ θ d φ 2 ) + u 2 u 2 + 2 m d t 2 {\displaystyle ds^{2}=-4(u^{2}+2m)\,du^{2}-(u^{2}+2m)^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+{\frac {u^{2}}{u^{2}+2m}}\,dt^{2}}

The four-dimensional space is described mathematically by two congruent parts or "sheets", corresponding to u > 0 {\displaystyle u>0} and u < 0 {\displaystyle u<0} , which are joined by a hyperplane r = 2 m {\displaystyle r=2m} or u = 0 {\displaystyle u=0} in which g {\displaystyle g} vanishes. We call such a connection between the two sheets a "bridge".

— A. Einstein, N. Rosen, "The Particle Problem in the General Theory of Relativity"

For the combined field, gravity and electricity, Einstein and Rosen derived the following Schwarzschild static spherically symmetric solution

φ 1 = φ 2 = φ 3 = 0 , φ 4 = ε 4 , {\displaystyle \varphi _{1}=\varphi _{2}=\varphi _{3}=0,\varphi _{4}={\frac {\varepsilon }{4}},} d s 2 = − 1 ( 1 − 2 m r − ε 2 2 r 2 ) d r 2 − r 2 ( d θ 2 + sin 2 ⁡ θ d φ 2 ) + ( 1 − 2 m r − ε 2 2 r 2 ) d t 2 , {\displaystyle ds^{2}=-{\frac {1}{\left(1-{\frac {2m}{r}}-{\frac {\varepsilon ^{2}}{2r^{2}}}\right)}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}-{\frac {\varepsilon ^{2}}{2r^{2}}}\right)\,dt^{2},}

where ε {\displaystyle \varepsilon } is the electric charge.

The field equations without denominators in the case when m = 0 {\displaystyle m=0} can be written

φ μ ν = φ μ , ν − φ ν , μ {\displaystyle \varphi _{\mu \nu }=\varphi _{\mu ,\nu }-\varphi _{\nu ,\mu }} g 2 φ μ ν ; σ g ν σ = 0 {\displaystyle g^{2}\varphi _{\mu \nu ;\sigma }g^{\nu \sigma }=0} g 2 ( R i k + φ i α φ k α − 1 4 g i k φ α β φ α β ) = 0 {\displaystyle g^{2}(R_{ik}+\varphi _{i\alpha }\varphi _{k}^{\alpha }-{\frac {1}{4}}g_{ik}\varphi _{\alpha \beta }\varphi ^{\alpha \beta })=0}

In order to eliminate singularities, if one replaces r {\displaystyle r} by u {\displaystyle u} according to the equation:

u 2 = r 2 − ε 2 2 {\displaystyle u^{2}=r^{2}-{\frac {\varepsilon ^{2}}{2}}}

and with m = 0 {\displaystyle m=0} one obtains

φ 1 = φ 2 = φ 3 = 0 {\displaystyle \varphi _{1}=\varphi _{2}=\varphi _{3}=0} and φ 4 = ε ( u 2 + ε 2 2 ) 1 / 2 {\displaystyle \varphi _{4}={\frac {\varepsilon }{\left(u^{2}+{\frac {\varepsilon ^{2}}{2}}\right)^{1/2}}}} d s 2 = − d u 2 − ( u 2 + ε 2 2 ) ( d θ 2 + sin 2 ⁡ θ d φ 2 ) + ( 2 u 2 2 u 2 + ε 2 ) d t 2 {\displaystyle ds^{2}=-du^{2}-\left(u^{2}+{\frac {\varepsilon ^{2}}{2}}\right)(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left({\frac {2u^{2}}{2u^{2}+\varepsilon ^{2}}}\right)\,dt^{2}}

The solution is free from singularities for all finite points in the space of the two sheets

— A. Einstein, N. Rosen, "The Particle Problem in the General Theory of Relativity"

In fiction

Main article: Wormholes in fiction

Wormholes are a common element in science fiction because they allow interstellar, intergalactic, and sometimes even interuniversal travel within human lifetime scales. In fiction, wormholes have also served as a method for time travel.

See also

Notes

  1. Other computer-rendered images and animations of traversable wormholes can be seen on this page by the creator of the image in the article, and this page has additional renderings.

References

Citations

  1. Overbye, Dennis (10 October 2022). "Black Holes May Hide a Mind-Bending Secret About Our Universe – Take gravity, add quantum mechanics, stir. What do you get? Just maybe, a holographic cosmos". The New York Times. Retrieved 10 October 2022.
  2. Shinkai, Hisa-aki; Torii, Takashi (2015-01-21). "Wormhole Dynamics". Journal of Physics: Conference Series. 574: 012056. doi:10.1088/1742-6596/574/1/012056. ISSN 1742-6588.
  3. Choi, Charles Q. (2013-12-03). "Spooky physics phenomenon may link universe's wormholes". NBC News. Retrieved 2019-07-30.
  4. Cramer, John; Forward, Robert; Morris, Michael; Visser, Matt; Benford, Gregory; Landis, Geoffrey (1995). "Natural wormholes as gravitational lenses". Physical Review D. 51 (6): 3117–3120. arXiv:astro-ph/9409051. Bibcode:1995PhRvD..51.3117C. doi:10.1103/PhysRevD.51.3117. PMID 10018782. S2CID 42837620.
  5. "Searching for a 'Subway to the Stars'" (Press release). Archived from the original on 2012-04-15.
  6. Thorne, Kip S. (1994). Black holes and time warps : Einstein's outrageous legacy. New York. p. 493. ISBN 978-0393312768.{{cite book}}: CS1 maint: location missing publisher (link)
  7. Weyl, H. (1921). "Feld und Materie". Annalen der Physik. 65 (14): 541–563. Bibcode:1921AnP...370..541W. doi:10.1002/andp.19213701405.
  8. Scholz, Erhard, ed. (2001). Hermann Weyl's Raum – Zeit – Materie and a General Introduction to His Scientific Work. Oberwolfach Seminars. Vol. 30. Springer. p. 199. ISBN 9783764364762.
  9. ^ "Hermann Weyl": entry in the Stanford Encyclopedia of Philosophy.
  10. Misner, C. W.; Wheeler, J. A. (1957). "Classical physics as geometry". Ann. Phys. 2 (6): 525. Bibcode:1957AnPhy...2..525M. doi:10.1016/0003-4916(57)90049-0.
  11. ^ Visser, Matt (1996). Lorentzian Wormholes. Springer-Verlag. ISBN 978-1-56396-653-8.
  12. ^ Rodrigo, Enrico (2010). The Physics of Stargates. Eridanus Press. p. 281. ISBN 978-0-9841500-0-7.
  13. "Microscopic wormholes possible in theory". phys.org. Retrieved 22 April 2021.
  14. Blázquez-Salcedo, Jose Luis; Knoll, Christian; Radu, Eugen (9 March 2021). "Traversable Wormholes in Einstein-Dirac-Maxwell Theory". Physical Review Letters. 126 (10): 101102. arXiv:2010.07317. Bibcode:2021PhRvL.126j1102B. doi:10.1103/PhysRevLett.126.101102. hdl:10773/32560. PMID 33784127. S2CID 222378921. Retrieved 22 April 2021.
  15. Konoplya, R. A.; Zhidenko, A. (4 March 2022). "Traversable Wormholes in General Relativity". Physical Review Letters. 128 (9): 091104. arXiv:2106.05034. Bibcode:2022PhRvL.128i1104K. doi:10.1103/PhysRevLett.128.091104. PMID 35302821. S2CID 247245028.
  16. Schirber, Michael (9 March 2021). "Wormholes Open for Transport". Physics. Retrieved 22 April 2021.
  17. Maldacena, Juan; Milekhin, Alexey (9 March 2021). "Humanly traversable wormholes". Physical Review D. 103 (6): 066007. arXiv:2008.06618. Bibcode:2021PhRvD.103f6007M. doi:10.1103/PhysRevD.103.066007. Available under CC BY 4.0.
  18. Vladimir Dobrev (ed.), Lie Theory and Its Applications in Physics: Varna, Bulgaria, June 2015, Springer, 2016, p. 246.
  19. ^ A. Einstein and N. Rosen, "The Particle Problem in the General Theory of Relativity," Phys. Rev. 48(73) (1935).
  20. "Black Holes Explained – From Birth to Death". YouTube. Archived from the original on 2021-12-11.
  21. "Collapse to a Black Hole". Casa.colorado.edu. 2010-10-03. Retrieved 2010-11-11. This tertiary source reuses information from other sources but does not name them.
  22. Flamm (1916). "Beiträge zur Einsteinschen Gravitationstheorie". Physikalische Zeitschrift. XVII: 448. ("Comments on Einstein's Theory of Gravity")
  23. Lindley, David (Mar 25, 2005). "Focus: The Birth of Wormholes". Physics. 15. American Physical Society. Retrieved 20 February 2016.
  24. Fuller, Robert W.; Wheeler, John A. (1962-10-15). "Causality and Multiply Connected Space-Time". Physical Review. 128 (2). American Physical Society (APS): 919–929. Bibcode:1962PhRv..128..919F. doi:10.1103/physrev.128.919. ISSN 0031-899X.
  25. Poplawski, Nikodem J. (2010). "Cosmology with torsion: An alternative to cosmic inflation". Phys. Lett. B. 694 (3): 181–185. arXiv:1007.0587. Bibcode:2010PhLB..694..181P. doi:10.1016/j.physletb.2010.09.056.
  26. Thorne, Kip S. (1994). Black holes and time warps : Einstein's outrageous legacy. New York. p. 488. ISBN 978-0393312768.{{cite book}}: CS1 maint: location missing publisher (link)
  27. J. Wheeler (1957). "On the nature of quantum geometrodynamics". Ann. Phys. 2 (6): 604–614. Bibcode:1957AnPhy...2..604W. doi:10.1016/0003-4916(57)90050-7. (A follow-up paper to Misner and Wheeler (December 1957).)
  28. Eduard Prugovecki, Quantum Geometry: A Framework for Quantum General Relativity, Springer, 2013, p. 412.
  29. Everett, Allen; Roman, Thomas (2012). Time Travel and Warp Drives. University of Chicago Press. p. 167. ISBN 978-0-226-22498-5.
  30. "Space and Time Warps". Hawking.org.uk. Archived from the original on 2012-02-10. Retrieved 2010-11-11.
  31. ^ Morris, Michael; Thorne, Kip; Yurtsever, Ulvi (1988). "Wormholes, Time Machines, and the Weak Energy Condition" (PDF). Physical Review Letters. 61 (13): 1446–1449. Bibcode:1988PhRvL..61.1446M. doi:10.1103/PhysRevLett.61.1446. PMID 10038800.
  32. Sopova; Ford (2002). "The Energy Density in the Casimir Effect". Physical Review D. 66 (4): 045026. arXiv:quant-ph/0204125. Bibcode:2002PhRvD..66d5026S. CiteSeerX 10.1.1.251.7471. doi:10.1103/PhysRevD.66.045026. S2CID 10649139.
  33. Ford; Roman (1995). "Averaged Energy Conditions and Quantum Inequalities". Physical Review D. 51 (8): 4277–4286. arXiv:gr-qc/9410043. Bibcode:1995PhRvD..51.4277F. doi:10.1103/PhysRevD.51.4277. PMID 10018903. S2CID 7413835.
  34. Olum (1998). "Superluminal travel requires negative energies". Physical Review Letters. 81 (17): 3567–3570. arXiv:gr-qc/9805003. Bibcode:1998PhRvL..81.3567O. doi:10.1103/PhysRevLett.81.3567. S2CID 14513456.
  35. "Newfound Wormhole Allows Information to Escape Black Holes". Quanta Magazine. 23 October 2017.
  36. ^ Thorne, Kip S. (1994). Black Holes and Time Warps. W. W. Norton. ISBN 978-0-393-31276-8.
  37. Ian H., Redmount; Wai-Mo Suen (1994). "Quantum Dynamics of Lorentzian Spacetime Foam". Physical Review D. 49 (10): 5199–5210. arXiv:gr-qc/9309017. Bibcode:1994PhRvD..49.5199R. doi:10.1103/PhysRevD.49.5199. PMID 10016836. S2CID 39296197.
  38. Kirillov, A. A.; P. Savelova, E. (2008). "Dark Matter from a gas of wormholes". Physics Letters B. 660 (3): 93–99. arXiv:0707.1081. Bibcode:2008PhLB..660...93K. doi:10.1016/j.physletb.2007.12.034. S2CID 12150385.
  39. Rodrigo, Enrico (2009). "Denouement of a Wormhole-Brane Encounter". International Journal of Modern Physics D. 18 (12): 1809–1819. arXiv:0908.2651. Bibcode:2009IJMPD..18.1809R. doi:10.1142/S0218271809015333. S2CID 119239038.
  40. ^ John G. Cramer; Robert L. Forward; Michael S. Morris; Matt Visser; Gregory Benford & Geoffrey A. Landis (1995). "Natural Wormholes as Gravitational Lenses". Physical Review D. 51 (6): 3117–3120. arXiv:astro-ph/9409051. Bibcode:1995PhRvD..51.3117C. doi:10.1103/PhysRevD.51.3117. PMID 10018782. S2CID 42837620.
  41. H. G. Ellis (1973). "Ether flow through a drainhole: A particle model in general relativity". Journal of Mathematical Physics. 14 (1): 104–118. Bibcode:1973JMP....14..104E. doi:10.1063/1.1666161.
  42. K. A. Bronnikov (1973). "Scalar-tensor theory and scalar charge". Acta Physica Polonica. B4: 251–266.
  43. Morris, Michael S. & Thorne, Kip S. (1988). "Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity". American Journal of Physics. 56 (5): 395–412. Bibcode:1988AmJPh..56..395M. doi:10.1119/1.15620.
  44. Elias Gravanis; Steven Willison (2007). "'Mass without mass' from thin shells in Gauss-Bonnet gravity". Phys. Rev. D. 75 (8): 084025. arXiv:gr-qc/0701152. Bibcode:2007PhRvD..75h4025G. doi:10.1103/PhysRevD.75.084025. S2CID 53529713.
  45. Fewster, Christopher J.; Ken D. Olum; Michael J. Pfenning (2007). "Averaged null energy condition in spacetimes with boundaries". Physical Review D. 75 (2): 025007. arXiv:gr-qc/0609007. Bibcode:2007PhRvD..75b5007F. doi:10.1103/PhysRevD.75.025007. S2CID 119726654.
  46. Visser, Matt (1996). "Gravitational vacuum polarization. II. Energy conditions in the Boulware vacuum". Physical Review D. 54 (8): 5116–5122. arXiv:gr-qc/9604008. Bibcode:1996PhRvD..54.5116V. doi:10.1103/PhysRevD.54.5116. PMID 10021199. S2CID 31954680.
  47. Graham, Noah; Ken D. Olum (2007). "Achronal averaged null energy condition". Physical Review D. 76 (6): 064001. arXiv:0705.3193. Bibcode:2007PhRvD..76f4001G. doi:10.1103/PhysRevD.76.064001. S2CID 119285639.
  48. Urban, Douglas; Ken D. Olum (2010). "Spacetime averaged null energy condition". Physical Review D. 81 (6): 124004. arXiv:1002.4689. Bibcode:2010PhRvD..81l4004U. doi:10.1103/PhysRevD.81.124004. S2CID 118312373.
  49. Duplessis, Francis; Easson, Damien A. (2015). "Exotica ex nihilo: Traversable wormholes & non-singular black holes from the vacuum of quadratic gravity". Physical Review D. 92 (4): 043516. arXiv:1506.00988. Bibcode:2015PhRvD..92d3516D. doi:10.1103/PhysRevD.92.043516. S2CID 118307327.
  50. Susskind, Leonard (2005). "Wormholes and Time Travel? Not Likely". arXiv:gr-qc/0503097.
  51. Everett, Allen; Roman, Thomas (2012). Time Travel and Warp Drives. University of Chicago Press. p. 135. ISBN 978-0-226-22498-5.
  52. Cramer, John G. (1994). "NASA Goes FTL Part 1: Wormhole Physics". Analog Science Fiction & Fact Magazine. Archived from the original on June 27, 2006. Retrieved December 2, 2006.
  53. Visser, Matt; Sayan Kar; Naresh Dadhich (2003). "Traversable wormholes with arbitrarily small energy condition violations". Physical Review Letters. 90 (20): 201102.1 – 201102.4. arXiv:gr-qc/0301003. Bibcode:2003PhRvL..90t1102V. doi:10.1103/PhysRevLett.90.201102. PMID 12785880. S2CID 8813962.
  54. Visser, Matt (1993). "From wormhole to time machine: Comments on Hawking's Chronology Protection Conjecture". Physical Review D. 47 (2): 554–565. arXiv:hep-th/9202090. Bibcode:1993PhRvD..47..554V. doi:10.1103/PhysRevD.47.554. PMID 10015609. S2CID 16830951.
  55. Visser, Matt (2002). The quantum physics of chronology protection. arXiv:gr-qc/0204022. Bibcode:2003ftpc.book..161V.
  56. Visser, Matt (1997). "Traversable wormholes: the Roman ring". Physical Review D. 55 (8): 5212–5214. arXiv:gr-qc/9702043. Bibcode:1997PhRvD..55.5212V. doi:10.1103/PhysRevD.55.5212. S2CID 2869291.
  57. Deutsch, David (1991). "Quantum Mechanics Near Closed Timelike Lines". Physical Review D. 44 (10): 3197–3217. Bibcode:1991PhRvD..44.3197D. doi:10.1103/PhysRevD.44.3197. PMID 10013776.
  58. Brun; et al. (2009). "Localized Closed Timelike Curves Can Perfectly Distinguish Quantum States". Physical Review Letters. 102 (21): 210402. arXiv:0811.1209. Bibcode:2009PhRvL.102u0402B. doi:10.1103/PhysRevLett.102.210402. PMID 19519086. S2CID 35370109.
  59. Pati; Chakrabarty; Agrawal (2011). "Purification of mixed states with closed timelike curve is not possible". Physical Review A. 84 (6): 062325. arXiv:1003.4221. Bibcode:2011PhRvA..84f2325P. doi:10.1103/PhysRevA.84.062325. S2CID 119292717.
  60. Polchinski, Joseph (1991). "Weinberg's Nonlinear quantum Mechanics and the Einstein–Podolsky–Rosen Paradox". Physical Review Letters. 66 (4): 397–400. Bibcode:1991PhRvL..66..397P. doi:10.1103/PhysRevLett.66.397. PMID 10043797.
  61. Enrico Rodrigo, The Physics of Stargates: Parallel Universes, Time Travel, and the Enigma of Wormhole Physics, Eridanus Press, 2010, p. 281.
  62. Samuel Walker, "Inter-universal travel: I wouldn't start from here, New Scientist (1 February 2017).
  63. Raine, Derek; Thomas, Edwin (2009). Black Holes: An Introduction (2nd ed.). Imperial College Press. p. 143. doi:10.1142/p637. ISBN 978-1-84816-383-6.
  64. Einstein, A.; Rosen, N. (1 July 1935). "The Particle Problem in the General Theory of Relativity". Physical Review. 48 (1): 73–77. Bibcode:1935PhRv...48...73E. doi:10.1103/PhysRev.48.73.
  65. "Leonard Susskind | "ER = EPR" or "What's Behind the Horizons of Black Holes?"". Archived from the original on 2021-12-11 – via www.youtube.com.
  66. "Magnetic 'wormhole' connecting two regions of space created for the first time". ScienceDaily.
  67. "Magnetic wormhole created for first time". UAB Barcelona.

Sources

External links

Black holes
Types
Size
Formation
Properties
Issues
Metrics
Alternatives
Analogs
Lists
Related
Notable
Time travel
General terms and concepts
Time travel in fiction
Temporal paradoxes
Parallel timelines
Philosophy of space and time
Spacetimes in general relativity that
can contain closed timelike curves
Categories: