| Set of gyroelongated cupolae | |
|---|---|
 Example pentagonal form | |
| Faces | 3n triangles n squares 1 n-gon 1 2n-gon |
| Edges | 9n |
| Vertices | 5n |
| Symmetry group | Cnv, , (*nn) |
| Rotational group | Cn, , (nn) |
| Dual polyhedron | |
| Properties | convex |
In geometry, the gyroelongated cupolae are an infinite set of polyhedra, constructed by adjoining an n-gonal cupola to an 2n-gonal antiprism.
There are three gyroelongated cupolae that are Johnson solids made from regular triangles and square, and pentagons. Higher forms can be constructed with isosceles triangles. Adjoining a triangular prism to a square antiprism also generates a polyhedron, but has adjacent parallel faces, so is not a Johnson solid. The hexagonal form can be constructed from regular polygons, but the cupola faces are all in the same plane. Topologically other forms can be constructed without regular faces.
Forms
| name | faces | |
|---|---|---|
 |
gyroelongated digonal cupola | 2+8 triangles, 2+1 square |
 |
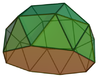
gyroelongated triangular cupola (J22) | 9+1 triangles, 3 squares, 1 hexagon |
 |
gyroelongated square cupola (J23) | 12 triangles, 4+1 squares, 1 octagon |
 |
gyroelongated pentagonal cupola (J24) | 15 triangles, 5 squares, 1 pentagon, 1 decagon |
| gyroelongated hexagonal cupola | 18 triangles, 6 squares, 1 hexagon, 1 dodecagon |
See also
References
- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
| Convex polyhedra | |||||
|---|---|---|---|---|---|
| Platonic solids (regular) | |||||
| Archimedean solids (semiregular or uniform) | |||||
| Catalan solids (duals of Archimedean) |
| ||||
| Dihedral regular | |||||
| Dihedral uniform |
| ||||
| Dihedral others | |||||
| Degenerate polyhedra are in italics. | |||||
This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it. |