Misplaced Pages

A nanophotonic resonator or nanocavity is an optical cavity which is on the order of tens to hundreds of nanometers in size. Optical cavities are a major component of all lasers, they are responsible for providing amplification of a light source via positive feedback, a process known as amplified spontaneous emission or ASE. Nanophotonic resonators offer inherently higher light energy confinement than ordinary cavities, which means stronger light-material interactions, and therefore lower lasing threshold provided the quality factor of the resonator is high. Nanophotonic resonators can be made with photonic crystals, silicon, diamond, or metals such as gold.

For a laser in a nanocavity, spontaneous emission (SE) from the gain medium is enhanced by the Purcell effect, equal to the quality factor or ${\displaystyle Q}$-factor of the cavity divided by the effective mode field volume, ${\displaystyle F=Q/V_{\text{mode}}}$. Therefore, reducing the volume of an optical cavity can dramatically increase this factor, which can have the effect of decreasing the input power threshold for lasing. This also means that the response time of spontaneous emission from a gain medium in a nanocavity also decreases, the result being that the laser may reach lasing steady state picoseconds after it starts being pumped. A laser formed in a nanocavity therefore may be modulated via its pump source at very high speeds. Spontaneous emission rate increases of over 70 times modern semiconductor laser devices have been demonstrated, with theoretical laser modulation speeds exceeding 100 GHz, an order of magnitude higher than modern semiconductor lasers, and higher than most digital oscilloscopes. Nanophotonic resonators have also been applied to create nanoscale filters and photonic chips

Differences from classical cavities

For cavities much larger than the wavelength of the light they contain, cavities with very high Q factors have already been realized (~125,000,000). However, high ${\displaystyle Q}$ cavities on the order of the same size as the optical wavelength have been difficult to produce due to the inverse relationship between radiation losses and cavity size. When dealing with a cavity much larger than the optical wavelength, it is simple to design interfaces such that light ray paths fulfill total internal reflection conditions or Bragg reflection conditions. For light confined within much smaller cavities near the size of the optical wavelength, deviations from ray optics approximations become severe and it becomes infeasible, if not impossible to design a cavity which fulfills optimum reflection conditions for all three spatial components of the propagating light wave vectors.

In a laser, the gain medium emits light randomly in all directions. With a classical cavity, the number of photons which are coupled into a single cavity mode relative to the total number of spontaneously emitted photons is relatively low because of the geometric inefficiency of the cavity, described by the Purcell factor ${\displaystyle Q/V_{\text{mode}}}$. The rate at which lasing in such a cavity can be modulated depends on the relaxation frequency of the resonator described by equation 1.

${\displaystyle R_{2}=(av_{g}P_{0})/\tau _{p}+\beta /(\tau _{p}\tau _{r0}/F)+(\beta N_{0})/((\tau _{r0}/F)P_{0})(1/\tau _{\text{total}}-1/(\tau _{r0}/F))\,\,\,\,\,\,\,\,(1)}$

Where ${\displaystyle \tau _{r0}}$ is the intrinsic carrier radiative lifetime of the bulk material, ${\displaystyle a}$ is the differential gain, ${\displaystyle v_{g}}$ is the group velocity, ${\displaystyle \tau _{p}=Q/\omega _{L}}$ is the photon lifetime, ${\displaystyle \omega _{L}}$ is the lasing frequency, ${\displaystyle \beta }$ is the spontaneous emission coupling factor which is enhanced by the Purcell effect, and ${\displaystyle 1/\tau _{\text{total}}=F/\tau _{r_{0}}+1/\tau _{nr}}$ where ${\displaystyle \tau _{nr}}$ is the non-radiative lifetime. In the case of minimal Purcell effect in a classical cavity with small ${\displaystyle F=Q/V_{\text{mode}}}$, only the first term of equation 1 is considered, and the only way to increase modulation frequency is to increase photon density ${\displaystyle P_{0}}$ by increasing the pumping power. However, thermal effects practically limit the modulation frequency to around 20 GHz, making this approach is inefficient.

In nanoscale photonic resonators with high ${\displaystyle Q}$, the effective mode volume ${\displaystyle V_{\text{mode}}}$ is inherently very small resulting in high ${\displaystyle F}$ and ${\displaystyle \beta }$, and terms 2 and 3 in equation 1 are no longer negligible. Consequently, nanocavities are fundamentally better suited to efficiently produce spontaneous emission and amplified spontaneous emission light modulated at frequencies much higher than 20 GHz without negative thermal effects.

Materials and designs

Nanocavities made from photonic crystals are typically implemented in a photonic crystal slab structure. Such a slab will generally have a periodic lattice structure of physical holes in the material. For light propagating within the slab, a reflective interface is formed at these holes due to the periodic differences in refractive index in the structure.

A common photonic crystal nanocavity design shown is essentially a photonic crystal with an intentional defect (holes missing). This structure having periodic changes in refractive index on the order of the length of the optical wavelength satisfies Bragg reflection conditions in the ${\displaystyle y}$ and ${\displaystyle z}$ directions for a particular wavelength range, and the slab boundaries in the ${\displaystyle x}$ direction create another reflective boundary due to oblique reflection at dielectric boundaries. This results in theoretically perfect wave confinement in the ${\displaystyle y}$ and ${\displaystyle z}$ directions along the axis of a lattice row, and good confinement along the ${\displaystyle x}$ direction. Since this confinement effect along the ${\displaystyle y}$ and ${\displaystyle z}$ directions (directions of the crystal lattice) is only for a range of frequencies, it has been referred to as a photonic bandgap, since there is a discrete set of photon energies which cannot propagate in the lattice directions in the material. However, because of the diffraction of waves propagating inside this structure, radiation energy does escape the cavity within the photonic crystal slab plane. The lattice spacing can be tuned to produce optimal boundary conditions of the standing wave inside the cavity to produce minimal loss and highest ${\displaystyle Q}$. Beside those conventional resonators, they are some examples of rewritable and/or movable cavities, which are accomplished by a micro infiltration system and by a manipulation of single nanoparticles inside photonic crystals.

Metals can also be an effective way to confine light in structures equal to or smaller than the optical wavelength. This effect is emergent from the confined surface plasmon resonance induced by the resonating light, which, when confined to the surface of a nanostructure such as a gold channel or nanorod, induces electromagnetic resonance. Surface plasmon effects are strong in the visible range because the permittivity of a metal is very large and negative at visible frequencies. At frequencies higher than the visible range, the permittivity of a metal is closer to zero, and the metal stops being useful for focussing electric and magnetic fields. This effect was originally observed in radio and microwave engineering, where metal antennas and waveguides may be hundreds of times smaller than the free-space wavelength. In the same way, visible light can be constricted to the nano level with metal structures which form channels, tips, gaps, etc. Gold is also a convenient choice for nanofabrication because of its unreactivity and ease of use with chemical vapour deposition.

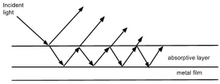
A planar nanocavity consists of an absorptive semiconductive film no more than a few nanometers thick over a metal film also a few nanometers thick. Incident light is absorbed and reflected off of both layers, the absorbed light then resonates between the two interfaces, transmitting some light back at after each cycle. Germanium is commonly used for the absorptive layer, while gold, aluminum, and aluminum oxide are used as alternatives as well. Planar nanocavities are commonly used for thin film interference, which occurs when incident light waves reflected by the upper and lower boundaries of a thin film interfere with one another forming a new wave. An example of this is the colorful patterns produced by thin layers of oil on a surface. The difference in colors is due to minute differences in the distance reflected light travels whether it reflects from the top or bottom boundary of the oil layer. This difference is called the optical path difference, the difference in distance between the top and bottom reflection paths, which can be calculated with equation 2:

${\displaystyle {\text{OPD}}=2nd\,{\text{cos}}(\theta )\,\,\,\,\,\,\,\,(2)}$

${\displaystyle {\text{OPD}}=m\lambda \,\,\,\,\,\,\,\,(3)}$

Where ${\displaystyle n}$ is the refractive index of the absorptive material, ${\displaystyle d}$ is the thickness of the absorptive film, and ${\displaystyle \theta }$ is the angle of reflection. As expressed in the equation 3, the optical path length difference (OPD) can be related to wavelengths which constructively interfere in the thin film. As a result, light which enters the film at different angles interferes with itself varying amounts, produces an intensity gradient for narrowband light, and a spectrum gradient for white light.

Examples/applications

Nanophotonic circuit designs are similar in appearance to microwave and radio circuits, minimized by a factor of 100,000 or more. Researchers have made nano-optical antennas which emulate the design and functionality of radio antennas. There are a number of important differences between nanophotonics and scaled down microwave circuits. At optical frequency, metals behave much less like ideal conductors, and also exhibit plasmon-related effects like kinetic inductance and surface plasmon resonance. A nantenna is a nanoscopic rectifying antenna, a technology being developed to convert light into electric power. The concept is based on the rectenna which is used in wireless power transmission. A rectenna functions like a specialized radio antenna which is used to convert radio waves into direct current electricity. Light is composed of electromagnetic waves like radio waves, but of a much smaller wavelength. A nantenna, an application of a nanophotonic resonator, is a nanoscale rectenna on the order of the optical wavelength size, which acts as an "antenna" for light, converting light into electricity. Arrays of nantennas could be an efficient means of converting sunlight into electric power, producing solar energy more efficiently than semiconductor bandgap solar cells.

It has been suggested that nanophotonic resonators be used on multi core chips to both decrease size and boost efficiency. This is done by creating arrays of nanophotonic optical ring resonators that can transmit specific wavelengths of light between each other. Another use of nanophotonic resonators in computers is in optical RAM (O-RAM). O-Ram uses photonic crystal slab structure with properties such as strong confinement of photons and carriers to replace the functions of electrical circuits. The use of optical signals versus electrical signals is a 66.7% decrease in power consumption. Researchers have developed planar nanocavities that can reach 90% peak absorption using interference effects. This result is useful in that there are numerous applications that can benefit from these findings, specifically in energy conversion

References

1. ^ Akahane, Yoshihiro; Asano, Takashi; Song, Bong-Shik; Noda, Susumu (2003). "High-Q photonic nanocavity in a two-dimensional photonic crystal". Nature. 425 (6961). Springer Science and Business Media LLC: 944–947. Bibcode:2003Natur.425..944A. doi:10.1038/nature02063. ISSN 0028-0836. PMID 14586465. S2CID 4415688.
2. ^ Altug, Hatice; Englund, Dirk; Vučković, Jelena (2006). "Ultrafast photonic crystal nanocavity laser". Nature Physics. 2 (7). Springer Science and Business Media LLC: 484–488. Bibcode:2006NatPh...2..484A. CiteSeerX 10.1.1.162.2125. doi:10.1038/nphys343. ISSN 1745-2473.
3. Purcell, E. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69, 681 (1946).
4. Painter, O. (1999-06-11). "Two-Dimensional Photonic Band-Gap Defect Mode Laser". Science. 284 (5421). American Association for the Advancement of Science (AAAS): 1819–1821. doi:10.1126/science.284.5421.1819. ISSN 0036-8075. PMID 10364550. S2CID 6627734.
5. Lončar, Marko; Yoshie, Tomoyuki; Scherer, Axel; Gogna, Pawan; Qiu, Yueming (2002-10-07). "Low-threshold photonic crystal laser" (PDF). Applied Physics Letters. 81 (15). AIP Publishing: 2680–2682. Bibcode:2002ApPhL..81.2680L. doi:10.1063/1.1511538. ISSN 0003-6951.
6. ^ Noda, Susumu; Chutinan, Alongkarn; Imada, Masahiro (2000). "Trapping and emission of photons by a single defect in a photonic bandgap structure". Nature. 407 (6804). Springer Science and Business Media LLC: 608–610. Bibcode:2000Natur.407..608N. doi:10.1038/35036532. ISSN 0028-0836. PMID 11034204. S2CID 4380581.
7. ^ Song, B.-S. (2003-06-06). "Photonic Devices Based on In-Plane Hetero Photonic Crystals". Science. 300 (5625). American Association for the Advancement of Science (AAAS): 1537. doi:10.1126/science.1083066. ISSN 0036-8075. PMID 12791984. S2CID 7647042.
8. Armani, D. K.; Kippenberg, T. J.; Spillane, S. M.; Vahala, K. J. (2003). "Ultra-high-Q toroid microcavity on a chip". Nature. 421 (6926). Springer Science and Business Media LLC: 925–928. Bibcode:2003Natur.421..925A. doi:10.1038/nature01371. ISSN 0028-0836. PMID 12606995. S2CID 4420078.
9. Bayn, Igal; Salzman, Joseph (2008-03-27). "Ultra high-Q photonic crystal nanocavity design: The effect of a low-ε slab material". Optics Express. 16 (7). The Optical Society: 4972–4980. arXiv:0802.3342. Bibcode:2008OExpr..16.4972B. doi:10.1364/oe.16.004972. ISSN 1094-4087. PMID 18542597.
10. Coldren, L. A. & Corzine, S. W. Diode Lasers and Photonic Integrated Circuits (Wiley, New York, 1995).
11. Lear, K. L. et al. Small and large signal modulation of 850 nm oxide-confined vertical-cavity surface-emitting lasers. Advances in Vertical Cavity Surface Emitting Lasers in Trends in Optics and Photonics Series 15, 69–74 (1997).
12. Yamamoto, Y.; Machida, S.; Björk, G. (1991-07-01). "Microcavity semiconductor laser with enhanced spontaneous emission". Physical Review A. 44 (1). American Physical Society (APS): 657–668. Bibcode:1991PhRvA..44..657Y. doi:10.1103/physreva.44.657. ISSN 1050-2947. PMID 9905716.
13. Intonti, F; Vignolini, S; Türck, V; Colocci, M; Bettotti, P; Pavesi, L; Schweizer, S. L; Wehrspohn, R; Wiersma, D (2006). "Rewritable photonic circuits". Appl. Phys. Lett. 89 (21): 211117. Bibcode:2006ApPhL..89u1117I. doi:10.1063/1.2392720. S2CID 120516583.
14. Descharmes, N; Ulagalandha, P. D; Diao, Z; Tonin, M; Houdré, R (2013). "Observation of Backaction and Self-Induced Trapping in a Planar Hollow Photonic Crystal Cavity". Phys. Rev. Lett. 110 (12): 123601. Bibcode:2013PhRvL.110l3601D. doi:10.1103/PhysRevLett.110.123601. PMID 25166804.
15. Birowosuto, M. D; Yokoo, A; Zhang, G; Tateno, K; Kuramochi, E; Taniyama, H; Notomi, M (2014). "Movable high-Q nanoresonators realized by semiconductor nanowires on a Si photonic crystal platform". Nature Materials. 13 (1): 279–285. arXiv:1403.4237. Bibcode:2014NatMa..13..279B. doi:10.1038/nmat3873. PMID 24553654. S2CID 21333714.
16. ^ Falkovsky, L. A. (2008, October). Optical properties of graphene. In Journal of Physics: Conference Series (Vol. 129, No. 1, p. 012004). IOP Publishing.
17. Kerman, Andrew J.; Dauler, Eric A.; Keicher, William E.; Yang, Joel K. W.; Berggren, Karl K.; Gol’tsman, G.; Voronov, B. (2006-03-13). "Kinetic-inductance-limited reset time of superconducting nanowire photon counters". Applied Physics Letters. 88 (11). AIP Publishing: 111116. arXiv:physics/0510238. Bibcode:2006ApPhL..88k1116K. doi:10.1063/1.2183810. ISSN 0003-6951. S2CID 53373647.
18. ^ Okumura, Mitsutaka; Nakamura, Shyunichi; Tsubota, Susumu; Nakamura, Toshiko; Azuma, Masashi; Haruta, Masatake (1998). "Chemical vapor deposition of gold on Al₂O₃, SiO₂, and TiO₂ for the oxidation of CO and of H₂". Catalysis Letters. 51 (1/2). Springer Science and Business Media LLC: 53–58. doi:10.1023/a:1019020614336. ISSN 1011-372X. S2CID 92727508.
19. Gagliardi, R. M., & Karp, S. (1976). Optical communications. New York, Wiley-Interscience, 1976. 445 p., 1.
20. ^ Kotter, D. K., Novack, S. D., Slafer, W. D., & Pinhero, P. (2008, January). Solar nantenna electromagnetic collectors. In ASME 2008 2nd International Conference on Energy Sustainability collocated with the Heat Transfer, Fluids Engineering, and 3rd Energy Nanotechnology Conferences (pp. 409-415). American Society of Mechanical Engineers.
21. Zhou, Linjie; Djordjevic, Stevan S.; Proietti, Roberto; Ding, Dan; Yoo, S. J. B.; Amirtharajah, Rajeevan; Akella, Venkatesh (2009-02-20). "Design and evaluation of an arbitration-free passive optical crossbar for on-chip interconnection networks". Applied Physics A. 95 (4). Springer Science and Business Media LLC: 1111–1118. Bibcode:2009ApPhA..95.1111Z. doi:10.1007/s00339-009-5121-6. ISSN 0947-8396.
22. Nozaki, Kengo; Shinya, Akihiko; Matsuo, Shinji; Suzaki, Yasumasa; Segawa, Toru; et al. (2012-02-26). "Ultralow-power all-optical RAM based on nanocavities". Nature Photonics. 6 (4). Springer Science and Business Media LLC: 248–252. Bibcode:2012NaPho...6..248N. doi:10.1038/nphoton.2012.2. ISSN 1749-4885. S2CID 120061577.

• Optical components
• Laser science
• Photonics
• Resonators
• Nanotechnology