Misplaced Pages

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "5-cell" – news · newspapers · books · scholar · JSTOR (August 2024) (Learn how and when to remove this message)

This article may contain an excessive amount of intricate detail that may interest only a particular audience. Please help by spinning off or relocating any relevant information, and removing excessive detail that may be against Misplaced Pages's inclusion policy. (August 2024) (Learn how and when to remove this message)

5-cell (4-simplex)
A 3D orthogonal projection of a 5-cell performing a simple rotation
Type	Convex regular 4-polytope
Schläfli symbol	{3,3,3}
Coxeter diagram
Cells	5 {3,3}
Faces	10 {3}
Edges	10
Vertices	5
Vertex figure	(tetrahedron)
Petrie polygon	pentagon
Coxeter group	A4,
Dual	Self-dual
Properties	convex, isogonal, isotoxal, isohedral
Uniform index	1

In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol {3,3,3}. It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C₅, hypertetrahedron, 'pentachoron, pentatope, pentahedroid, tetrahedral pyramid, or 4-simplex (Coxeter's ${\displaystyle \alpha _{4}}$ polytope), the simplest possible convex 4-polytope, and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The 5-cell is a 4-dimensional pyramid with a tetrahedral base and four tetrahedral sides.

The regular 5-cell is bounded by five regular tetrahedra, and is one of the six regular convex 4-polytopes (the four-dimensional analogues of the Platonic solids). A regular 5-cell can be constructed from a regular tetrahedron by adding a fifth vertex one edge length distant from all the vertices of the tetrahedron. This cannot be done in 3-dimensional space. The regular 5-cell is a solution to the problem: Make 10 equilateral triangles, all of the same size, using 10 matchsticks, where each side of every triangle is exactly one matchstick, and none of the triangles and matchsticks intersect one another. No solution exists in three dimensions.

Properties

The 5-cell is the 4-dimensional simplex, the simplest possible 4-polytope. In other words, the 5-cell is a polychoron analogous to a tetrahedron in high dimension. It is formed by any five points which are not all in the same hyperplane (as a tetrahedron is formed by any four points which are not all in the same plane, and a triangle is formed by any three points which are not all in the same line). Any such five points constitute a 5-cell, though not usually a regular 5-cell. The regular 5-cell is not found within any of the other regular convex 4-polytopes except one: the 600-vertex 120-cell is a compound of 120 regular 5-cells.

The 5-cell is self-dual, meaning its dual polytope is 5-cell itself. Its maximal intersection with 3-dimensional space is the triangular prism. Its dichoral angle is ${\textstyle \arccos(-1/4)\approx 75.52^{\circ }}$.

It is the first in the sequence of 6 convex regular 4-polytopes, in order of volume at a given radius or number of vertexes.

The convex hull of two 5-cells in dual configuration is the disphenoidal 30-cell, dual of the bitruncated 5-cell.

As a configuration

This configuration matrix represents the 5-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 5-cell. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual polytope's matrix is identical to its 180 degree rotation. The k-faces can be read as rows left of the diagonal, while the k-figures are read as rows after the diagonal.

Element	k-face	fk	f0	f1	f2	f3	k-figs
	( )	f0	5	4	6	4	{3,3}
	{ }	f1	2	10	3	3	{3}
	{3}	f2	3	3	10	2	{ }
	{3,3}	f3	4	6	4	5	( )

All these elements of the 5-cell are enumerated in Branko Grünbaum's Venn diagram of 5 points, which is literally an illustration of the regular 5-cell in projection to the plane.

Geodesics and rotations

The 5-cell has only digon central planes through vertices. It has 10 digon central planes, where each vertex pair is an edge, not an axis, of the 5-cell. Each digon plane is orthogonal to 3 others, but completely orthogonal to none of them. The characteristic isoclinic rotation of the 5-cell has, as pairs of invariant planes, those 10 digon planes and their completely orthogonal central planes, which are 0-gon planes which intersect no 5-cell vertices.

There are only two ways to make a circuit of the 5-cell through all 5 vertices along 5 edges, so there are two discrete Hopf fibrations of the great digons of the 5-cell. Each of the two fibrations corresponds to a left-right pair of isoclinic rotations which each rotate all 5 vertices in a circuit of period 5. The 5-cell has only two distinct period 5 isoclines (those circles through all 5 vertices), each of which acts as the single isocline of a right rotation and the single isocline of a left rotation in two different fibrations.

Below, a spinning 5-cell is visualized with the fourth dimension squashed and displayed as colour. The Clifford torus is depicted in its rectangular (wrapping) form.

• Visualization of 4D rotations
• Simply rotating in X-Y plane
• Simply rotating in Z-W plane
• Double rotating in X-Y and Z-W planes with angular velocities in a 4:3 ratio
• Left isoclinic rotation
• Right isoclinic rotation

Projections

The A₄ Coxeter plane projects the 5-cell into a regular pentagon and pentagram. The A₃ Coxeter plane projection of the 5-cell is that of a square pyramid. The A₂ Coxeter plane projection of the regular 5-cell is that of a triangular bipyramid (two tetrahedra joined face-to-face) with the two opposite vertices centered.

orthographic projections

Ak Coxeter plane	A4	A3	A2
Graph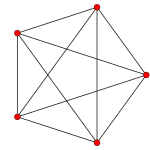
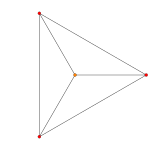
Dihedral symmetry

Projections to 3 dimensions
The vertex-first projection of the 5-cell into 3 dimensions has a tetrahedral projection envelope. The closest vertex of the 5-cell projects to the center of the tetrahedron, as shown here in red. The farthest cell projects onto the tetrahedral envelope itself, while the other 4 cells project onto the 4 flattened tetrahedral regions surrounding the central vertex.	The edge-first projection of the 5-cell into 3 dimensions has a triangular dipyramidal envelope. The closest edge (shown here in red) projects to the axis of the dipyramid, with the three cells surrounding it projecting to 3 tetrahedral volumes arranged around this axis at 120 degrees to each other. The remaining 2 cells project to the two halves of the dipyramid and are on the far side of the pentatope.
The face-first projection of the 5-cell into 3 dimensions also has a triangular dipyramidal envelope. The nearest face is shown here in red. The two cells that meet at this face project to the two halves of the dipyramid. The remaining three cells are on the far side of the pentatope from the 4D viewpoint, and are culled from the image for clarity. They are arranged around the central axis of the dipyramid, just as in the edge-first projection.	The cell-first projection of the 5-cell into 3 dimensions has a tetrahedral envelope. The nearest cell projects onto the entire envelope, and, from the 4D viewpoint, obscures the other 4 cells; hence, they are not rendered here.

Irregular 5-cells

In the case of simplexes such as the 5-cell, certain irregular forms are in some sense more fundamental than the regular form. Although regular 5-cells cannot fill 4-space or the regular 4-polytopes, there are irregular 5-cells which do. These characteristic 5-cells are the fundamental domains of the different symmetry groups which give rise to the various 4-polytopes.

Orthoschemes

A 4-orthoscheme is a 5-cell where all 10 faces are right triangles. (The 5 vertices form 5 tetrahedral cells face-bonded to each other, with a total of 10 edges and 10 triangular faces.) An orthoscheme is an irregular simplex that is the convex hull of a tree in which all edges are mutually perpendicular. In a 4-dimensional orthoscheme, the tree consists of four perpendicular edges connecting all five vertices in a linear path that makes three right-angled turns. The elements of an orthoscheme are also orthoschemes (just as the elements of a regular simplex are also regular simplexes). Each tetrahedral cell of a 4-orthoscheme is a 3-orthoscheme, and each triangular face is a 2-orthoscheme (a right triangle).

Orthoschemes are the characteristic simplexes of the regular polytopes, because each regular polytope is generated by reflections in the bounding facets of its particular characteristic orthoscheme. For example, the special case of the 4-orthoscheme with equal-length perpendicular edges is the characteristic orthoscheme of the 4-cube (also called the tesseract or 8-cell), the 4-dimensional analogue of the 3-dimensional cube. If the three perpendicular edges of the 4-orthoscheme are of unit length, then all its edges are of length √1, √2, √3, or √4, precisely the chord lengths of the unit 4-cube (the lengths of the 4-cube's edges and its various diagonals). Therefore this 4-orthoscheme fits within the 4-cube, and the 4-cube (like every regular convex polytope) can be dissected into instances of its characteristic orthoscheme.

A 3-orthoscheme is easily illustrated, but a 4-orthoscheme is more difficult to visualize. A 4-orthoscheme is a tetrahedral pyramid with a 3-orthoscheme as its base. It has four more edges than the 3-orthoscheme, joining the four vertices of the base to its apex (the fifth vertex of the 5-cell). Pick out any one of the 3-orthoschemes of the six shown in the 3-cube illustration. Notice that it touches four of the cube's eight vertices, and those four vertices are linked by a 3-edge path that makes two right-angled turns. Imagine that this 3-orthoscheme is the base of a 4-orthoscheme, so that from each of those four vertices, an unseen 4-orthoscheme edge connects to a fifth apex vertex (which is outside the 3-cube and does not appear in the illustration at all). Although the four additional edges all reach the same apex vertex, they will all be of different lengths. The first of them, at one end of the 3-edge orthogonal path, extends that path with a fourth orthogonal √1 edge by making a third 90 degree turn and reaching perpendicularly into the fourth dimension to the apex. The second of the four additional edges is a √2 diagonal of a cube face (not of the illustrated 3-cube, but of another of the tesseract's eight 3-cubes). The third additional edge is a √3 diagonal of a 3-cube (again, not the original illustrated 3-cube). The fourth additional edge (at the other end of the orthogonal path) is a long diameter of the tesseract itself, of length √4. It reaches through the exact center of the tesseract to the antipodal vertex (a vertex of the opposing 3-cube), which is the apex. Thus the characteristic 5-cell of the 4-cube has four √1 edges, three √2 edges, two √3 edges, and one √4 edge.

The 4-cube can be dissected into 24 such 4-orthoschemes eight different ways, with six 4-orthoschemes surrounding each of four orthogonal √4 tesseract long diameters. The 4-cube can also be dissected into 384 smaller instances of this same characteristic 4-orthoscheme, just one way, by all of its symmetry hyperplanes at once, which divide it into 384 4-orthoschemes that all meet at the center of the 4-cube.

More generally, any regular polytope can be dissected into g instances of its characteristic orthoscheme that all meet at the regular polytope's center. The number g is the order of the polytope, the number of reflected instances of its characteristic orthoscheme that comprise the polytope when a single mirror-surfaced orthoscheme instance is reflected in its own facets. More generally still, characteristic simplexes are able to fill uniform polytopes because they possess all the requisite elements of the polytope. They also possess all the requisite angles between elements (from 90 degrees on down). The characteristic simplexes are the genetic codes of polytopes: like a Swiss Army knife, they contain one of everything needed to construct the polytope by replication.

Every regular polytope, including the regular 5-cell, has its characteristic orthoscheme. There is a 4-orthoscheme which is the characteristic 5-cell of the regular 5-cell. It is a tetrahedral pyramid based on the characteristic tetrahedron of the regular tetrahedron. The regular 5-cell can be dissected into 120 instances of this characteristic 4-orthoscheme just one way, by all of its symmetry hyperplanes at once, which divide it into 120 4-orthoschemes that all meet at the center of the regular 5-cell.

Characteristics of the regular 5-cell
	edge	arc		dihedral
𝒍	${\displaystyle {\sqrt {\tfrac {5}{2}}}\approx 1.581}$	104°30′40″	${\displaystyle \pi -2{\text{𝜂}}}$	75°29′20″	${\displaystyle \pi -2{\text{𝟁}}}$
𝟀	${\displaystyle {\sqrt {\tfrac {1}{10}}}\approx 0.316}$	75°29′20″	${\displaystyle 2{\text{𝜂}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
𝝉	${\displaystyle {\sqrt {\tfrac {1}{30}}}\approx 0.183}$	52°15′20″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜂}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
𝟁	${\displaystyle {\sqrt {\tfrac {2}{15}}}\approx 0.103}$	52°15′20″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜂}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
${\displaystyle _{0}R^{3}/l}$	${\displaystyle {\sqrt {\tfrac {3}{20}}}\approx 0.387}$	75°29′20″	${\displaystyle 2{\text{𝜂}}}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
${\displaystyle _{1}R^{3}/l}$	${\displaystyle {\sqrt {\tfrac {1}{20}}}\approx 0.224}$	52°15′20″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜂}}}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
${\displaystyle _{2}R^{3}/l}$	${\displaystyle {\sqrt {\tfrac {1}{60}}}\approx 0.129}$	52°15′20″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜂}}}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
${\displaystyle _{0}R^{4}/l}$	${\displaystyle {\sqrt {1}}=1.0}$
${\displaystyle _{1}R^{4}/l}$	${\displaystyle {\sqrt {\tfrac {3}{8}}}\approx 0.612}$
${\displaystyle _{2}R^{4}/l}$	${\displaystyle {\sqrt {\tfrac {1}{6}}}\approx 0.408}$
${\displaystyle _{3}R^{4}/l}$	${\displaystyle {\sqrt {\tfrac {1}{16}}}=0.25}$
${\displaystyle {\text{𝜼}}}$		37°44′40″	${\displaystyle {\tfrac {{\text{arc sec }}4}{2}}}$

The characteristic 5-cell (4-orthoscheme) of the regular 5-cell has four more edges than its base characteristic tetrahedron (3-orthoscheme), which join the four vertices of the base to its apex (the fifth vertex of the 4-orthoscheme, at the center of the regular 5-cell). The four edges of each 4-orthoscheme which meet at the center of a regular 4-polytope are of unequal length, because they are the four characteristic radii of the regular 4-polytope: a vertex radius, an edge center radius, a face center radius, and a cell center radius. If the regular 5-cell has unit radius and edge length ${\displaystyle {\sqrt {\tfrac {5}{2}}}}$, its characteristic 5-cell's ten edges have lengths ${\displaystyle {\sqrt {\tfrac {1}{10}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{30}}}}$, ${\displaystyle {\sqrt {\tfrac {2}{15}}}}$ around its exterior right-triangle face (the edges opposite the characteristic angles 𝟀, 𝝉, 𝟁), plus ${\displaystyle {\sqrt {\tfrac {3}{20}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{20}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{60}}}}$ (the other three edges of the exterior 3-orthoscheme facet the characteristic tetrahedron, which are the characteristic radii of the regular tetrahedron), plus ${\displaystyle {\sqrt {1}}}$, ${\displaystyle {\sqrt {\tfrac {3}{8}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{6}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{16}}}}$ (edges which are the characteristic radii of the regular 5-cell). The 4-edge path along orthogonal edges of the orthoscheme is ${\displaystyle {\sqrt {\tfrac {1}{30}}}}$, ${\displaystyle {\sqrt {\tfrac {2}{15}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{60}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{16}}}}$, first from a regular 5-cell vertex to a regular 5-cell edge center, then turning 90° to a regular 5-cell face center, then turning 90° to a regular 5-cell tetrahedral cell center, then turning 90° to the regular 5-cell center.

Isometries

There are many lower symmetry forms of the 5-cell, including these found as uniform polytope vertex figures:

Symmetry	Order 120	Order 24	Order 12	Order 6	~ Order 10
Name	Regular 5-cell	Tetrahedral pyramid		Triangular pyramidal pyramid
Schläfli	{3,3,3}	{3,3}∨( )	{3}∨{ }	{3}∨( )∨( )
Example Vertex figure	5-simplex	Truncated 5-simplex	Bitruncated 5-simplex	Cantitruncated 5-simplex	Omnitruncated 4-simplex honeycomb

The tetrahedral pyramid is a special case of a 5-cell, a polyhedral pyramid, constructed as a regular tetrahedron base in a 3-space hyperplane, and an apex point above the hyperplane. The four sides of the pyramid are made of triangular pyramid cells.

Many uniform 5-polytopes have tetrahedral pyramid vertex figures with Schläfli symbols ( )∨{3,3}.

Symmetry , order 24

Schlegel diagram
Name Coxeter	{ }×{3,3,3}	{ }×{4,3,3}	{ }×{5,3,3}	t{3,3,3,3}	t{4,3,3,3}	t{3,4,3,3}

Other uniform 5-polytopes have irregular 5-cell vertex figures. The symmetry of a vertex figure of a uniform polytope is represented by removing the ringed nodes of the Coxeter diagram.

Symmetry	, order 12		, order 6		, order 8	, order 4
Schläfli	{3}∨{  }		{3}∨( )∨( )		{ }∨{ }∨( )
Schlegel diagram
Name Coxeter	t12α5	t12γ5	t012α5	t012γ5	t123α5	t123γ5

Symmetry	, order 2			, order 2	, order 1
Schläfli	{ }∨( )∨( )∨( )			( )∨( )∨( )∨( )∨( )
Schlegel diagram
Name Coxeter	t0123α5	t0123γ5	t0123β5	t01234α5	t01234γ5

Construction

As a Boerdijk–Coxeter helix

A 5-cell can be constructed as a Boerdijk–Coxeter helix of five chained tetrahedra, folded into a 4-dimensional ring. The 10 triangle faces can be seen in a 2D net within a triangular tiling, with 6 triangles around every vertex, although folding into 4-dimensions causes edges to coincide. The purple edges form a regular pentagon which is the Petrie polygon of the 5-cell. The blue edges connect every second vertex, forming a pentagram which is the Clifford polygon of the 5-cell. The pentagram's blue edges are the chords of the 5-cell's isocline, the circular rotational path its vertices take during an isoclinic rotation, also known as a Clifford displacement.

Net

When a net of five tetrahedra is folded up in 4-dimensional space such that each tetrahedron is face bonded to the other four, the resulting 5-cell has a total of 5 vertices, 10 edges, and 10 faces. Four edges meet at each vertex, and three tetrahedral cells meet at each edge. This makes the six tetrahedron as its cell.

Coordinates

The simplest set of Cartesian coordinates is: (2,0,0,0), (0,2,0,0), (0,0,2,0), (0,0,0,2), (𝜙,𝜙,𝜙,𝜙), with edge length 2√2, where 𝜙 is the golden ratio. While these coordinates are not origin-centered, subtracting ${\displaystyle (1,1,1,1)/(2-{\tfrac {1}{\phi }})}$ from each translates the 4-polytope's circumcenter to the origin with radius ${\displaystyle 2(\phi -1/(2-{\tfrac {1}{\phi }}))={\sqrt {\tfrac {16}{5}}}\approx 1.7888}$, with the following coordinates:

${\displaystyle \left({\tfrac {2}{\phi }}-3,1,1,1\right)/({\tfrac {1}{\phi }}-2)}$

${\displaystyle \left(1,{\tfrac {2}{\phi }}-3,1,1\right)/({\tfrac {1}{\phi }}-2)}$

${\displaystyle \left(1,1,{\tfrac {2}{\phi }}-3,1\right)/({\tfrac {1}{\phi }}-2)}$

${\displaystyle \left(1,1,1,{\tfrac {2}{\phi }}-3\right)/({\tfrac {1}{\phi }}-2)}$

${\displaystyle \left({\tfrac {2}{\phi }},{\tfrac {2}{\phi }},{\tfrac {2}{\phi }},{\tfrac {2}{\phi }}\right)/({\tfrac {1}{\phi }}-2)}$

The following set of origin-centered coordinates with the same radius and edge length as above can be seen as a hyperpyramid with a regular tetrahedral base in 3-space:

${\displaystyle \left(1,1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(1,-1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,-1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(0,0,0,{\frac {4}{\sqrt {5}}}\right)}$

Scaling these or the previous set of coordinates by ${\displaystyle {\tfrac {\sqrt {5}}{4}}}$ give unit-radius origin-centered regular 5-cells with edge lengths ${\displaystyle {\sqrt {\tfrac {5}{2}}}}$. The hyperpyramid has coordinates:

${\displaystyle \left({\sqrt {5}},{\sqrt {5}},{\sqrt {5}},-1\right)/4}$

${\displaystyle \left({\sqrt {5}},-{\sqrt {5}},-{\sqrt {5}},-1\right)/4}$

${\displaystyle \left(-{\sqrt {5}},{\sqrt {5}},-{\sqrt {5}},-1\right)/4}$

${\displaystyle \left(-{\sqrt {5}},-{\sqrt {5}},{\sqrt {5}},-1\right)/4}$

${\displaystyle \left(0,0,0,1\right)}$

Coordinates for the vertices of another origin-centered regular 5-cell with edge length 2 and radius ${\displaystyle {\sqrt {\tfrac {8}{5}}}\approx 1.265}$ are:

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ 0\right)}$

${\displaystyle \left(-2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)}$

Scaling these by ${\displaystyle {\sqrt {\tfrac {5}{8}}}}$ to unit-radius and edge length ${\displaystyle {\sqrt {\tfrac {5}{2}}}}$ gives:

${\displaystyle \left({\sqrt {3}},{\sqrt {5}},{\sqrt {10}},\pm {\sqrt {30}}\right)/(4{\sqrt {3}})}$

${\displaystyle \left({\sqrt {3}},{\sqrt {5}},-{\sqrt {40}},0\right)/(4{\sqrt {3}})}$

${\displaystyle \left({\sqrt {3}},-{\sqrt {45}},0,0\right)/(4{\sqrt {3}})}$

${\displaystyle \left(-1,0,0,0\right)}$

The vertices of a 4-simplex (with edge √2 and radius 1) can be more simply constructed on a hyperplane in 5-space, as (distinct) permutations of (0,0,0,0,1) or (0,1,1,1,1); in these positions it is a facet of, respectively, the 5-orthoplex or the rectified penteract.

Compound

The compound of two 5-cells in dual configurations can be seen in this A5 Coxeter plane projection, with a red and blue 5-cell vertices and edges. This compound has ] symmetry, order 240. The intersection of these two 5-cells is a uniform bitruncated 5-cell. = ∩ .

This compound can be seen as the 4D analogue of the 2D hexagram {⁠6/2⁠} and the 3D compound of two tetrahedra.

Related polytopes and honeycombs

The pentachoron (5-cell) is the simplest of 9 uniform polychora constructed from the Coxeter group.

Schläfli	{3,3,3}	t{3,3,3}	r{3,3,3}	rr{3,3,3}	2t{3,3,3}	tr{3,3,3}	t0,3{3,3,3}	t0,1,3{3,3,3}	t0,1,2,3{3,3,3}
Coxeter
Schlegel

1k2 figures in n dimensions
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\displaystyle {\tilde {E}}_{8}}$ = E8	E10 = ${\displaystyle {\bar {T}}_{8}}$ = E8
Coxeter diagram
Symmetry (order)				]
Order	12	120	1,920	103,680	2,903,040	696,729,600	∞
Graph							-	-
Name	1−1,2	102	112	122	132	142	152	162

2k1 figures in n dimensions
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\displaystyle {\tilde {E}}_{8}}$ = E8	E10 = ${\displaystyle {\bar {T}}_{8}}$ = E8
Coxeter diagram
Symmetry			]
Order	12	120	384	51,840	2,903,040	696,729,600	∞
Graph							-	-
Name	2−1,1	201	211	221	231	241	251	261

It is in the {p,3,3} sequence of regular polychora with a tetrahedral vertex figure: the tesseract {4,3,3} and 120-cell {5,3,3} of Euclidean 4-space, and the hexagonal tiling honeycomb {6,3,3} of hyperbolic space.

{p,3,3} polytopes
Space		S			H
Form		Finite			Paracompact	Noncompact
Name		{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	...{∞,3,3}
Image
Cells {p,3}		{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

It is one of three {3,3,p} regular 4-polytopes with tetrahedral cells, along with the 16-cell {3,3,4} and 600-cell {3,3,5}. The order-6 tetrahedral honeycomb {3,3,6} of hyperbolic space also has tetrahedral cells.

{3,3,p} polytopes
Space	S			H
Form	Finite			Paracompact	Noncompact
Name	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	... {3,3,∞}
Image
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

It is self-dual like the 24-cell {3,4,3}, having a palindromic {3,p,3} Schläfli symbol.

{3,p,3} polytopes
Space	S		H
Form	Finite		Compact	Paracompact	Noncompact
{3,p,3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Image
Cells	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}
Vertex figure	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

{p,3,p} regular honeycombs
Space	S	Euclidean E	H
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Notes

1. ^ (Coxeter 1973) uses the greek letter 𝝓 (phi) to represent one of the three characteristic angles 𝟀, 𝝓, 𝟁 of a regular polytope. Because 𝝓 is commonly used to represent the golden ratio constant ≈ 1.618, for which Coxeter uses 𝝉 (tau), we reverse Coxeter's conventions, and use 𝝉 to represent the characteristic angle.

Citations

1. Johnson 2018, p. 249.
2. Ghyka 1977, p. 68.
3. Coxeter 1973, p. 120, §7.2. see illustration Fig 7.2A.
4. Miyazaki & Ishii 2021, p. 46.
5. Diudea 2018, p. 41.
6. ^ Akiyama, Hitotumatu & Sato 2012.
7. Coxeter 1973, pp. 292–293, Table I(ii): The sixteen regular polytopes {p,q,r} in four dimensions.
8. Coxeter 1973, p. 12, §1.8. Configurations.
9. "Pen".
10. Coxeter 1973, pp. 198–202, §11.7 Regular figures and their truncations.
11. Kim & Rote 2016, pp. 17–20, §10 The Coxeter Classification of Four-Dimensional Point Groups.
12. Coxeter 1973, pp. 292–293, Table I(ii); "5-cell, 𝛼₄".
13. Coxeter 1973, p. 139, §7.9 The characteristic simplex.
14. Coxeter 1973, p. 290, Table I(ii); "dihedral angles".
15. Banchoff 2013.
16. Coxeter 1991, p. 30, §4.2. The Crystallographic regular polytopes.

References

• Akiyama, Jin; Hitotumatu, Sin; Sato, Ikuro (2012). "Determination of the element numbers of the regular polytopes". Geometriae Dedicata. 159: 89–97. doi:10.1007/s10711-011-9647-3.
• Diudea, M. V. (2018). Multi-shell Polyhedral Clusters. Carbon Materials: Chemistry and Physics. Vol. 10. Springer. doi:10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
• Ghyka, Matila (1977). The Geometry of Art and Life. Dover Publications. ISBN 978-0-486-23542-4.
• Johnson, N. W. (2018). "Finite Symmetry Groups, 11.5 Spherical Coxeter groups". Geometries and Transformations. Cambridge University Press. ISBN 978-1-107-10340-5.
• Miyazaki, K.; Ishii, M. (2021). "Symmetry in Projection of 4-Dimensional Regular Polychora". In Darvas, György (ed.). Complex Symmetries. doi:10.1007/978-3-030-88059-0. ISBN 978-3-030-88059-0.
• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• H.S.M. Coxeter:
  • Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
    • p. 120, §7.2. see illustration Fig 7.2A
    • p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Coxeter, H.S.M. (1991), Regular Complex Polytopes (2nd ed.), Cambridge: Cambridge University Press
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I,
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II,
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
• Kim, Heuna; Rote, G. (2016). "Congruence Testing of Point Sets in 4 Dimensions". arXiv:1603.07269 .
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
• Banchoff, Thomas F. (2013). "Torus Decompostions of Regular Polytopes in 4-space". In Senechal, Marjorie (ed.). Shaping Space. Springer New York. pp. 257–266. doi:10.1007/978-0-387-92714-5_20. ISBN 978-0-387-92713-8.

External links

• Weisstein, Eric W. "Pentatope". MathWorld.
• Klitzing, Richard. "4D uniform polytopes (polychora) x3o3o3o - pen".
• Der 5-Zeller (5-cell) Marco Möller's Regular polytopes in R (German)
• Jonathan Bowers, Regular polychora
• Java3D Applets
• pyrochoron

• Regular 4-polytopes
• Pyramids (geometry)