Misplaced Pages

Prism graph

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Graph with a prism as its skeleton

In the mathematical field of graph theory, a prism graph is a graph that has one of the prisms as its skeleton.

Examples

The individual graphs may be named after the associated solid:


Y3 = GP(3,1)
Y4 = Q3 = GP(4,1)
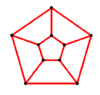Y5 = GP(5,1)
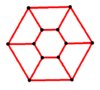Y6 = GP(6,1)
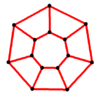Y7 = GP(7,1)
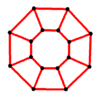Y8 = GP(8,1)

Although geometrically the star polygons also form the faces of a different sequence of (self-intersecting and non-convex) prismatic polyhedra, the graphs of these star prisms are isomorphic to the prism graphs, and do not form a separate sequence of graphs.

Construction

Prism graphs are examples of generalized Petersen graphs, with parameters GP(n,1). They may also be constructed as the Cartesian product of a cycle graph with a single edge.

As with many vertex-transitive graphs, the prism graphs may also be constructed as Cayley graphs. The order-n dihedral group is the group of symmetries of a regular n-gon in the plane; it acts on the n-gon by rotations and reflections. It can be generated by two elements, a rotation by an angle of 2π/n and a single reflection, and its Cayley graph with this generating set is the prism graph. Abstractly, the group has the presentation ⟨ r , f ∣ r n , f 2 , ( r f ) 2 ⟩ {\displaystyle \langle r,f\mid r^{n},f^{2},(rf)^{2}\rangle } (where r is a rotation and f is a reflection or flip) and the Cayley graph has r and f (or r, r, and f) as its generators.

The n-gonal prism graphs with odd values of n may be constructed as circulant graphs C 2 n 2 , n {\displaystyle C_{2n}^{2,n}} . However, this construction does not work for even values of n.

Properties

The graph of an n-gonal prism has 2n vertices and 3n edges. They are regular, cubic graphs. Since the prism has symmetries taking each vertex to each other vertex, the prism graphs are vertex-transitive graphs. As polyhedral graphs, they are also 3-vertex-connected planar graphs. Every prism graph has a Hamiltonian cycle.

Among all biconnected cubic graphs, the prism graphs have within a constant factor of the largest possible number of 1-factorizations. A 1-factorization is a partition of the edge set of the graph into three perfect matchings, or equivalently an edge coloring of the graph with three colors. Every biconnected n-vertex cubic graph has O(2) 1-factorizations, and the prism graphs have Ω(2) 1-factorizations.

The number of spanning trees of an n-gonal prism graph is given by the formula

n 2 ( ( 2 + 3 ) n + ( 2 − 3 ) n − 2 ) {\displaystyle {\frac {n}{2}}{\bigl (}(2+{\sqrt {3}})^{n}+(2-{\sqrt {3}})^{n}-2){\bigr .}}

For n = 3, 4, 5, ... these numbers are

75, 384, 1805, 8100, 35287, 150528, ... (sequence A006235 in the OEIS).

The n-gonal prism graphs for even values of n are partial cubes. They form one of the few known infinite families of cubic partial cubes, and (except for four sporadic examples) the only vertex-transitive cubic partial cubes.

The pentagonal prism is one of the forbidden minors for the graphs of treewidth three. The triangular prism and cube graph have treewidth exactly three, but all larger prism graphs have treewidth four.

Related graphs

Other infinite sequences of polyhedral graph formed in a similar way from polyhedra with regular-polygon bases include the antiprism graphs (graphs of antiprisms) and wheel graphs (graphs of pyramids). Other vertex-transitive polyhedral graphs include the Archimedean graphs.

If the two cycles of a prism graph are broken by the removal of a single edge in the same position in both cycles, the result is a ladder graph. If these two removed edges are replaced by two crossed edges, the result is a non-planar graph called a Möbius ladder.

References

  1. ^ Weisstein, Eric W. "Prism graph". MathWorld.
  2. Read, R. C. and Wilson, R. J. An Atlas of Graphs, Oxford, England: Oxford University Press, 2004 reprint, Chapter 6 special graphs pp. 261, 270.
  3. Eppstein, David (2013), "The complexity of bendless three-dimensional orthogonal graph drawing", Journal of Graph Algorithms and Applications, 17 (1): 35–55, arXiv:0709.4087, doi:10.7155/jgaa.00283, MR 3019198, S2CID 2716392. Eppstein credits the observation that prism graphs have close to the maximum number of 1-factorizations to a personal communication by Greg Kuperberg.
  4. Jagers, A. A. (1988), "A note on the number of spanning trees in a prism graph", International Journal of Computer Mathematics, 24 (2): 151–154, doi:10.1080/00207168808803639.
  5. Marc, Tilen (2015), Classification of vertex-transitive cubic partial cubes, arXiv:1509.04565, Bibcode:2015arXiv150904565M.
  6. Arnborg, Stefan; Proskurowski, Andrzej; Corneil, Derek G. (1990), "Forbidden minors characterization of partial 3-trees", Discrete Mathematics, 80 (1): 1–19, doi:10.1016/0012-365X(90)90292-P, MR 1045920.
  7. Guy, Richard K.; Harary, Frank (1967), "On the Möbius ladders", Canadian Mathematical Bulletin, 10 (4): 493–496, doi:10.4153/CMB-1967-046-4, MR 0224499.
Categories: