Misplaced Pages

Section modulus

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Geometric property of a structural member

In solid mechanics and structural engineering, section modulus is a geometric property of a given cross-section used in the design of beams or flexural members. Other geometric properties used in design include: area for tension and shear, radius of gyration for compression, and second moment of area and polar second moment of area for stiffness. Any relationship between these properties is highly dependent on the shape in question. There are two types of section modulus, elastic and plastic:

  • The elastic section modulus is used to calculate a cross-section's resistance to bending within the elastic range, where stress and strain are proportional.
  • The plastic section modulus is used to calculate a cross-section's capacity to resist bending after yielding has occurred across the entire section. It is used for determining the plastic, or full moment, strength and is larger than the elastic section modulus, reflecting the section's strength beyond the elastic range.

Equations for the section moduli of common shapes are given below. The section moduli for various profiles are often available as numerical values in tables that list the properties of standard structural shapes.

Note: Both the elastic and plastic section moduli are different to the first moment of area. It is used to determine how shear forces are distributed.

Notation

Different codes use varying notations for the elastic and plastic section modulus, as illustrated in the table below.

Section Modulus Notation
Region Code Section Modulus
Elastic Plastic
North America USA: ANSI/AISC 360-10 S Z
Canada: CSA S16-14 S Z
Europe Europe (inc. Britain): Eurocode 3 Wel Wpl
Britain (obsolete): BS 5950 Z S
Asia Japan: Standard Specifications for Steel and Composite Structures W Z
China: GB 50017 W Wp
India: IS 800 Ze Zp
Australia: AS 4100 Z S
Notes:

a) Withdrawn on 30 March 2010, Eurocode 3 is used instead.

The North American notation is used in this article.

Elastic section modulus

The elastic section modulus is used for general design. It is applicable up to the yield point for most metals and other common materials. It is defined as

S = I c {\displaystyle S={\frac {I}{c}}}

where:

I is the second moment of area (or area moment of inertia, not to be confused with moment of inertia), and
c is the distance from the neutral axis to the most extreme fibre.

It is used to determine the yield moment strength of a section

M y = S ⋅ σ y {\displaystyle M_{y}=S\cdot \sigma _{y}}

where σy is the yield strength of the material.

The table below shows formulas for the elastic section modulus for various shapes.

Elastic Section Modulus Equations
Cross-sectional shape Figure Equation Comment Ref.
Rectangle S = b h 2 6 {\displaystyle S={\cfrac {bh^{2}}{6}}} Solid arrow represents neutral axis
doubly symmetric Ɪ-section (major axis) S x = B H 2 6 − b h 3 6 H {\displaystyle S_{x}={\cfrac {BH^{2}}{6}}-{\cfrac {bh^{3}}{6H}}}

S x = I x y {\displaystyle S_{x}={\tfrac {I_{x}}{y}}} ,

with y = H 2 {\displaystyle y={\cfrac {H}{2}}}

NA indicates neutral axis
doubly symmetric Ɪ-section (minor axis) S y = B 2 ( H − h ) 6 + ( B − b ) 3 h 6 B {\displaystyle S_{y}={\cfrac {B^{2}(H-h)}{6}}+{\cfrac {(B-b)^{3}h}{6B}}} NA indicates neutral axis
Circle S = π d 3 32 {\displaystyle S={\cfrac {\pi d^{3}}{32}}} Solid arrow represents neutral axis
Circular hollow section 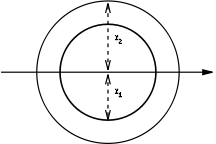S = π ( r 2 4 − r 1 4 ) 4 r 2 = π ( d 2 4 − d 1 4 ) 32 d 2 {\displaystyle S={\cfrac {\pi \left(r_{2}^{4}-r_{1}^{4}\right)}{4r_{2}}}={\cfrac {\pi (d_{2}^{4}-d_{1}^{4})}{32d_{2}}}} Solid arrow represents neutral axis
Rectangular hollow section 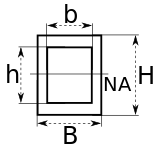S = B H 2 6 − b h 3 6 H {\displaystyle S={\cfrac {BH^{2}}{6}}-{\cfrac {bh^{3}}{6H}}} NA indicates neutral axis
Diamond S = B H 2 24 {\displaystyle S={\cfrac {BH^{2}}{24}}} NA indicates neutral axis
C-channel 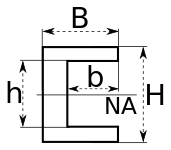S = B H 2 6 − b h 3 6 H {\displaystyle S={\cfrac {BH^{2}}{6}}-{\cfrac {bh^{3}}{6H}}} NA indicates neutral axis
Equal and Unequal

Angles

These sections require careful consideration because the axes for the maximum and minimum

section modulus are not parallel with its flanges. Tables of values for standard sections are available.

Plastic section modulus

The plastic section modulus is used for materials and structures where limited plastic deformation is acceptable. It represents the section's capacity to resist bending once the material has yielded and entered the plastic range. It is used to determine the plastic, or full, moment strength of a section

M p = Z ⋅ σ y {\displaystyle M_{p}=Z\cdot \sigma _{y}}

where σy is the yield strength of the material.

Engineers often compare the plastic moment strength against factored applied moments to ensure that the structure can safely endure the required loads without significant or unacceptable permanent deformation. This is an integral part of the limit state design method.

The plastic section modulus depends on the location of the plastic neutral axis (PNA). The PNA is defined as the axis that splits the cross section such that the compression force from the area in compression equals the tension force from the area in tension. For sections with constant, equal compressive and tensile yield strength, the area above and below the PNA will be equal

A C = A T {\displaystyle A_{C}=A_{T}}

These areas may differ in composite sections, which have differing material properties, resulting in unequal contributions to the plastic section modulus.

The plastic section modulus is calculated as the sum of the areas of the cross section on either side of the PNA, each multiplied by the distance from their respective local centroids to the PNA.

Z = A C y C + A T y T {\displaystyle Z=A_{C}y_{C}+A_{T}y_{T}}

where:

AC is the area in compression
AT is the area in tension
yC, yT are the distances from the PNA to their centroids.

Plastic section modulus and elastic section modulus can be related by a shape factor k:

k = M p M y = Z S {\displaystyle k={\frac {M_{p}}{M_{y}}}={\frac {Z}{S}}}

This is an indication of a section's capacity beyond the yield strength of material. The shape factor for a rectangular section is 1.5.

The table below shows formulas for the plastic section modulus for various shapes.

Plastic Section Modulus Equations
Description Figure Equation Comment Ref.
Rectangular section Z = b h 2 4 {\displaystyle Z={\frac {bh^{2}}{4}}}
A C = A T = b h 2 {\displaystyle A_{C}=A_{T}={\frac {bh}{2}}} y C = y T = h 4 {\displaystyle y_{C}=y_{T}={\frac {h}{4}}}

Rectangular hollow section Z = b h 2 4 − ( b − 2 t ) ( h 2 − t ) 2 {\displaystyle Z={\cfrac {bh^{2}}{4}}-(b-2t)\left({\cfrac {h}{2}}-t\right)^{2}} b = width,
h = height,
t = wall thickness
For the two flanges of an Ɪ-beam with the web excluded Z = b 1 t 1 y 1 + b 2 t 2 y 2 {\displaystyle Z=b_{1}t_{1}y_{1}+b_{2}t_{2}y_{2}\,} b1, b2 = width,
t1, t2 = thickness,
y1, y2 = distances from the neutral axis to the centroids of the flanges respectively.
For an I Beam including the web Z = b t f ( d − t f ) + t w ( d − 2 t f ) 2 4 {\displaystyle Z=bt_{f}(d-t_{f})+{\frac {t_{w}(d-2t_{f})^{2}}{4}}}

For an I Beam (weak axis) Z = b 2 t f 2 + t w 2 ( d − 2 t f ) 4 {\displaystyle Z={\frac {b^{2}t_{f}}{2}}+{\frac {t_{w}^{2}(d-2t_{f})}{4}}} d = full height of the I beam
Solid Circle Z = d 3 6 {\displaystyle Z={\cfrac {d^{3}}{6}}}
Circular hollow section Z = d 2 3 − d 1 3 6 {\displaystyle Z={\cfrac {d_{2}^{3}-d_{1}^{3}}{6}}}
Equal and Unequal Angles These sections require careful consideration because the axes for the maximum and minimum

section modulus are not parallel with its flanges.

Use in structural engineering

In structural engineering, the choice between utilizing the elastic or plastic (full moment) strength of a section is determined by the specific application. Engineers follow relevant codes that dictate whether an elastic or plastic design approach is appropriate, which in turn informs the use of either the elastic or plastic section modulus. While a detailed examination of all relevant codes is beyond the scope of this article, the following observations are noteworthy:

  • When assessing the strength of long, slender beams, it is essential to evaluate their capacity to resist lateral torsional buckling in addition to determining their moment capacity based on the section modulus.
  • Although T-sections may not be the most efficient choice for resisting bending, they are sometimes selected for their architectural appeal. In such cases, it is crucial to carefully assess their capacity to resist lateral torsional buckling.
  • While standard uniform cross-section beams are often used, they may not be optimally utilized when subjected to load moments that vary along their length. For large beams with predictable loading conditions, strategically adjusting the section modulus along the length can significantly enhance efficiency and cost-effectiveness.
  • In certain applications, such as cranes and aeronautical or space structures, relying solely on calculations is often deemed insufficient. In these cases, structural testing is conducted to validate the load capacity of the structure.

See also

References

  1. ^ Young, Warren C. (1989). Roark's Formulas for Stress and Strain (PDF). McGraw Hill. p. 217.
  2. "'Blue Book' home - Blue Book - Steel for Life". www.steelforlifebluebook.co.uk. Retrieved 2024-08-25.
  3. "Specification for Structural Steel Buildings (ANSI/AISC 360-10) - 2010 | American Institute of Steel Construction". www.aisc.org. Retrieved 2024-08-23.
  4. S16-14 (R2019) Design of steel structures. Canadian Standards Association. 2024-08-23.
  5. Eurocode 3: Design of steel structures - Part 1-1: General rules and rules for buildings. ISBN 978 0 539 13167 3.
  6. BS 5950-1 Structural use of steelwork in building, BSI British Standards, retrieved 2024-08-23
  7. Standard Specifications for Steel and Composite Structures (First ed.). Japan: Japan Society of Civil Engineers (published December 2009). 2024-08-24.
  8. GB 50017 Code for Design of Steel Structures. China: Ministry of Construction of the People's Republic of China (published 2003-04-25). 2003.
  9. IS800:2007 General Construction in Steel - Code of Practice (Third ed.). India: Bureau of Indian Standards (published 2017). 2007.
  10. AS 4100- 2020 Steel Structures. Australia: Standards Australia Ltd. 2020. ISBN 978 1 76072 947 9.
  11. "British Standards Institute". 2024-08-23. Retrieved 2024-08-23.
  12. ^ Gere, J. M. and Timnko, S., 1997, Mechanics of Materials 4th Ed., PWS Publishing Co.
  13. "Section Modulus Equations and Calculators Common Shapes".
  14. ^ Trahair, N. S. (2002-11-01). "Moment Capacities of Steel Angle Sections". Journal of Structural Engineering. 128 (11): 1387–1393. doi:10.1061/(asce)0733-9445(2002)128:11(1387). ISSN 0733-9445.
  15. ^ "Section properties - Dimensions & properties - Blue Book - Steel for Life". www.steelforlifebluebook.co.uk. Retrieved 2024-08-27.
  16. ^ "Plastic Modulus" (PDF).
  17. "Calculating the section modulus".
  18. American Institute of Steel Construction: Load and Resistance Factor Design, 3rd Edition, pp. 17-34.
  19. Megson, T H G (2005). Structural and stress analysis. elsever. pp. 598 EQ (iv). ISBN 9780080455341.
  20. Brockenbrough, Roger L.; Merritt, Frederick S., eds. (1999). Structural steel designer's handbook. McGraw-Hill handbooks (3 ed.). New York: McGraw-Hill. p. 3.96. ISBN 978-0-07-008782-8.
  21. Brown, David (2024-08-27). "The design of tee sections in bending" (PDF). New Steel Construction.
  22. Vu, Huy Hoang; Chu, Thi Hoang Anh (2024). "Simply supported built-up I-beam optimization comparison". E3S Web of Conferences. 533: 02010. doi:10.1051/e3sconf/202453302010. ISSN 2267-1242.
Categories: