In the mathematical field of graph theory, an automorphism is a permutation of the vertices such that edges are mapped to edges and non-edges are mapped to non-edges. A graph is a vertex-transitive graph if, given any two vertices v1 and v2 of G, there is an automorphism f such that
In other words, a graph is vertex-transitive if its automorphism group acts transitively on its vertices. A graph is vertex-transitive if and only if its graph complement is, since the group actions are identical.
Every symmetric graph without isolated vertices is vertex-transitive, and every vertex-transitive graph is regular. However, not all vertex-transitive graphs are symmetric (for example, the edges of the truncated tetrahedron), and not all regular graphs are vertex-transitive (for example, the Frucht graph and Tietze's graph).
Finite examples
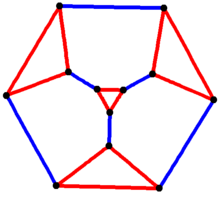
Finite vertex-transitive graphs include the symmetric graphs (such as the Petersen graph, the Heawood graph and the vertices and edges of the Platonic solids). The finite Cayley graphs (such as cube-connected cycles) are also vertex-transitive, as are the vertices and edges of the Archimedean solids (though only two of these are symmetric). Potočnik, Spiga and Verret have constructed a census of all connected cubic vertex-transitive graphs on at most 1280 vertices.
Although every Cayley graph is vertex-transitive, there exist other vertex-transitive graphs that are not Cayley graphs. The most famous example is the Petersen graph, but others can be constructed including the line graphs of edge-transitive non-bipartite graphs with odd vertex degrees.
Properties
The edge-connectivity of a connected vertex-transitive graph is equal to the degree d, while the vertex-connectivity will be at least 2(d + 1)/3. If the degree is 4 or less, or the graph is also edge-transitive, or the graph is a minimal Cayley graph, then the vertex-connectivity will also be equal to d.
Infinite examples
Infinite vertex-transitive graphs include:
- infinite paths (infinite in both directions)
- infinite regular trees, e.g. the Cayley graph of the free group
- graphs of uniform tessellations (see a complete list of planar tessellations), including all tilings by regular polygons
- infinite Cayley graphs
- the Rado graph
Two countable vertex-transitive graphs are called quasi-isometric if the ratio of their distance functions is bounded from below and from above. A well known conjecture stated that every infinite vertex-transitive graph is quasi-isometric to a Cayley graph. A counterexample was proposed by Diestel and Leader in 2001. In 2005, Eskin, Fisher, and Whyte confirmed the counterexample.
See also
References
- ^ Godsil, Chris; Royle, Gordon (2013) , Algebraic Graph Theory, Graduate Texts in Mathematics, vol. 207, Springer, ISBN 978-1-4613-0163-9.
- Potočnik P., Spiga P. & Verret G. (2013), "Cubic vertex-transitive graphs on up to 1280 vertices", Journal of Symbolic Computation, 50: 465–477, arXiv:1201.5317, doi:10.1016/j.jsc.2012.09.002, S2CID 26705221.
- Lauri, Josef; Scapellato, Raffaele (2003), Topics in graph automorphisms and reconstruction, London Mathematical Society Student Texts, vol. 54, Cambridge University Press, p. 44, ISBN 0-521-82151-7, MR 1971819. Lauri and Scapelleto credit this construction to Mark Watkins.
- Babai, L. (1996), Technical Report TR-94-10, University of Chicago, archived from the original on 2010-06-11
- Diestel, Reinhard; Leader, Imre (2001), "A conjecture concerning a limit of non-Cayley graphs" (PDF), Journal of Algebraic Combinatorics, 14 (1): 17–25, doi:10.1023/A:1011257718029, S2CID 10927964.
- Eskin, Alex; Fisher, David; Whyte, Kevin (2005). "Quasi-isometries and rigidity of solvable groups". arXiv:math.GR/0511647..
External links
- Weisstein, Eric W. "Vertex-transitive graph". MathWorld.
- A census of small connected cubic vertex-transitive graphs. Primož Potočnik, Pablo Spiga, Gabriel Verret, 2012.
- Vertex-transitive Graphs On Fewer Than 48 Vertices. Gordon Royle and Derek Holt, 2020.
