Misplaced Pages

Part of a series on
Renewable energy
Biofuel Biogas Biomass Carbon-neutral fuel Crosswind kite power Geothermal energy Geothermal heating Geothermal power Hydroelectricity Run-of-the-river Hydropower Micro hydro Pico hydro Small hydro Marine current power Marine energy Ocean thermal Osmotic power Solar energy Solar power Sustainable biofuel Tidal power Tidal stream generator Wave power Wind power
Nuclear power proposed as renewable energy
Topics by country and territory Marketing and policy trends
v t e

Part of a series on
Sustainable energy
Energy conservation Arcology Building insulation Cogeneration Compact fluorescent lamp Eco hotel Eco-cities Ecohouse Ecolabel Efficient energy use Energy audit Energy efficiency implementation Energy recovery Energy recycling Energy saving lamp Energy Star Energy storage Environmental planning Environmental technology Fossil fuel phase-out Glass in green buildings Green building and wood Green building Heat pump List of low-energy building techniques Low-energy house Microgeneration Passive house Passive solar building design Sustainable architecture Sustainable city Sustainable habitat Sustainable refurbishment Thermal energy storage Tropical green building Waste-to-energy Zero heating building Zero-energy building
Renewable energy Biofuel Sustainable Biogas Biomass Carbon-neutral fuel Geothermal energy Geothermal power Geothermal heating Hydropower Hydroelectricity Micro hydro Pico hydro Run-of-the-river Small hydro Marine current power Marine energy Tidal power Tidal barrage Tidal farm Tidal stream generator Ocean thermal energy conversion Renewable energy transition Renewable heat Solar Wave Wind Community Farm Floating wind turbine Forecasting Industry Lens Outline Rights Turbine Windbelt Windpump
Sustainable transport Green vehicle Electric vehicle Bicycle Solar vehicle Wind-powered vehicle Hybrid vehicle Human-electric Twike Plug-in Human-powered transport Helicopter Hydrofoil Land vehicle Bicycle Cycle rickshaw Kick scooter Quadracycle Tricycle Velomobile Roller skating Skateboarding Walking Watercraft Personal transporter Rail transport Tram Rapid transit Personal rapid transit
Category Renewable energy portal
v t e

Wave power is the capture of energy of wind waves to do useful work – for example, electricity generation, desalination, or pumping water. A machine that exploits wave power is a wave energy converter (WEC).

Waves are generated primarily by wind passing over the sea's surface and also by tidal forces, temperature variations, and other factors. As long as the waves propagate slower than the wind speed just above, energy is transferred from the wind to the waves. Air pressure differences between the windward and leeward sides of a wave crest and surface friction from the wind cause shear stress and wave growth.

Wave power as a descriptive term is different from tidal power, which seeks to primarily capture the energy of the current caused by the gravitational pull of the Sun and Moon. However, wave power and tidal power are not fundamentally distinct and have significant cross-over in technology and implementation. Other forces can create currents, including breaking waves, wind, the Coriolis effect, cabbeling, and temperature and salinity differences.

As of 2023, wave power is not widely employed for commercial applications, after a long series of trial projects. Attempts to use this energy began in 1890 or earlier, mainly due to its high power density. Just below the ocean's water surface the wave energy flow, in time-average, is typically five times denser than the wind energy flow 20 m above the sea surface, and 10 to 30 times denser than the solar energy flow.

In 2000 the world's first commercial wave power device, the Islay LIMPET was installed on the coast of Islay in Scotland and connected to the UK national grid. In 2008, the first experimental multi-generator wave farm was opened in Portugal at the Aguçadoura Wave Farm. Both projects have since ended. For a list of other wave power stations see List of wave power stations.

Wave energy converters can be classified based on their working principle as either:

• oscillating water columns (with air turbine)
• oscillating bodies (with hydroelectric motor, hydraulic turbine, linear electrical generator)
• overtopping devices (with low-head hydraulic turbine)

History

The first known patent to extract energy from ocean waves was in 1799, filed in Paris by Pierre-Simon Girard and his son. An early device was constructed around 1910 by Bochaux-Praceique to power his house in Royan, France. It appears that this was the first oscillating water-column type of wave-energy device. From 1855 to 1973 there were 340 patents filed in the UK alone.

Modern pursuit of wave energy was pioneered by Yoshio Masuda's 1940s experiments. He tested various concepts, constructing hundreds of units used to power navigation lights. Among these was the concept of extracting power from the angular motion at the joints of an articulated raft, which Masuda proposed in the 1950s.

The oil crisis in 1973 renewed interest in wave energy. Substantial wave-energy development programmes were launched by governments in several countries, in particular in the UK, Norway and Sweden. Researchers re-examined waves' potential to extract energy, notably Stephen Salter, Johannes Falnes, Kjell Budal, Michael E. McCormick, David Evans, Michael French, Nick Newman, and C. C. Mei.

Salter's 1974 invention became known as Salter's duck or nodding duck, officially the Edinburgh Duck. In small-scale tests, the Duck's curved cam-like body can stop 90% of wave motion and can convert 90% of that to electricity, giving 81% efficiency. In the 1980s, several other first-generation prototypes were tested, but as oil prices ebbed, wave-energy funding shrank. Climate change later reenergized the field.

The world's first wave energy test facility was established in Orkney, Scotland in 2003 to kick-start the development of a wave and tidal energy industry. The European Marine Energy Centre(EMEC) has supported the deployment of more wave and tidal energy devices than any other single site. Subsequent to its establishment test facilities occurred also in many other countries around the world, providing services and infrastructure for device testing.

The £10 million Saltire prize challenge was to be awarded to the first to be able to generate 100 GWh from wave power over a continuous two-year period by 2017 (about 5.7 MW average). The prize was never awarded. A 2017 study by Strathclyde University and Imperial College focused on the failure to develop "market ready" wave energy devices – despite a UK government investment of over £200 million over 15 years.

Public bodies have continued and in many countries stepped up the research and development funding for wave energy during the 2010s. This includes both EU, US and UK where the annual allocation has typically been in the range 5-50 million USD. Combined with private funding, this has led to a large number of ongoing wave energy projects (see List of wave power projects).

Physical concepts

Like most fluid motion, the interaction between ocean waves and energy converters is a high-order nonlinear phenomenon. It is described using the incompressible Navier-Stokes equations $${\displaystyle {\begin{aligned}{\frac {\partial {\vec {u}}}{\partial t}}+({\vec {u}}\cdot {\vec {\nabla }}){\vec {u}}&=\nu \Delta {\vec {u}}+{\frac {{\vec {F_{\text{ext}}}}-{\vec {\nabla }}p}{\rho }}\\{\vec {\nabla }}\cdot {\vec {u}}&=0\end{aligned}}}$$where ${\textstyle {\vec {u}}(t,x,y,z)}$ is the fluid velocity, ${\textstyle p}$ is the pressure, ${\textstyle \rho }$ the density, ${\textstyle \nu }$ the viscosity, and ${\textstyle {\vec {F_{\text{ext}}}}}$ the net external force on each fluid particle (typically gravity). Under typical conditions, however, the movement of waves is described by Airy wave theory, which posits that

• fluid motion is roughly irrotational,
• pressure is approximately constant at the water surface, and
• the seabed depth is approximately constant.

In situations relevant for energy harvesting from ocean waves these assumptions are usually valid.

Airy equations

The first condition implies that the motion can be described by a velocity potential ${\textstyle \phi (t,x,y,z)}$:$${\displaystyle {{\vec {\nabla }}\times {\vec {u}}={\vec {0}}}\Leftrightarrow {{\vec {u}}={\vec {\nabla }}\phi }{\text{,}}}$$which must satisfy the Laplace equation,$${\displaystyle \nabla ^{2}\phi =0{\text{.}}}$$In an ideal flow, the viscosity is negligible and the only external force acting on the fluid is the earth gravity ${\displaystyle {\vec {F_{\text{ext}}}}=(0,0,-\rho g)}$. In those circumstances, the Navier-Stokes equations reduces to $${\displaystyle {\partial {\vec {\nabla }}\phi \over \partial t}+{1 \over 2}{\vec {\nabla }}{\bigl (}{\vec {\nabla }}\phi {\bigr )}^{2}=-{1 \over \rho }\cdot {\vec {\nabla }}p+{1 \over \rho }{\vec {\nabla }}{\bigl (}\rho gz{\bigr )},}$$which integrates (spatially) to the Bernoulli conservation law:$${\displaystyle {\partial \phi \over \partial t}+{1 \over 2}{\bigl (}{\vec {\nabla }}\phi {\bigr )}^{2}+{1 \over \rho }p+gz=({\text{const}}){\text{.}}}$$

Linear potential flow theory

When considering small amplitude waves and motions, the quadratic term ${\textstyle \left({\vec {\nabla }}\phi \right)^{2}}$ can be neglected, giving the linear Bernoulli equation,$${\displaystyle {\partial \phi \over \partial t}+{1 \over \rho }p+gz=({\text{const}}){\text{.}}}$$and third Airy assumptions then imply$${\displaystyle {\begin{aligned}&{\partial ^{2}\phi \over \partial t^{2}}+g{\partial \phi \over \partial z}=0\quad \quad \quad ({\text{surface}})\\&{\partial \phi \over \partial z}=0{\phantom {{\partial ^{2}\phi \over \partial t^{2}}+{}}}\,\,\quad \quad \quad ({\text{seabed}})\end{aligned}}}$$These constraints entirely determine sinusoidal wave solutions of the form $${\displaystyle \phi =A(z)\sin {\!(kx-\omega t)}{\text{,}}}$$where ${\displaystyle k}$ determines the wavenumber of the solution and ${\displaystyle A(z)}$ and ${\displaystyle \omega }$ are determined by the boundary constraints (and ${\displaystyle k}$). Specifically,$${\displaystyle {\begin{aligned}&A(z)={gH \over 2\omega }{\cosh(k(z+h)) \over \cosh(kh)}\\&\omega =gk\tanh(kh){\text{.}}\end{aligned}}}$$The surface elevation ${\displaystyle \eta }$ can then be simply derived as $${\displaystyle \eta =-{1 \over g}{\partial \phi \over \partial t}={H \over 2}\cos(kx-\omega t){\text{:}}}$$a plane wave progressing along the x-axis direction.

Consequences

Oscillatory motion is highest at the surface and diminishes exponentially with depth. However, for standing waves (clapotis) near a reflecting coast, wave energy is also present as pressure oscillations at great depth, producing microseisms. Pressure fluctuations at greater depth are too small to be interesting for wave power conversion.

The behavior of Airy waves offers two interesting regimes: water deeper than half the wavelength, as is common in the sea and ocean, and shallow water, with wavelengths larger than about twenty times the water depth. Deep waves are dispersionful: Waves of long wavelengths propagate faster and tend to outpace those with shorter wavelengths. Deep-water group velocity is half the phase velocity. Shallow water waves are dispersionless: group velocity is equal to phase velocity, and wavetrains propagate undisturbed.

The following table summarizes the behavior of waves in the various regimes:

Airy gravity waves on the surface of deep water, shallow water, or intermediate depth

quantity	symbol	units	deep water (h > 1⁄2 λ)	shallow water (h < 0.05 λ)	intermediate depth (all λ and h)
phase velocity	${\displaystyle c_{p}={\frac {\lambda }{T}}={\frac {\omega }{k}}}$	m / s	${\displaystyle {\frac {g}{2\pi }}T}$	${\displaystyle {\sqrt {gh}}}$	${\displaystyle {\sqrt {{\frac {g\lambda }{2\pi }}\tanh \left({\frac {2\pi h}{\lambda }}\right)}}}$
group velocity	${\displaystyle c_{g}=c_{p}^{2}{\frac {\partial \left(\lambda /c_{p}\right)}{\partial \lambda }}={\frac {\partial \omega }{\partial k}}}$	m / s	${\displaystyle {\frac {g}{4\pi }}T}$	${\displaystyle {\sqrt {gh}}}$	${\displaystyle {\frac {1}{2}}c_{p}\left(1+{\frac {4\pi h}{\lambda }}{\frac {1}{\sinh \left({\frac {4\pi h}{\lambda }}\right)}}\right)}$
ratio	${\displaystyle {\frac {c_{g}}{c_{p}}}}$	–	${\displaystyle {\frac {1}{2}}}$	${\displaystyle 1}$	${\displaystyle {\frac {1}{2}}\left(1+{\frac {4\pi h}{\lambda }}{\frac {1}{\sinh \left({\frac {4\pi h}{\lambda }}\right)}}\right)}$
wavelength	${\displaystyle \lambda }$	m	${\displaystyle {\frac {g}{2\pi }}T^{2}}$	${\displaystyle T{\sqrt {gh}}}$	for given period T, the solution of:   ${\displaystyle \left({\frac {2\pi }{T}}\right)^{2}={\frac {2\pi g}{\lambda }}\tanh \left({\frac {2\pi h}{\lambda }}\right)}$
general
wave energy density	${\displaystyle E}$	J / m	${\displaystyle {\frac {1}{16}}\rho gH_{m0}^{2}}$
wave energy flux	${\displaystyle P}$	W / m	${\displaystyle E\;c_{g}}$
angular frequency	${\displaystyle \omega }$	rad / s	${\displaystyle {\frac {2\pi }{T}}}$
wavenumber	${\displaystyle k}$	rad / m	${\displaystyle {\frac {2\pi }{\lambda }}}$

Wave power formula

In deep water where the water depth is larger than half the wavelength, the wave energy flux is

${\displaystyle P={\frac {\rho g^{2}}{64\pi }}H_{m0}^{2}T_{e}\approx \left(0.5{\frac {\text{kW}}{{\text{m}}^{3}\cdot {\text{s}}}}\right)H_{m0}^{2}\;T_{e},}$

with P the wave energy flux per unit of wave-crest length, H_m0 the significant wave height, T_e the wave energy period, ρ the water density and g the acceleration by gravity. The above formula states that wave power is proportional to the wave energy period and to the square of the wave height. When the significant wave height is given in metres, and the wave period in seconds, the result is the wave power in kilowatts (kW) per metre of wavefront length.

For example, consider moderate ocean swells, in deep water, a few km off a coastline, with a wave height of 3 m and a wave energy period of 8 s. Solving for power produces

${\displaystyle P\approx 0.5{\frac {\text{kW}}{{\text{m}}^{3}\cdot {\text{s}}}}(3\cdot {\text{m}})^{2}(8\cdot {\text{s}})\approx 36{\frac {\text{kW}}{\text{m}}},}$

or 36 kilowatts of power potential per meter of wave crest.

In major storms, the largest offshore sea states have significant wave height of about 15 meters and energy period of about 15 seconds. According to the above formula, such waves carry about 1.7 MW of power across each meter of wavefront.

An effective wave power device captures a significant portion of the wave energy flux. As a result, wave heights diminish in the region behind the device.

Energy and energy flux

In a sea state, the mean energy density per unit area of gravity waves on the water surface is proportional to the wave height squared, according to linear wave theory:

${\displaystyle E={\frac {1}{16}}\rho gH_{m0}^{2},}$

where E is the mean wave energy density per unit horizontal area (J/m), the sum of kinetic and potential energy density per unit horizontal area. The potential energy density is equal to the kinetic energy, both contributing half to the wave energy density E, as can be expected from the equipartition theorem.

The waves propagate on the surface, where crests travel with the phase velocity while the energy is transported horizontally with the group velocity. The mean transport rate of the wave energy through a vertical plane of unit width, parallel to a wave crest, is the energy flux (or wave power, not to be confused with the output produced by a device), and is equal to:

${\displaystyle P=E\,c_{g},}$ with c_g the group velocity (m/s).

Due to the dispersion relation for waves under gravity, the group velocity depends on the wavelength λ, or equivalently, on the wave period T.

Wave height is determined by wind speed, the length of time the wind has been blowing, fetch (the distance over which the wind excites the waves) and by the bathymetry (which can focus or disperse the energy of the waves). A given wind speed has a matching practical limit over which time or distance do not increase wave size. At this limit the waves are said to be "fully developed". In general, larger waves are more powerful but wave power is also determined by wavelength, water density, water depth and acceleration of gravity.

Wave energy converters

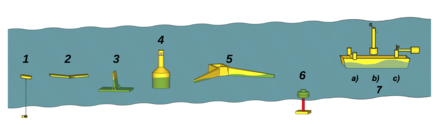
Wave energy converters (WECs) are generally categorized by the method, by location and by the power take-off system. Locations are shoreline, nearshore and offshore. Types of power take-off include: hydraulic ram, elastomeric hose pump, pump-to-shore, hydroelectric turbine, air turbine, and linear electrical generator.

The four most common approaches are:

• point absorber buoys
• surface attenuators
• oscillating water columns
• overtopping devices

Point absorber buoy

This device floats on the surface, held in place by cables connected to the seabed. The point-absorber has a device width much smaller than the incoming wavelength λ. Energy is absorbed by radiating a wave with destructive interference to the incoming waves. Buoys use the swells' rise and fall to generate electricity directly via linear generators, generators driven by mechanical linear-to-rotary converters, or hydraulic pumps. Energy extracted from waves may affect the shoreline, implying that sites should remain well offshore.

One point absorber design tested at commercial scale by CorPower features a negative spring that improves performance and protects the buoy in very large waves. It also has an internal pneumatic cylinder that keeps the buoy at a fixed distance from the seabed regardless of the state of the tide. Under normal operating conditions, the buoy bobs up and down at double the wave amplitude by adjusting the phase of its movements. It rises with a slight delay from the wave, which allows it to extract more energy. The firm claimed a 300% increase (600 kW) in power generation compared to a buoy without phase adjustments in tests completed in 2024.

Surface attenuator

These devices use multiple floating segments connected to one another. They are oriented perpendicular to incoming waves. A flexing motion is created by swells, and that motion drives hydraulic pumps to generate electricity. The Pelamis Wave Energy Converter is one of the more well-known attenuator concepts, although this is no longer being developed.

Oscillating wave surge converter

These devices typically have one end fixed to a structure or the seabed while the other end is free to move. Energy is collected from the relative motion of the body compared to the fixed point. Converters often come in the form of floats, flaps, or membranes. Some designs incorporate parabolic reflectors to focus energy at the point of capture. These systems capture energy from the rise and fall of waves.

Oscillating water column

Oscillating water column devices can be located onshore or offshore. Swells compress air in an internal chamber, forcing air through a turbine to create electricity. Significant noise is produced as air flows through the turbines, potentially affecting nearby birds and marine organisms. Marine life could possibly become trapped or entangled within the air chamber. It draws energy from the entire water column.

Overtopping device

Overtopping devices are long structures that use wave velocity to fill a reservoir to a greater water level than the surrounding ocean. The potential energy in the reservoir height is captured with low-head turbines. Devices can be on- or offshore.

Submerged pressure differential

Submerged pressure differential based converters use flexible (typically reinforced rubber) membranes to extract wave energy. These converters use the difference in pressure at different locations below a wave to produce a pressure difference within a closed power take-off hydraulic system. This pressure difference is usually used to produce flow, which drives a turbine and electrical generator. Submerged pressure differential converters typically use flexible membranes as the working surface between the water and the power take-off. Membranes are pliant and low mass, which can strengthen coupling with the wave's energy. Their pliancy allows large changes in the geometry of the working surface, which can be used to tune the converter for specific wave conditions and to protect it from excessive loads in extreme conditions.

A submerged converter may be positioned either on the seafloor or in midwater. In both cases, the converter is protected from water impact loads which can occur at the free surface. Wave loads also diminish in non-linear proportion to the distance below the free surface. This means that by optimizing depth, protection from extreme loads and access to wave energy can be balanced.

Floating in-air converters

Floating in-air converters potentially offer increased reliability because the device is located above the water, which also eases inspection and maintenance. Examples of different concepts of floating in-air converters include:

• roll damping energy extraction systems with turbines in compartments containing sloshing water
• horizontal axis pendulum systems
• vertical axis pendulum systems

Submerged wave energy converters

In early 2024, a fully submerged wave energy converter using point absorber-type wave energy technology was approved in Spain. The converter includes a buoy that is moored to the bottom and situated below the surface, out of sight of people and away from storm waves.

Environmental effects

Common environmental concerns associated with marine energy include:

• The effects of electromagnetic fields and underwater noise;
• Physical presence's potential to alter the behavior of marine mammals, fish, and seabirds with attraction, avoidance, entanglement
• Potential effect on marine processes such as sediment transport and water quality.
• Foundation/mooring systems can affect benthic organisms via entanglement/entrapment
• Electromotive force effects produced from subsea power cables.
• Minor collision risk
• Artificial reef accumulation near fixed installations
• Potential disuption to roosting sites

The Tethys database provides access to scientific literature and general information on the potential environmental effects of ocean current energy.

Potential

Wave energy's worldwide theoretical potential has been estimated to be greater than 2 TW. Locations with the most potential for wave power include the western seaboard of Europe, the northern coast of the UK, and the Pacific coastlines of North and South America, Southern Africa, Australia, and New Zealand. The north and south temperate zones have the best sites for capturing wave power. The prevailing westerlies in these zones blow strongest in winter.

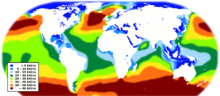
The National Renewable Energy Laboratory (NREL) estimated the theoretical wave energy potential for various countries. It estimated that the US' potential was equivalent to 1170 TWh per year or almost 1/3 of the country's electricity consumption. The Alaska coastline accounted for ~50% of the total.

The technical and economical potential will be lower than the given values for the theoretical potential.

Challenges

This section needs expansion with: what are the main technical difficulties?. You can help by adding to it. (February 2023)

Environmental impacts must be addressed. Socio-economic challenges include the displacement of commercial and recreational fishermen, and may present navigation hazards. Supporting infrastructure, such as grid connections, must be provided. Commercial WECs have not always been successful. In 2019, for example, Seabased Industries AB in Sweden was liquidated due to "extensive challenges in recent years, both practical and financial".

Current wave power generation technology is subject to many technical limitations. These limitations stem from the complex and dynamic nature of ocean waves, which require robust and efficient technology to capture the energy. Challenges include designing and building wave energy devices that can withstand the corrosive effects of saltwater, harsh weather conditions, and extreme wave forces. Additionally, optimizing the performance and efficiency of wave energy converters, such as oscillating water column (OWC) devices, point absorbers, and overtopping devices, requires overcoming engineering complexities related to the dynamic and variable nature of waves. Furthermore, developing effective mooring and anchoring systems to keep wave energy devices in place in the harsh ocean environment, and developing reliable and efficient power take-off mechanisms to convert the captured wave energy into electricity, are also technical challenges in wave power generation. As the wave energy dissipation by a submerged flexible mound breakwater is greater than that of a rigid submerged structure, greater wave energy dissipation is expected due to highly deformed shape of the structure.

Wave farms

A wave farm (wave power farm or wave energy park) is a group of colocated wave energy devices. The devices interact hydrodynamically and electrically, according to the number of machines, spacing and layout, wave climate, coastal and benthic geometry, and control strategies. The design process is a multi-optimization problem seeking high power production, low costs and limited power fluctuations. Nearshore wave farms have substantial impact on beach dynamics. For instance, wave farms significantly reduce erosion which demonstrates that this synergy between coastal protection and energy production enhances the economic viability of wave energy. Additional research finds that wave farms located near lagoons can potentially provide effective coastal protection during maritime spatial planning.

Gallery of wave energy installations

• Pelamis Wave Energy Converter on site at the European Marine Energy Centre (EMEC), in 2008.
• Azura at the US Navy’s Wave Energy Test Site (WETS) on Oahu.
• The AMOG Wave Energy Converter (WEC), in operation off SW England (2019).
• The mWave converter by Bombora Wave Power.
• CalWave Power Technologies, Inc. wave energy converter in California.

Patents

• WIPO patent application WO2016032360 — 2016 Pumped-storage system – "Pressure buffering hydro power" patent application
• U.S. patent 8,806,865 — 2011 Ocean wave energy harnessing device – Pelamis/Salter's Duck Hybrid patent
• U.S. patent 3,928,967 — 1974 Apparatus and method of extracting wave energy – The original "Salter's Duck" patent
• U.S. patent 4,134,023 — 1977 Apparatus for use in the extraction of energy from waves on water – Salter's method for improving "duck" efficiency
• U.S. patent 6,194,815 — 1999 Piezoelectric rotary electrical energy generator
• U.S. patent 1,930,958 — 1932 Wave Motor - Parsons Ocean Power Plant - Herring Cove Nova Scotia - March 1925. The world's first commercial plant to convert ocean wave energy into electrical power. Designer - Osborne Havelock Parsons - born in 1873 Petitcodiac, New Brunswick.
• Wave energy converters utilizing pressure differences US 20040217597 A1 — 2004 Wave energy converters utilizing pressure differences

A UK-based company has developed a Waveline Magnet that can achieve a levelized cost of electricity of £0.01/kWh with minimal levels of maintenance.

See also

• List of wave power projects
• List of wave power stations
• Wave power in Australia
• Wave power in New Zealand
• Wave power in Scotland
• Wave power in the United States
• Wave power ship
• WavePiston
• Marine energy
• Tidal power
• Ocean thermal energy conversion
• Osmotic power
• Office of Energy Efficiency and Renewable Energy (OEERE)
• World energy consumption

Notes

1. For determining the group velocity the angular frequency ω is considered as a function of the wavenumber k, or equivalently, the period T as a function of the wavelength λ.
2. The energy flux is ${\displaystyle P={\tfrac {1}{16}}\rho gH_{m0}^{2}c_{g},}$ with ${\displaystyle c_{g}}$ the group velocity, see Herbich, John B. (2000). Handbook of coastal engineering. McGraw-Hill Professional. A.117, Eq. (12). ISBN 978-0-07-134402-9. The group velocity is ${\displaystyle c_{g}={\tfrac {g}{4\pi }}T}$, see the collapsed table "Properties of gravity waves on the surface of deep water, shallow water and at intermediate depth, according to linear wave theory" in the section "Wave energy and wave energy flux" below.
3. Here, the factor for random waves is 1⁄16, as opposed to 1⁄8 for periodic waves – as explained hereafter. For a small-amplitude sinusoidal wave ${\textstyle \eta =a\cos 2\pi \left({\frac {x}{\lambda }}-{\frac {t}{T}}\right)}$ with wave amplitude ${\displaystyle a,}$ the wave energy density per unit horizontal area is ${\textstyle E={\frac {1}{2}}\rho ga^{2},}$ or ${\textstyle E={\frac {1}{8}}\rho gH^{2}}$ using the wave height ${\textstyle H=2a}$ for sinusoidal waves. In terms of the variance of the surface elevation ${\textstyle m_{0}=\sigma _{\eta }^{2}={\overline {(\eta -{\bar {\eta }})^{2}}}={\frac {1}{2}}a^{2},}$ the energy density is ${\textstyle E=\rho gm_{0}}$. Turning to random waves, the last formulation of the wave energy equation in terms of ${\textstyle m_{0}}$ is also valid (Holthuijsen, 2007, p. 40), due to Parseval's theorem. Further, the significant wave height is defined as ${\textstyle H_{m0}=4{\sqrt {m_{0}}}}$, leading to the factor 1⁄16 in the wave energy density per unit horizontal area.

References

1. ^ Phillips, O.M. (1977). The dynamics of the upper ocean (2nd ed.). Cambridge University Press. ISBN 978-0-521-29801-8.
2. Christine Miller (August 2004). "Wave and Tidal Energy Experiments in San Francisco and Santa Cruz". Archived from the original on October 2, 2008. Retrieved August 16, 2008.
3. ^ "Wave energy and its utilization". Slideshare. June 1, 1999. Retrieved April 28, 2023.
4. "World's first commercial wave power station activated in Scotland". Archived from the original on August 5, 2018. Retrieved June 5, 2018.
5. Joao Lima. Babcock, EDP and Efacec to Collaborate on Wave Energy projects Archived September 24, 2015, at the Wayback Machine Bloomberg, September 23, 2008.
6. Falcão, António F. de O. (April 1, 2010). "Wave energy utilization: A review of the technologies". Renewable and Sustainable Energy Reviews. 14 (3): 899–918. Bibcode:2010RSERv..14..899F. doi:10.1016/j.rser.2009.11.003. ISSN 1364-0321.
7. Madan, D.; Rathnakumar, P.; Marichamy, S.; Ganesan, P.; Vinothbabu, K.; Stalin, B. (October 21, 2020), "A Technological Assessment of the Ocean Wave Energy Converters", Advances in Industrial Automation and Smart Manufacturing, Lecture Notes in Mechanical Engineering, Singapore: Springer Singapore, pp. 1057–1072, doi:10.1007/978-981-15-4739-3_91, ISBN 978-981-15-4738-6, S2CID 226322561, retrieved June 2, 2022
8. ^ Clément; et al. (2002). "Wave energy in Europe: current status and perspectives". Renewable and Sustainable Energy Reviews. 6 (5): 405–431. Bibcode:2002RSERv...6..405C. doi:10.1016/S1364-0321(02)00009-6.
9. "The Development of Wave Power" (PDF). Archived from the original (PDF) on July 27, 2011. Retrieved December 18, 2009.
10. Morris-Thomas; Irvin, Rohan J.; Thiagarajan, Krish P.; et al. (2007). "An Investigation Into the Hydrodynamic Efficiency of an Oscillating Water Column". Journal of Offshore Mechanics and Arctic Engineering. 129 (4): 273–278. doi:10.1115/1.2426992.
11. "Wave Energy Research and Development at JAMSTEC". Archived from the original on July 1, 2008. Retrieved December 18, 2009.
12. Farley, F. J. M. & Rainey, R. C. T. (2006). "Radical design options for wave-profiling wave energy converters" (PDF). International Workshop on Water Waves and Floating Bodies. Loughborough. Archived (PDF) from the original on July 26, 2011. Retrieved December 18, 2009.
13. "Edinburgh Wave Energy Project" (PDF). University of Edinburgh. Archived from the original (PDF) on October 1, 2006. Retrieved October 22, 2008.
14. Falnes, J. (2007). "A review of wave-energy extraction". Marine Structures. 20 (4): 185–201. Bibcode:2007MaStr..20..185F. doi:10.1016/j.marstruc.2007.09.001.
15. "Our history". Retrieved April 28, 2023.
16. Aderinto, Tunde and Li, Hua (2019). "Review on power performance and efficiency of wave energy converters". Energies. 12 (22): 4329. doi:10.3390/en12224329.{{cite journal}}: CS1 maint: multiple names: authors list (link)
17. "Ocean Energy Teams Compete for $16 Million Scotland Prize". National geographic. September 7, 2012. Archived from the original on September 11, 2022.
18. Scott Macnab (November 2, 2017). "Government's £200m wave energy plan undermined by failures". The Scotsman. Archived from the original on December 5, 2017. Retrieved December 5, 2017.
19. Wave Energy Bill Approved by U.S. House Science Committee Archived May 25, 2018, at the Wayback Machine June 18, 2007
20. DOE announces first marine renewable energy grants Archived 2004-07-27 at the Wayback Machine September 30, 2008
21. "Ocean energy". Retrieved April 28, 2023.
22. "Projects to unlock the potential of marine wave energy". March 24, 2021. Retrieved April 28, 2023.
23. "Wave energy Scotland". Retrieved April 28, 2023.
24. Numerical modelling of wave energy converters : state-of-the-art techniques for single devices and arrays. Matt Folley. London, UK. 2016. ISBN 978-0-12-803211-4. OCLC 952708484.{{cite book}}: CS1 maint: location missing publisher (link) CS1 maint: others (link)
25. R. G. Dean & R. A. Dalrymple (1991). Water wave mechanics for engineers and scientists. Advanced Series on Ocean Engineering. Vol. 2. World Scientific, Singapore. ISBN 978-981-02-0420-4. See page 64–65.
26. ^ Goda, Y. (2000). Random Seas and Design of Maritime Structures. World Scientific. ISBN 978-981-02-3256-6.
27. Figure 6 from: Wiegel, R.L.; Johnson, J.W. (1950), "Elements of wave theory", Proceedings 1st International Conference on Coastal Engineering, Long Beach, California: ASCE, pp. 5–21, doi:10.9753/icce.v1.2
28. Tucker, M.J.; Pitt, E.G. (2001). "2". In Bhattacharyya, R.; McCormick, M.E. (eds.). Waves in ocean engineering (1st ed.). Oxford: Elsevier. pp. 35–36. ISBN 978-0080435664.
29. "Wave Power". University of Strathclyde. Archived from the original on December 26, 2008. Retrieved November 2, 2008.
30. ^ "Wave Energy Potential on the U.S. Outer Continental Shelf" (PDF). United States Department of the Interior. Archived from the original (PDF) on July 11, 2009. Retrieved October 17, 2008.
31. Academic Study: Matching Renewable Electricity Generation with Demand: Full Report Archived November 14, 2011, at the Wayback Machine. Scotland.gov.uk.
32. Holthuijsen, Leo H. (2007). Waves in oceanic and coastal waters. Cambridge: Cambridge University Press. ISBN 978-0-521-86028-4.
33. Reynolds, O. (1877). "On the rate of progression of groups of waves and the rate at which energy is transmitted by waves". Nature. 16 (408): 343–44. Bibcode:1877Natur..16R.341.. doi:10.1038/016341c0.
    Lord Rayleigh (J. W. Strutt) (1877). "On progressive waves". Proceedings of the London Mathematical Society. 9 (1): 21–26. doi:10.1112/plms/s1-9.1.21. Reprinted as Appendix in: Theory of Sound 1, MacMillan, 2nd revised edition, 1894.
34. Embedded Shoreline Devices and Uses as Power Generation Sources Kimball, Kelly, November 2003
35. "Seabased AB wave energy technology". Archived from the original on October 10, 2017. Retrieved October 10, 2017.
36. "PowerBuoy Technology — Ocean Power Technologies". Archived from the original on October 10, 2017. Retrieved October 10, 2017.
37. "Perth Wave Energy Project – Carnegie's CETO Wave Energy technology". Archived from the original on October 11, 2017. Retrieved October 10, 2017.
38. ^ "Tethys". Archived from the original on May 20, 2014. Retrieved April 21, 2014.
39. Blain, Loz (March 7, 2024). "Video: Wave-amplifying generator bounces twice as high as the swells". New Atlas. Retrieved April 12, 2024.
40. "Wave power firm Pelamis calls in administrators". BBC News. November 21, 2014. Retrieved April 13, 2024.
41. McCormick, Michael E.; Ertekin, R. Cengiz (2009). "Renewable sea power: Waves, tides, and thermals – new research funding seeks to put them to work for us". Mechanical Engineering. 131 (5). ASME: 36–39. doi:10.1115/1.2009-MAY-4.
42. "Extracting Energy From Ocean Waves". Archived from the original on August 15, 2015. Retrieved April 23, 2015.
43. Blain, Loz (August 1, 2022). "Blowhole wave energy generator exceeds expectations in 12-month test". New Atlas. Retrieved August 8, 2022.
44. Kurniawan, Adi; Greaves, Deborah; Chaplin, John (December 8, 2014). "Wave energy devices with compressible volumes". Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 470 (2172): 20140559. Bibcode:2014RSPSA.47040559K. doi:10.1098/rspa.2014.0559. ISSN 1364-5021. PMC 4241014. PMID 25484609.
45. ^ Paleja, Ameya (April 18, 2024). "Spain set to get table-top-like submerged sea wave energy converter". Interesting Engineering. Archived from the original on April 22, 2024.
46. "Tethys". Tethys. PNNL.
47. Gunn, Kester; Stock-Williams, Clym (August 2012). "Quantifying the global wave power resource". Renewable Energy. 44. Elsevier: 296–304. Bibcode:2012REne...44..296G. doi:10.1016/j.renene.2012.01.101.
48. "Ocean Wave Energy | BOEM". www.boem.gov. Archived from the original on March 26, 2019. Retrieved March 10, 2019.
49. "Renewable Energy Economic Potential". www.nrel.gov. Retrieved May 2, 2023.
50. Teske, S.; Nagrath, K.; Morris, T.; Dooley, K. (2019). "Renewable Energy Resource Assessment". In Teske, S. (ed.). Achieving the Paris Climate Agreement Goals. Springer. pp. 161–173. doi:10.1007/978-3-030-05843-2_7. ISBN 978-3-030-05842-5. S2CID 134370729.
51. Marine Renewable Energy Programme Archived August 3, 2011, at the Wayback Machine, NERC Retrieved August 1, 2011
52. Steven Hackett:Economic and Social Considerations for Wave Energy Development in California CEC Report Nov 2008 Archived May 26, 2009, at the Wayback Machine Ch2, pp22-44 California Energy Commission|Retrieved December 14, 2008
53. Gallucci, M. (December 2019). "At last, wave energy tech plugs into the grid - [News]". IEEE Spectrum. 56 (12): 8–9. doi:10.1109/MSPEC.2019.8913821. ISSN 1939-9340.
54. "Seabased Closes Production Facility in Sweden". marineenergy.biz. January 2019. Retrieved December 12, 2019.
55. Singh, Rajesh; Kumar, Suresh; Gehlot, Anita; Pachauri, Rupendra (February 2018). "An imperative role of sun trackers in photovoltaic technology: A review". Renewable and Sustainable Energy Reviews. 82: 3263–3278. Bibcode:2018RSERv..82.3263S. doi:10.1016/j.rser.2017.10.018.
56. Felix, Angélica; V. Hernández-Fontes, Jassiel; Lithgow, Débora; Mendoza, Edgar; Posada, Gregorio; Ring, Michael; Silva, Rodolfo (July 2019). "Wave Energy in Tropical Regions: Deployment Challenges, Environmental and Social Perspectives". Journal of Marine Science and Engineering. 7 (7): 219. Bibcode:2019JMSE....7..219F. doi:10.3390/jmse7070219. ISSN 2077-1312.
57. Xamán, J.; Rodriguez-Ake, A.; Zavala-Guillén, I.; Hernández-Pérez, I.; Arce, J.; Sauceda, D. (April 2020). "Thermal performance analysis of a roof with a PCM-layer under Mexican weather conditions". Renewable Energy. 149: 773–785. Bibcode:2020REne..149..773X. doi:10.1016/j.renene.2019.12.084. S2CID 213903662.
58. Røe, Oluf Dimitri; Stella, Giulia Maria (2017), Testa, Joseph R. (ed.), "Malignant Pleural Mesothelioma: History, Controversy, and Future of a Man-Made Epidemic", Asbestos and Mesothelioma, Current Cancer Research, Cham: Springer International Publishing, pp. 73–101, doi:10.1007/978-3-319-53560-9_4, hdl:11250/2628134, ISBN 978-3-319-53558-6, retrieved April 18, 2023
59. Jafarzadeh, E., Kabiri-Samani, A., Mansourzadeh, S., & Bohluly, A. (2021). Experimental modeling of the interaction between waves and submerged flexible mound breakwaters. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 235(1), 127-141.
60. Giassi, Marianna; Göteman, Malin (April 2018). "Layout design of wave energy parks by a genetic algorithm". Ocean Engineering. 154: 252–261. Bibcode:2018OcEng.154..252G. doi:10.1016/j.oceaneng.2018.01.096. ISSN 0029-8018. S2CID 96429721.
61. Abanades, J.; Greaves, D.; Iglesias, G. (September 1, 2014). "Coastal defence through wave farms". Coastal Engineering. 91: 299–307. Bibcode:2014CoasE..91..299A. doi:10.1016/j.coastaleng.2014.06.009. hdl:10026.1/4556. ISSN 0378-3839. S2CID 35664931.
62. Onea, Florin; Rusu, Liliana; Carp, Gabriel Bogdan; Rusu, Eugen (March 2021). "Wave Farms Impact on the Coastal Processes—A Case Study Area in the Portuguese Nearshore". Journal of Marine Science and Engineering. 9 (3): 262. doi:10.3390/jmse9030262. ISSN 2077-1312.
63. FreePatentsOnline.com Wave energy converters utilizing pressure differences Archived October 31, 2014, at the Wayback Machine, April 11, 2004
64. "Wave magnets offer 'cheapest clean energy ever'". The Independent. August 31, 2022.

Further reading

• Cruz, Joao (2008). Ocean Wave Energy – Current Status and Future Prospects. Springer. ISBN 978-3-540-74894-6., 431 pp.
• Falnes, Johannes (2002). Ocean Waves and Oscillating Systems. Cambridge University Press. ISBN 978-0-521-01749-7., 288 pp.
• McCormick, Michael (2007). Ocean Wave Energy Conversion. Dover. ISBN 978-0-486-46245-5., 256 pp.
• Twidell, John; Weir, Anthony D.; Weir, Tony (2006). Renewable Energy Resources. Taylor & Francis. ISBN 978-0-419-25330-3., 601 pp.

External links

• Portal and Repository for Information on Marine Renewable Energy A network of databases providing broad access to marine energy information.
• Marine Energy Basics: Wave Energy Basic information about wave energy.
• Marine Energy Projects Database A database that provides up-to-date information on marine energy deployments in the U.S. and around the world.
• Tethys Database A database of information on potential environmental effects of marine energy and offshore wind energy development.
• Tethys Engineering Database A database of information on technical design and engineering of marine energy devices.
• Marine and Hydrokinetic Data Repository A database for all data collected by marine energy research and development projects funded by the U.S. Department of Energy.
• Wave Swell Energy video on YouTube
• Kate Galbraith (September 22, 2008). "Power From the Restless Sea Stirs the Imagination". The New York Times. Retrieved October 9, 2008.
• "Wave Power: The Coming Wave" from the Economist, June 5, 2008

v t e Marine energy
Wave power	List of wave power stations List of wave power projects Australia New Zealand United States Scotland
Tidal power	List of tidal power stations Tidal barrage Tidal stream generator Development of tidal stream generators
Other	List of offshore wind farms Marine current power Ocean thermal energy conversion Offshore construction Osmotic power
Energy portal Renewable energy portal Oceans portal Category

v t e Physical oceanography
Waves	Airy wave theory Ballantine scale Benjamin–Feir instability Boussinesq approximation Breaking wave Clapotis Cnoidal wave Cross sea Dispersion Edge wave Equatorial waves Gravity wave Green's law Infragravity wave Internal wave Iribarren number Kelvin wave Kinematic wave Longshore drift Luke's variational principle Mild-slope equation Radiation stress Rogue wave Rossby wave Rossby-gravity waves Sea state Seiche Significant wave height Soliton Stokes drift Stokes problem Stokes wave Swell Trochoidal wave Tsunami megatsunami Undertow Ursell number Wave action Wave base Wave height Wave nonlinearity Wave power Wave radar Wave setup Wave shoaling Wave turbulence Wave–current interaction Waves and shallow water one-dimensional Saint-Venant equations shallow water equations Wind fetch Wind setup Wind wave model
Circulation	Atmospheric circulation Baroclinity Boundary current Coriolis force Coriolis–Stokes force Craik–Leibovich vortex force Downwelling Eddy Ekman layer Ekman spiral Ekman transport El Niño–Southern Oscillation General circulation model Geochemical Ocean Sections Study Geostrophic current Global Ocean Data Analysis Project Gulf Stream Humboldt Current Hydrothermal circulation Langmuir circulation Longshore drift Loop Current Modular Ocean Model Ocean current Ocean dynamical thermostat Ocean dynamics Ocean gyre Overflow Princeton Ocean Model Rip current Subsurface ocean current Sverdrup balance Thermohaline circulation shutdown Upwelling Whirlpool Wind generated current World Ocean Circulation Experiment
Tides	Amphidromic point Earth tide Head of tide Internal tide Lunitidal interval Perigean spring tide Rip tide Rule of twelfths Slack tide Theory of tides Tidal bore Tidal force Tidal power Tidal race Tidal range Tidal resonance Tide gauge Tideline
Landforms	Abyssal fan Abyssal plain Atoll Bathymetric chart Carbonate platform Coastal geography Cold seep Continental margin Continental rise Continental shelf Contourite Guyot Hydrography Knoll Ocean bank Oceanic basin Oceanic plateau Oceanic trench Passive margin Seabed Seamount Submarine canyon Submarine volcano
Plate tectonics	Convergent boundary Divergent boundary Fracture zone Hydrothermal vent Marine geology Mid-ocean ridge Mohorovičić discontinuity Oceanic crust Outer trench swell Ridge push Seafloor spreading Slab pull Slab suction Slab window Subduction Transform fault Vine–Matthews–Morley hypothesis Volcanic arc
Ocean zones	Benthic Deep ocean water Deep sea Littoral Mesopelagic Oceanic Pelagic Photic Surf Swash
Sea level	Deep-ocean Assessment and Reporting of Tsunamis Global Sea Level Observing System North West Shelf Operational Oceanographic System Sea-level curve Sea level drop Sea level rise World Geodetic System
Acoustics	Deep scattering layer Ocean acoustic tomography Sofar bomb SOFAR channel Underwater acoustics
Satellites	Jason-1 OSTM/Jason-2 Jason-3
Related	Acidification Argo Benthic lander Color of water DSV Alvin Marginal sea Marine energy Marine pollution Mooring National Oceanographic Data Center Ocean Explorations Observations Reanalysis Ocean surface topography Ocean temperature Ocean thermal energy conversion Oceanography Outline of oceanography Pelagic sediment Sea surface microlayer Sea surface temperature Seawater Science On a Sphere Stratification Thermocline Underwater glider Water column World Ocean Atlas
Category Commons Oceans portal

• Renewable energy
• Energy
• Oceans

• Wave power
• Bright green environmentalism
• Energy conversion
• Power station technology
• Sustainable technologies