Weak beam dark field (WBDF) microscopy is a type of transmission electron microscopy (TEM) dark field imaging technique that allows for the visualization of crystal defects with high resolution and contrast. Specifically, the technique is mainly used to study crystal defects such as dislocations, stacking faults, and interfaces in crystalline materials. WBDF is a valuable tool for studying the microstructure of materials, as it can provide detailed information about the nature and distribution of defects in crystals. These characteristics can have a significant impact on material properties such as strength, ductility, and corrosion resistance.

WBDF works by using a selected weak first-order diffracted beam from the specimen. This is made possible by tilting the specimen to excite higher angle diffraction spots. The electrons diffracted by the crystal are selected using an objective aperture and selective aperture, which allows only a small fraction of the diffracted electrons to be imaged to the detector. The objective aperture controls size and angle of the incoming beam that is selecting the diffracted beam. The selective aperture selects the area where the diffraction comes from.
The WBDF image is able to highlight the location and type of crystal defects because the lattice bends back to Bragg's diffraction orientation near the defect core. The image can be further enhanced by tilting the crystal in different directions, which changes the orientation of the defects with respect to the electron beam. Under certain special diffraction conditions, dislocations can be imaged as narrow lines. The dislocation lines and Burgers vector can be determined for each dislocation. Also, the movement of dislocations in materials can be studied to determine mobility and subsequent material properties.
History
One of the first instances in literature which began the development of WBDF is from Hirsch, Howie, and Whelan in 1960. Their paper focused on applying kinematical theory to TEM imaging with emphasis on dislocation and defect imaging. Then, weak-beam techniques were further demonstrated from R. Gever, et al. The authors predicted that even when selecting a weak kinematical spot to form a TEM image, the fringe periodicity is the same as for bright field imaging. Further research into WBDF in 1969 demonstrated the technique's usefulness in imaging dislocations, as developed by Cockayne, Ray and Whelan. Since then, the technique has been widely used for analysis of dislocations and their interactions in crystalline samples.
WBDF theory
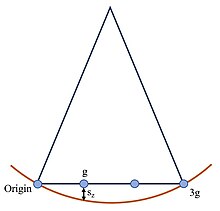
The weak beam dark field (WBDF) technique is based on using a diffracted beam with a large excitation error () to form an on-axis dark field image. To form an image, a first-order diffraction spot is selected while the sample is tilted to excite a higher angle, typically ~ 3g, diffraction spot. The WBDF g-ng condition means that 1g is the g vector used for forming the image and ng is the excited g vector. The specimen is tilted for the Ewald sphere to intersect the lattice at the origin and 3g as the figure shown. In the figure, , the excitation error, is made to be large such that the origin and the third order diffraction spot intersect with the Ewald sphere and are excited by the electron beam.
Note that under the two-beam conditions, the crystal is tilted in a way that there is only one strong diffracted beam at and all other diffracted beams are weak, ideally in a symmetric way around the direct beam. The intensity of the diffracted beam g in a perfect crystal can be written as an equation below:
Where is the sample thickness, is the extinction distance for diffraction vector g that depends on lattice parameters, atomic number, and the beam electron voltage used, and is the effective excitation error given by the equation:
For the WBDF technique, the excitation error can increase to about 0.2 as well as . When then , and this is known as the kinematical approximation. This theory leads to the main advantages seen from high-contrast defect images from WBDF. From the equation above, it is evident that the intensity decreases as increases.
In the areas of the sample without defects, diffraction intensity is weak which appears as dark areas in the image. However, near the dislocation core, the lattice plane bends back into Bragg's condition, which leads to a bright intensity peak observed as the dislocation line in the WBDF image. The main challenge presented with this technique is the ability to optimally adjust the tilt conditions to minimize the excitation error of the g reflection near the dislocation core so that a sharp dislocation line becomes visible. The exact value of g is not typically exactly 3g as proposed, and is dependent on material properties such as lattice parameter and TEM instrumentation used.
Dislocations in the sample, described by their Burgers vector b, will appear under the diffracted beam, vector g, when . This is important in WBDF imaging because one of the main advantages are the ability to qualitatively and quantitatively describe defects in a given material. There are three main mathematical methods to determine the dislocation peak position as described below.
1. Weak beam criterion: The diffracted beam has the largest intensity when or is zero.
Where z describes the direction of the electron beam and R is the displacement field around the dislocation.
2. Kinematical integral: There is maximized scattering from the transmitted to the diffracted beam when the kinematical integral equation below is maximized. This occurs near the dislocation core in the sample.
3. Computing the contrast: The width of the dislocation peak, represented by , can be narrowed according to the below equation. As the excitation error increases, the width of the dislocation peaks, and therefore the contrast seen in the image near the boundary between the dislocation and the background.
Weak beam dark field technique setup process
Setting up weak-beam dark-field imaging in transmission electron microscopy involves several steps, which may vary depending on the specific TEM instrument and the sample being analyzed. This may require further optimization and adjustment to achieve the desired image quality and contrast. The general steps include:
- Sample preparation: The sample should be prepared as a thin foil with thickness of a few tens of nanometers because the visibility of the image decreases as the sample thickness increases. However, the Kikuchi line might not be visible in the sample that is too thin.
- Sample orientation: The sample should first be aligned with the electron beam and tilted to a suitable angle to achieve the desired dark-field contrast.
- Tilt the sample to a low-index zone axis.
- Follow the Kikuchi lines to form the two-beam condition that is orienting the sample in bright field mode such that g is excited and is close to 0.
- Align the sample as if a dark field image were to be taken such that 1g aligns with the optical axis.
- Further tilt the sample to excite ng. The most common condition is g-3g. This will ensure the Bragg condition for the 3g reflection is satisfied. When looking at the diffraction pattern for confirmation, the 3g spot will become brighter and the 1g spot will become dimmer.
- Select the diffraction spot: The diffraction spot of 1g should be selected using an objective aperture to form a WBDF image with g-3g condition.
- Adjust the beam intensity and focus: The electron beam intensity and focus should be adjusted to achieve a high signal-to-noise ratio and a clear image. The beam should be focused on the sample and have a low enough intensity to avoid radiation damage.
- Acquire the image: The dark-field image can be acquired by selecting the WBDF mode and adjusting the camera parameters, such as exposure time, binning, and magnification, to optimize the image quality.
- Post-processing: The acquired image can be further processed using image analysis software to enhance the contrast, remove noise, and quantify the defect or feature of interest.
Comparison with other TEM imaging techniques

WBDF is often used in tandem with other TEM imaging techniques such as bright field (BF) and dark field (DF) imaging. These frequently used techniques similarly create an image from electrons that pass through and interact with the sample, however, the difference lies in the electrons which are selected to fall on the detector, and the degree of sample tilt. This control is allowed by the objective aperture. In BF imaging, the direct beam is selected to create the image, and in DF imaging, the scattered electron beams are used to create an image. Evidently, WBDF also uses scattered beams to form an image, but the difference between DF and WBDF comes from the degree of sample tilt and thus beam intensity on the first order diffraction spot. Shown below, a WBDF sample is tilted to excite the 3g diffraction spot to the Bragg condition, and the first-order diffraction spot is selected. This excitation is seen on the instrument as the diffraction spot getting brighter as the sample is tilted.
The analytical difference between WBDF and BF and DF imaging is that WBDF can achieve high-contrast images of defects and thickness changes in a sample. This is made possible by tilting the sample to increase the intensity of the beam on diffraction spots further from the direct beam. Due to the tilting and subsequent increase in excitation error, the electrons are treated in the kinematical approximation. This is the aspect of WBDF which sets it apart from BF and DF imaging, and allows for high contrast defect characterization. This process is described in more detail in the WBDF theory section.
In this approach, when the specimen is tilted far away from the Bragg condition as it is here, stronger peaks arise from defects in the material which are then able to be in the Bragg condition. In bright field imaging, the width of the dislocation features is larger than in WBDF because the core of the dislocation planes is what is locally bent back into the Bragg condition. When the angle is larger such as in WBDF, the planes need to bend more to satisfy the condition, decreasing the amount of the dislocation line that is shown in the subsequent image. As a result, the diffraction contrast increases as excitation error increases. The high contrast which is seen in WBDF images makes this technique especially useful in comparison to BF and DF since it provides more precise defect analysis. This can help to qualitatively and quantitatively analyze stacking faults, Burgers vectors, and even 3D reconstruction of dislocation networks in a specimen.
Advantages and limitations of WBDF
The main advantage of using WBDF is the ability to acquire high-contrast images of imperfect specimens for the purpose of studying defects in the material. This technique is not overly complex in its setup and can provide additional quantitative data for imaging a sample via TEM. Some examples of this include higher contrast images of thickness fringes, strain fields, and dissociated dislocations. For example, Feng et al. were able to use WBDF to show waveform contours in a barium titanate sample which demonstrated that strain contours were dependent on the stress state. The bright field images did not clearly show the strain field, while the WBDF was able to clearly show a pattern indicative of strain. In another example, Rakhmonov et al. used WBDF to study how dislocations interact with precipitates in an Al-Cu-Mn-Zr alloy crept at 300 °C, and they observed Orowan loops around precipitates.
The advantage of higher contrast thickness fringes is made possible by a large value which in turn makes be smaller and affects thickness periodicity. This is shown by the equation which comes from the weak beam approximation. When the extinction distance is larger, it increases the fringe separation and fringe width which thus increases the contrast that can be seen in thickness fringes and strain contrast.
Some limitations to WBDF are related to setup conditions, projection errors, and hardware limitations. For setup conditions, it is nontrivial to select the tilt, and therefore the excitation error, that is required for an optimal WBDF image. The 3g condition, in which the sample is tilted to make the 3g diffraction spot have a higher intensity, is a rule of thumb for attaining an image, but is not always true. The lattice parameter of the sample and the wavelength of electrons used can have an effect on the optimized value of s. A smaller value of s can be used to still attain defect information, but determining the tilt angle can take time and this can damage the defect structure of interest. A projection error is found in every WBDF image because the image of any defect is projected in the direction of the k-vector of the diffracted wave. This projection can change depending on the starting parameters used to form the image, and thus the analysis of the defect lines is not straightforward. Finally, there are limitations to the technique based on current instrument limitations such as the CCD cameras used, energy filtering of the electron source, and image processing which helps to rid noise from the image.
Examples of applications that use WBDF
Burgers Vector Determination in Perovskites
One example in literature of the utilization of WBDF microscopy is to quantitatively determine the direction of Burgers vectors for the purpose of characterizing dislocation types. In this case, the authors were able to determine screw and edge dislocations in a perovskite sample by imaging down multiple zone axes and calculating the Burgers vectors by counting the number of thickness fringes which terminate within the sample as opposed to at the edge of the sample. The high contrast from WBDF allows for easier determination of where the terminating edges are located.
Reconstruct three-dimensional dislocation array
The three-dimensional structure of dislocation arrays in GaN are able to be reconstructed by combining the weak beam dark field technique with tomography by Barnard, et al. The hetero-epitaxial GaN grown on sapphire with high dislocation along was used. The WBDF images were taken from 5° tilt to 120° tilt at constant excitation error, magnification, and rotation. Using back projections and sequentially iterated reconstruction technique, the reconstructed tomographic volume was achieved. The reconstructed volume is able to show threading dislocations, in-plane dislocation, and dislocation interactions.
Imaging of superdislocations and dislocation dynamics
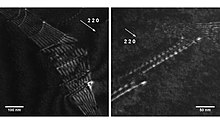
The advantages of WBDF are utilized to resolve dislocation dynamics in Fe2MnAl single crystals where superdislocations with 4-fold dissociation were imaged. The movement of a superdislocation at the nanometer scale can be seen in the image on the right. In the paper, Liao et al. show that the superdislocations glide in segments. The dislocations with screw character were shown to move in a “locking and unlocking” manner dependent on the pinning of the dislocation. The ability to see how dislocations move in a solid is fundamentally important to materials science and understanding yield stress anomaly of intermetallic compounds.
Future Directions for WBDF
The technique of WBDF can be further improved by TEM instrument advancements for the electron source and image processing. More specifically, field emission guns (FEGs) and the reduction of energy variation in the electron source can help to get even higher contrast images with higher resolution. Also, improvements to image detectors can help to reduce noise in the image which helps with quantitative analysis of defects in materials. These advancements would be especially helpful because of the weak beam condition. Improvements to contrast can also help with further analysis via high-throughput analysis of defects via computer modeling. This has been previously seen in literature which uses STEM images to train computers to find defects in a material that have high contrast and are more easily processed by the program.
See also
- Annular dark-field imaging
- Dark-field microscopy
- Electron diffraction
- Electron microscope
- Scanning transmission electron microscopy
- Transmission electron microscope
References
- ^ Williams, D. B., Carter, C. B., (2009) Transmission Electron Microscopy. Springer.
- Cockayne, DJH 1981 Weak-Beam Electron Microscopy Ann. Rev. Mater. Sci. 11, 75–95. A review of WB.
- Rakhmonov, J.U., Bahl, S., Shyam, A., Dunand, D.C. (2022) Cavitation-resistant intergranular precipitates enhance creep performance of θ’-strengthened Al-Cu based alloys. Acta Materialia, 228, 117788. doi:10.1016/j.actamat.2022.117788
- Hirsch, P. B., Howie, A., & Whelan, M. J.. (1960). A kinematical theory of diffraction contrast of electron transmission microscope images of dislocations and other defects. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 252(1017), 499–529. doi:10.1098/rsta.1960.0013
- Gevers, K., van Landuyt, J. and Amelinckx, S. (1967), Two Beam Kinematical Theory for the Diffraction of Electrons by Crystals with Stacking Faults. phys. stat. sol. (b), 21: 393-411. doi:10.1002/pssb.19670210140
- ^ Cockayne, D. J. H, Ray I. L. F., and Whelan, M. J. (1969) Investigations of dislocation strain fields using weak beams, The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics, 20:168, 1265-1270, doi:10.1080/14786436908228210
- P.J. Phillips, M.J. Mills & M. De Graef (2011) Systematic row and zone axis STEM defect image simulations, Philosophical Magazine, 91:16, 2081-2101, doi:10.1080/14786435.2010.547526
- Hirsch, P. B., Howie, A., & Whelan, M. J. (1960). A Kinematical Theory of Diffraction Contrast of Electron Transmission Microscope Images of Dislocations and other Defects. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 252(1017), 499–529. JSTOR 73192
- ^ Barnard, Jonathan & Sharp, Jo & Tong, Jenna & Midgley, P. (2006). Weak-beam dark-field electron tomography of dislocations in GaN. Journal of Physics: Conference Series. 26. 247-250. 10.1088/1742-6596/26/1/059.
- Cockayne, D. (1972). A Theoretical Analysis of the Weak-beam Method of Electron Microscopy. Zeitschrift für Naturforschung A, 27(3), 452-460. doi:10.1515/zna-1972-0313
- Miao, J., Singh, S., Tessmer, J., Shih, M., Ghazisaeidi, M., DeGraef, M., & Mills, M. (2018). Dislocation Characterization using Weak Beam Dark Field STEM Imaging. Microscopy and Microanalysis, 24(S1), 2202-2203. doi:10.1017/S1431927618011492
- Foll, H. , Carter, C.B., Wilkens, M. (1980) Weak-beam contrast of stacking faults in transmission electron microscopy, Physica Status Solidi a, 58(2), 393-407 doi:10.1002/pssa.2210580210
- ^ Miyajima, N., Walte, N., (2009) Burgers vector determination in deformed perovskite and post-perovskite of CaIrO3 using thickness fringes in weak-beam dark-field images, Ultramicroscopy, 109(6), 683-692, doi:10.1016/j.ultramic.2009.01.010
- ^ Barnard, J. S., Sharp, J., Tong, J. R., & Midgley, P. A.. (2006). Three-dimensional analysis of dislocation networks in GaN using weak-beam dark-field electron tomography. Philosophical Magazine, 86(29-31), 4901–4922. doi:10.1080/14786430600798839
- Feng, Q., McConville, C. J. (2005). Weak-Beam Dark-Field Microscopy of Complex Stress States in X7R-Type BaTiO3 Dielectric Core–Shell Structures, J. Am. Cer. Soc., 87(10), 1945-1951, doi:10.1111/j.1151-2916.2004.tb06345.x
- Rakhmonov, J., Bahl, S., Shyam, A., Dunand, D.C. (2022). Cavitation-resistant intergranular precipitates enhance creep performance of θ′-strengthened Al-Cu based alloys. Acta Materialia, 228 doi:10.1016/j.actamat.2022.117788
- Liao, Y., & Baker, I.. (2012). Study of yield stress anomaly of Fe2MnAl single crystal by in situ TEM straining. Philosophical Magazine, 92(8), 959–985. doi:10.1080/14786435.2011.637983
- Li, W., Field, K. G., & Morgan, D.. (2018). Automated defect analysis in electron microscopic images. NPJ Computational Materials, 4(1). doi:10.1038/s41524-018-0093-8
- This page was prepared in part for Northwestern University class MSE 460, taught by Professor Laurence D. Marks.
- Notes prepared by Professor Laurence D. Marks at Northwestern University.
| Electron microscopy | |||||||
|---|---|---|---|---|---|---|---|
| Basics | |||||||
| Electron interaction with matter | |||||||
| Instrumentation | |||||||
| Microscopes |
| ||||||
| Techniques |
| ||||||
| Others |
| ||||||
 ).
). and all other diffracted beams are weak, ideally in a symmetric way around the direct beam. The intensity of the diffracted beam g in a perfect crystal can be written as an equation below:
and all other diffracted beams are weak, ideally in a symmetric way around the direct beam. The intensity of the diffracted beam g in a perfect crystal can be written as an equation below:

 is the sample thickness,
is the sample thickness,  is the extinction distance for diffraction vector g that depends on
is the extinction distance for diffraction vector g that depends on  is the effective excitation error given by the equation:
is the effective excitation error given by the equation:

 as well as
as well as  then
then  , and this is known as the kinematical approximation. This theory leads to the main advantages seen from high-contrast defect images from WBDF. From the equation above, it is evident that the intensity decreases as
, and this is known as the kinematical approximation. This theory leads to the main advantages seen from high-contrast defect images from WBDF. From the equation above, it is evident that the intensity decreases as  . This is important in WBDF imaging because one of the main advantages are the ability to qualitatively and quantitatively describe defects in a given material. There are three main mathematical methods to determine the dislocation peak position as described below.
. This is important in WBDF imaging because one of the main advantages are the ability to qualitatively and quantitatively describe defects in a given material. There are three main mathematical methods to determine the dislocation peak position as described below.
 is zero.
is zero.

 , can be narrowed according to the below equation. As the excitation error increases, the width of the dislocation peaks, and therefore the contrast seen in the image near the boundary between the dislocation and the background.
, can be narrowed according to the below equation. As the excitation error increases, the width of the dislocation peaks, and therefore the contrast seen in the image near the boundary between the dislocation and the background.

 is close to 0.
is close to 0. be smaller and affects thickness periodicity. This is shown by the equation
be smaller and affects thickness periodicity. This is shown by the equation  which comes from the weak beam approximation. When the extinction distance is larger, it increases the fringe separation and fringe width which thus increases the contrast that can be seen in thickness fringes and strain contrast.
which comes from the weak beam approximation. When the extinction distance is larger, it increases the fringe separation and fringe width which thus increases the contrast that can be seen in thickness fringes and strain contrast.