Misplaced Pages

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (January 2023) This article provides insufficient context for those unfamiliar with the subject. Please help improve the article by providing more context for the reader. (January 2023) (Learn how and when to remove this message) (Learn how and when to remove this message)

The classical XY model (sometimes also called classical rotor (rotator) model or O(2) model) is a lattice model of statistical mechanics. In general, the XY model can be seen as a specialization of Stanley's n-vector model for n = 2.

Definition

Given a D-dimensional lattice Λ, per each lattice site j ∈ Λ there is a two-dimensional, unit-length vector s_j = (cos θ_j, sin θ_j)

The spin configuration, s = (s_j)_{j ∈ Λ} is an assignment of the angle −π < θ_j ≤ π for each j ∈ Λ.

Given a translation-invariant interaction J_ij = J(i − j) and a point dependent external field ${\displaystyle \mathbf {h} _{j}=(h_{j},0)}$, the configuration energy is

${\displaystyle H(\mathbf {s} )=-\sum _{i\neq j}J_{ij}\;\mathbf {s} _{i}\cdot \mathbf {s} _{j}-\sum _{j}\mathbf {h} _{j}\cdot \mathbf {s} _{j}=-\sum _{i\neq j}J_{ij}\;\cos(\theta _{i}-\theta _{j})-\sum _{j}h_{j}\cos \theta _{j}}$

The case in which J_ij = 0 except for ij nearest neighbor is called nearest neighbor case.

The configuration probability is given by the Boltzmann distribution with inverse temperature β ≥ 0:

${\displaystyle P(\mathbf {s} )={\frac {e^{-\beta H(\mathbf {s} )}}{Z}}\qquad Z=\int _{^{\Lambda }}\prod _{j\in \Lambda }d\theta _{j}\;e^{-\beta H(\mathbf {s} )}.}$

where Z is the normalization, or partition function. The notation ${\displaystyle \langle A(\mathbf {s} )\rangle }$ indicates the expectation of the random variable A(s) in the infinite volume limit, after periodic boundary conditions have been imposed.

Rigorous results

• The existence of the thermodynamic limit for the free energy and spin correlations were proved by Ginibre, extending to this case the Griffiths inequality.
• Using the Griffiths inequality in the formulation of Ginibre, Aizenman and Simon proved that the two point spin correlation of the ferromagnetics XY model in dimension D, coupling J > 0 and inverse temperature β is dominated by (i.e. has an upper bound given by) the two point correlation of the ferromagnetic Ising model in dimension D, coupling J > 0 and inverse temperature ⁠β/2⁠ $${\displaystyle \langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle _{J,2\beta }\leq \langle \sigma _{i}\sigma _{j}\rangle _{J,\beta }}$$ Hence the critical β of the XY model cannot be smaller than the double of the critical β of the Ising model $${\displaystyle \beta _{c}^{XY}\geq 2\beta _{c}^{\rm {Is}}}$$

One dimension

As in any 'nearest-neighbor' n-vector model with free (non-periodic) boundary conditions, if the external field is zero, there exists a simple exact solution. In the free boundary conditions case, the Hamiltonian is $${\displaystyle H(\mathbf {s} )=-J}$$ therefore the partition function factorizes under the change of coordinates $${\displaystyle \theta _{j}=\theta _{j}'+\theta _{j-1}\qquad j\geq 2}$$ This gives $${\displaystyle {\begin{aligned}Z&=\int _{-\pi }^{\pi }d\theta _{1}\cdots d\theta _{L}\;e^{\beta J\cos(\theta _{1}-\theta _{2})}\cdots e^{\beta J\cos(\theta _{L-1}-\theta _{L})}\\&=2\pi \prod _{j=2}^{L}\int _{-\pi }^{\pi }d\theta '_{j}\;e^{\beta J\cos \theta '_{j}}=(2\pi )\left^{L-1}=(2\pi )^{L}(I_{0}(\beta J))^{L-1}\end{aligned}}}$$ where ${\displaystyle I_{0}}$ is the modified Bessel function of the first kind. The partition function can be used to find several important thermodynamic quantities. For example, in the thermodynamic limit (${\displaystyle L\to \infty }$), the free energy per spin is $${\displaystyle f(\beta ,h=0)=-\lim _{L\to \infty }{\frac {1}{\beta L}}\ln Z=-{\frac {1}{\beta }}\ln}$$ Using the properties of the modified Bessel functions, the specific heat (per spin) can be expressed as $${\displaystyle {\frac {c}{k_{\rm {B}}}}=\lim _{L\to \infty }{\frac {1}{L(k_{\rm {B}}T)^{2}}}{\frac {\partial ^{2}}{\partial \beta ^{2}}}(\ln Z)=K^{2}\left(1-{\frac {\mu }{K}}-\mu ^{2}\right)}$$ where ${\displaystyle K=J/k_{\rm {B}}T}$, and ${\displaystyle \mu }$ is the short-range correlation function,

$${\displaystyle \mu (K)=\langle \cos(\theta -\theta ')\rangle ={\frac {I_{1}(K)}{I_{0}(K)}}}$$

Even in the thermodynamic limit, there is no divergence in the specific heat. Indeed, like the one-dimensional Ising model, the one-dimensional XY model has no phase transitions at finite temperature.

The same computation for periodic boundary condition (and still h = 0) requires the transfer matrix formalism, though the result is the same.

The partition function can be evaluated as $${\displaystyle Z={\text{tr}}\left\{\prod _{i=1}^{N}\oint d\theta _{i}e^{\beta J\cos(\theta _{i}-\theta _{i+1})}\right\}}$$ which can be treated as the trace of a matrix, namely a product of matrices (scalars, in this case). The trace of a matrix is simply the sum of its eigenvalues, and in the thermodynamic limit ${\displaystyle L\to \infty }$ only the largest eigenvalue will survive, so the partition function can be written as a repeated product of this maximal eigenvalue. This requires solving the eigenvalue problem $${\displaystyle \oint d\theta '\exp\{\beta J\cos(\theta '-\theta )\}\psi (\theta ')=z_{i}\psi (\theta )}$$ Note the expansion $${\displaystyle \exp\{\beta J\cos(\theta -\theta ')\}=\sum _{n=-\infty }^{\infty }I_{n}(\beta J)e^{in(\theta -\theta ')}=\sum _{n=-\infty }^{\infty }\omega _{n}\psi _{n}^{*}(\theta ')\psi _{n}(\theta )}$$

This transfer matrix approach is also required when using free boundary conditions, but with an applied field ${\displaystyle h\neq 0}$. If the applied field ${\displaystyle h}$ is small enough that it can be treated as a perturbation to the system in zero-field, then the magnetic susceptibility ${\displaystyle \chi \equiv \partial M/\partial h}$ can be estimated. This is done by using the eigenstates computed by the transfer matrix approach and computing the energy shift with second-order perturbation theory, then comparing with the free-energy expansion ${\displaystyle F=F_{0}-{\frac {1}{2}}\chi h^{2}}$. One finds $${\displaystyle \chi (h\to 0)={\frac {C}{T}}{\frac {1+\mu }{1-\mu }}}$$ where ${\displaystyle C}$ is the Curie constant (a value typically associated with the susceptibility in magnetic materials). This expression is also true for the one-dimensional Ising model, with the replacement ${\displaystyle \mu =\tanh K}$.

Two dimensions

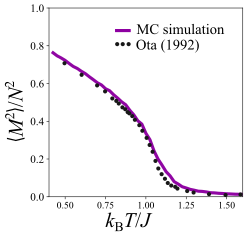
The two-dimensional XY model with nearest-neighbor interactions is an example of a two-dimensional system with continuous symmetry that does not have long-range order as required by the Mermin–Wagner theorem. Likewise, there is not a conventional phase transition present that would be associated with symmetry breaking. However, as will be discussed later, the system does show signs of a transition from a disordered high-temperature state to a quasi-ordered state below some critical temperature, called the Kosterlitz-Thouless transition. In the case of a discrete lattice of spins, the two-dimensional XY model can be evaluated using the transfer matrix approach, reducing the model to an eigenvalue problem and utilizing the largest eigenvalue from the transfer matrix. Though the exact solution is intractable, it is possible to use certain approximations to get estimates for the critical temperature ${\displaystyle T_{c}}$ which occurs at low temperatures. For example, Mattis (1984) used an approximation to this model to estimate a critical temperature of the system as $${\displaystyle (2k_{\rm {B}}T_{c}/J)\ln(2k_{\rm {B}}T_{c}/J)=1}$$ $${\displaystyle k_{\rm {B}}T_{c}/J\approx 0.8816}$$ The 2D XY model has also been studied in great detail using Monte Carlo simulations, for example with the Metropolis algorithm. These can be used to compute thermodynamic quantities like the system energy, specific heat, magnetization, etc., over a range of temperatures and time-scales. In the Monte Carlo simulation, each spin is associated to a continuously-varying angle ${\displaystyle \theta _{i}}$ (often, it can be discretized into finitely-many angles, like in the related Potts model, for ease of computation. However, this is not a requirement.) At each time step the Metropolis algorithm chooses one spin at random and rotates its angle by some random increment ${\displaystyle \Delta \theta _{i}\in (-\Delta ,\Delta )}$. This change in angle causes a change in the energy ${\displaystyle \Delta E_{i}}$ of the system, which can be positive or negative. If negative, the algorithm accepts the change in angle; if positive, the configuration is accepted with probability ${\displaystyle e^{-\beta \Delta E_{i}}}$, the Boltzmann factor for the energy change. The Monte Carlo method has been used to verify, with various methods, the critical temperature of the system, and is estimated to be ${\displaystyle k_{\rm {B}}T_{c}/J=0.8935(1)}$. The Monte Carlo method can also compute average values that are used to compute thermodynamic quantities like magnetization, spin-spin correlation, correlation lengths, and specific heat. These are important ways to characterize the behavior of the system near the critical temperature. The magnetization and squared magnetization, for example, can be computed as

$${\displaystyle {\frac {\langle M\rangle }{N}}={\frac {1}{N}}|\langle \mathbf {s} \rangle |={\frac {1}{N}}\left|\left\langle \left(\sum _{i=1}^{N}\cos \theta _{i},\sum _{i=1}^{N}\sin \theta _{i}\right)\right\rangle \right|}$$ $${\displaystyle {\frac {\langle M^{2}\rangle }{N^{2}}}={\frac {1}{N^{2}}}\left\langle s_{x}^{2}+s_{y}^{2}\right\rangle ={\frac {1}{N^{2}}}\left\langle \left(\sum _{i=1}^{N}\cos \theta _{i}\right)^{2}+\left(\sum _{i=1}^{N}\sin \theta _{i}\right)^{2}\right\rangle }$$ where ${\displaystyle N=L\times L}$ are the number of spins. The mean magnetization characterizes the magnitude of the net magnetic moment of the system; in many magnetic systems this is zero above a critical temperature and becomes non-zero spontaneously at low temperatures. Similarly the mean-squared magnetization characterizes the average of the square of net components of the spins across the lattice. Either of these are commonly used to characterize the order parameter of a system. Rigorous analysis of the XY model shows the magnetization in the thermodynamic limit is zero, and that the square magnetization approximately follows ${\displaystyle \langle M^{2}\rangle \approx N^{-T/4\pi }}$, which vanishes in the thermodynamic limit. Indeed, at high temperatures this quantity approaches zero since the components of the spins will tend to be randomized and thus sum to zero. However at low temperatures for a finite system, the mean-square magnetization increases, suggesting there are regions of the spin space that are aligned to contribute to a non-zero contribution. The magnetization shown (for a 25x25 lattice) is one example of this, that appears to suggest a phase transition, while no such transition exists in the thermodynamic limit.

Furthermore, using statistical mechanics one can relate thermodynamic averages to quantities like specific heat by calculating $${\displaystyle c/k_{\rm {B}}={\frac {\langle E^{2}\rangle -\langle E\rangle ^{2}}{N(k_{\rm {B}}T)^{2}}}}$$ The specific heat is shown at low temperatures near the critical temperature ${\displaystyle k_{\rm {B}}T_{c}/J\approx 0.88}$. There is no feature in the specific heat consistent with critical behavior (like a divergence) at this predicted temperature. Indeed, estimating the critical temperature comes from other methods, like from the helicity modulus, or the temperature dependence of the divergence of susceptibility. However, there is a feature in the specific heat in the form of a peak at ${\displaystyle k_{\rm {B}}T/J\approx 1.043(4)\approx 1.167(1)T_{c}}$. This peak position and height have been shown not to depend on system size, for lattices of linear size greater than 256; indeed, the specific heat anomaly remains rounded and finite for increasing lattice size, with no divergent peak.

The nature of the critical transitions and vortex formation can be elucidated by considering a continuous version of the XY model. Here, the discrete spins ${\displaystyle \theta _{n}}$ are replaced by a field ${\displaystyle \theta ({\textbf {x}})}$ representing the spin's angle at any point in space. In this case the angle of the spins ${\displaystyle \theta ({\textbf {x}})}$ must vary smoothly over changes in position. Expanding the original cosine as a Taylor series, the Hamiltonian can be expressed in the continuum approximation as $${\displaystyle E=\int {\frac {J}{2}}(\nabla \theta )^{2}\,d^{2}\mathbf {x} }$$

The continuous version of the XY model is often used to model systems that possess order parameters with the same kinds of symmetry, e.g. superfluid helium, hexatic liquid crystals. This is what makes them peculiar from other phase transitions which are always accompanied with a symmetry breaking. Topological defects in the XY model lead to a vortex-unbinding transition from the low-temperature phase to the high-temperature disordered phase. Indeed, the fact that at high temperature correlations decay exponentially fast, while at low temperatures decay with power law, even though in both regimes M(β) = 0, is called Kosterlitz–Thouless transition. Kosterlitz and Thouless provided a simple argument of why this would be the case: this considers the ground state consisting of all spins in the same orientation, with the addition then of a single vortex. The presence of these contributes an entropy of roughly ${\displaystyle \Delta S=k_{\rm {B}}\ln(L^{2}/a^{2})}$, where ${\displaystyle a}$ is an effective length scale (for example, the lattice size for a discrete lattice) Meanwhile, the energy of the system increases due to the vortex, by an amount ${\displaystyle \Delta E=\pi J\ln(L/a)}$. Putting these together, the free energy of a system would change due to the spontaneous formation of a vortex by an amount $${\displaystyle \Delta F=\Delta E-T\Delta S=(\pi J-2k_{\rm {B}}T)\ln(L/a)}$$ In the thermodynamic limit, the system does not favor the formation of vortices at low temperatures, but does favor them at high temperatures, above the critical temperature ${\displaystyle T_{c}=\pi J/2k_{\rm {B}}}$. This indicates that at low temperatures, any vortices that arise will want to annihilate with antivortices to lower the system energy. Indeed, this will be the case qualitatively if one watches 'snapshots' of the spin system at low temperatures, where vortices and antivortices gradually come together to annihilate. Thus, the low-temperature state will consist of bound vortex-antivortex pairs. Meanwhile at high temperatures, there will be a collection of unbound vortices and antivortices that are free to move about the plane.

To visualize the Ising model, one can use an arrow pointing up or down, or represented as a point colored black/white to indicate its state. To visualize the XY spin system, the spins can be represented as an arrow pointing in some direction, or as being represented as a point with some color. Here it is necessary to represent the spin with a spectrum of colors due to each of the possible continuous variables. This can be done using, for example, a continuous and periodic red-green-blue spectrum. As shown on the figure, cyan corresponds to a zero angle (pointing to the right), whereas red corresponds to a 180 degree angle (pointing to the left). One can then study snapshots of the spin configurations at different temperatures to elucidate what happens above and below the critical temperature of the XY model. At high temperatures, the spins will not have a preferred orientation and there will be unpredictable variation of angles between neighboring spins, as there will be no preferred energetically favorable configuration. In this case, the color map will look highly pixellated. Meanwhile at low temperatures, one possible ground-state configuration has all spins pointed in the same orientation (same angle); these would correspond to regions (domains) of the color map where all spins have roughly the same color.

To identify vortices (or antivortices) present as a result of the Kosterlitz–Thouless transition, one can determine the signed change in angle by traversing a circle of lattice points counterclockwise. If the total change in angle is zero, this corresponds to no vortex being present; whereas a total change in angle of ${\displaystyle \pm 2\pi }$ corresponds to a vortex (or antivortex). These vortexes are topologically non-trivial objects that come in vortex-antivortex pairs, which can separate or pair-annihilate. In the colormap, these defects can be identified in regions where there is a large color gradient where all colors of the spectrum meet around a point. Qualitatively, these defects can look like inward- or outward-pointing sources of flow, or whirlpools of spins that collectively clockwise or counterclockwise, or hyperbolic-looking features with some spins pointing toward and some spins pointing away from the defect. As the configuration is studied at long time scales and at low temperatures, it is observed that many of these vortex-antivortex pairs get closer together and eventually pair-annihilate. It is only at high temperatures that these vortices and antivortices are liberated and unbind from one another.

In the continuous XY model, the high-temperature spontaneous magnetization vanishes: $${\displaystyle M(\beta ):=|\langle \mathbf {s} _{i}\rangle |=0}$$ Besides, cluster expansion shows that the spin correlations cluster exponentially fast: for instance $${\displaystyle |\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\leq C(\beta )e^{-c(\beta )|i-j|}}$$ At low temperatures, i.e. β ≫ 1, the spontaneous magnetization remains zero (see the Mermin–Wagner theorem), $${\displaystyle M(\beta ):=|\langle \mathbf {s} _{i}\rangle |=0}$$ but the decay of the correlations is only power law: Fröhlich and Spencer found the lower bound

${\displaystyle |\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\geq {\frac {C(\beta )}{1+|i-j|^{\eta (\beta )}}}}$

while McBryan and Spencer found the upper bound, for any ${\displaystyle \epsilon >0}$

${\displaystyle |\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\leq {\frac {C(\beta ,\epsilon )}{1+|i-j|^{\eta (\beta ,\epsilon )}}}}$

Three and higher dimensions

Independently of the range of the interaction, at low enough temperature the magnetization is positive.

• At high temperature, the spontaneous magnetization vanishes: ${\displaystyle M(\beta ):=|\langle \mathbf {s} _{i}\rangle |=0}$. Besides, cluster expansion shows that the spin correlations cluster exponentially fast: for instance ${\displaystyle |\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\leq C(\beta )e^{-c(\beta )|i-j|}}$.
• At low temperature, infrared bound shows that the spontaneous magnetization is strictly positive: ${\displaystyle M(\beta ):=|\langle \mathbf {s} _{i}\rangle |>0}$. Besides, there exists a 1-parameter family of extremal states, ${\displaystyle \langle \;\cdot \;\rangle ^{\theta }}$, such that ${\displaystyle \langle \mathbf {s} _{i}\rangle ^{\theta }=M(\beta )(\cos \theta ,\sin \theta )}$ but, conjecturally, in each of these extremal states the truncated correlations decay algebraically.

Phase transition

As mentioned above in one dimension the XY model does not have a phase transition, while in two dimensions it has the Berezinski-Kosterlitz-Thouless transition between the phases with exponentially and powerlaw decaying correlation functions.

In three and higher dimensions the XY model has a ferromagnet-paramagnet phase transition. At low temperatures the spontaneous magnetization is nonzero: this is the ferromagnetic phase. As the temperature is increased, spontaneous magnetization gradually decreases and vanishes at a critical temperature. It remains zero at all higher temperatures: this is the paramagnetic phase.

In four and higher dimensions the phase transition has mean field theory critical exponents (with logarithmic corrections in four dimensions).

Three dimensional case: the critical exponents

The three dimensional case is interesting because the critical exponents at the phase transition are nontrivial. Many three-dimensional physical systems belong to the same universality class as the three dimensional XY model and share the same critical exponents, most notably easy-plane magnets and liquid Helium-4. The values of these critical exponents are measured by experiments, Monte Carlo simulations, and can also be computed by theoretical methods of quantum field theory, such as the renormalization group and the conformal bootstrap. Renormalization group methods are applicable because the critical point of the XY model is believed to be described by a renormalization group fixed point. Conformal bootstrap methods are applicable because it is also believed to be a unitary three dimensional conformal field theory.

Most important critical exponents of the three dimensional XY model are ${\displaystyle \alpha ,\beta ,\gamma ,\delta ,\nu ,\eta }$. All of them can be expressed via just two numbers: the scaling dimensions ${\displaystyle \Delta _{\phi }}$ and ${\displaystyle \Delta _{s}}$ of the complex order parameter field ${\displaystyle \phi }$ and of the leading singlet operator ${\displaystyle s}$ (same as${\displaystyle |\phi |^{2}}$ in the Ginzburg–Landau description). Another important field is ${\displaystyle s'}$(same as ${\displaystyle |\phi |^{4}}$), whose dimension ${\displaystyle \Delta _{s'}}$ determines the correction-to-scaling exponent ${\displaystyle \omega }$. According to a conformal bootstrap computation, these three dimensions are given by:

${\displaystyle \Delta _{\phi }}$	0.519088(22)
${\displaystyle \Delta _{s}}$	1.51136(22)
${\displaystyle \Delta _{s'}}$	3.794(8)

This gives the following values of the critical exponents:

	general expression (${\displaystyle d=3}$)	numerical value
α	${\displaystyle 2-d/(d-\Delta _{s})}$	-0.01526(30)
β	${\displaystyle \Delta _{\phi }/(d-\Delta _{s})}$	0.34869(7)
γ	${\displaystyle (d-2\Delta _{\phi })/(d-\Delta _{s})}$	1.3179(2)
δ	${\displaystyle (d-\Delta _{\phi })/\Delta _{\phi }}$	4.77937(25)
η	${\displaystyle 2\Delta _{\phi }-d+2}$	0.038176(44)
ν	${\displaystyle 1/(d-\Delta _{s})}$	0.67175(10)
ω	${\displaystyle \Delta _{s'}-d}$	0.794(8)

Monte Carlo methods give compatible determinations: ${\displaystyle \eta =0.03810(8),\nu =0.67169(7),\omega =0.789(4)}$.

See also

• Classical Heisenberg model
• Coulomb gas
• Goldstone boson
• Ising model
• Potts model
• n-vector model
• Kosterlitz–Thouless transition
• Topological defect
• Superfluid film
• Sigma model
• Sine-Gordon model

Notes

1. Stanley, H.E. (1968). "Dependence of Critical Properties on Dimensionality of Spins". Physical Review Letters. 20 (12): 589–592. Bibcode:1968PhRvL..20..589S. doi:10.1103/PhysRevLett.20.589.
2. Chaikin, P.M.; Lubensky, T.C. (2000). Principles of Condensed Matter Physics. Cambridge University Press. ISBN 978-0521794503.
3. Ginibre, J. (1970). "General formulation of Griffiths' inequalities". Communications in Mathematical Physics. 16 (4): 310–328. Bibcode:1970CMaPh..16..310G. doi:10.1007/BF01646537. S2CID 120649586.
4. Aizenman, M.; Simon, B. (1980). "A comparison of plane rotor and Ising models". Physics Letters A. 76 (3–4): 281–282. Bibcode:1980PhLA...76..281A. doi:10.1016/0375-9601(80)90493-4.
5. Badalian, D. (1996). "On the thermodynamics of classical spins with isotrop Heisenberg interaction in one-dimensional quasi-periodic structures". Physica B. 226 (4): 385–390. Bibcode:1996PhyB..226..385B. doi:10.1016/0921-4526(96)00283-9.
6. Mattis, D.C. (1984). "Transfer matrix in plane-rotator model". Physics Letters A. 104 A (6–7): 357–360. Bibcode:1984PhLA..104..357M. doi:10.1016/0375-9601(84)90816-8.
7. Mattis, D. C. (1985). The Theory of Magnetism II. Springer Series in Solid-State Physics. ISBN 978-3-642-82405-0.
8. Ota, S.; Ota, S.B.; Fahnle, M (1992). "Microcanonical Monte Carlo simulations for the two-dimensional XY model". Journal of Physics: Condensed Matter. 4 (24): 5411. Bibcode:1992JPCM....4.5411O. doi:10.1088/0953-8984/4/24/011. S2CID 250920391.
9. Mattis, Daniel (1984). "Transfer matrix in plane-rotator model". Physics Letters A. 104 (6–7): 357–360.
10. Hsieh, Y.-D.; Kao, Y.-J.; Sandvik, A.W. (2013). "Finite-size scaling method for the Berezinskii-Kosterlitz-Thouless transition". Journal of Statistical Mechanics: Theory and Experiment. 2013 (9): P09001. arXiv:1302.2900. Bibcode:2013JSMTE..09..001H. doi:10.1088/1742-5468/2013/09/P09001. S2CID 118609225.
11. Nguyen, P.H.; Boninsegni, M. (2021). "Superfluid Transition and Specific Heat of the 2D x-y Model: Monte Carlo Simulation". Applied Sciences. 11 (11): 4931. arXiv:2105.14112. doi:10.3390/app11114931.
12. Tobochnik, J.; Chester, G.V. (1979). "Monte Carlo study of the planar spin model". Physical Review B. 20 (9): 3761–3769. Bibcode:1979PhRvB..20.3761T. doi:10.1103/PhysRevB.20.3761.
13. Binder, K. (2013). Applications of the Monte Carlo Method in Statistical Physics. Springer Science & Business Media. ISBN 978-3-642-51703-7.
14. Fröhlich, J.; Spencer, T. (1981). "The Kosterlitz–Thouless transition in two-dimensional abelian spin systems and the Coulomb gas". Communications in Mathematical Physics. 81 (4): 527–602. Bibcode:1981CMaPh..81..527F. doi:10.1007/bf01208273. S2CID 73555642.
15. Chester, Shai M.; Landry, Walter; Liu, Junyu; Poland, David; Simmons-Duffin, David; Su, Ning; Vichi, Alessandro (2020). "Carving out OPE space and precise O(2) model critical exponents". Journal of High Energy Physics. 2020 (6): 142. arXiv:1912.03324. Bibcode:2020JHEP...06..142C. doi:10.1007/JHEP06(2020)142. ISSN 1029-8479. S2CID 208910721.
16. Hasenbusch, Martin (2019-12-26). "Monte Carlo study of an improved clock model in three dimensions". Physical Review B. 100 (22): 224517. arXiv:1910.05916. Bibcode:2019PhRvB.100v4517H. doi:10.1103/PhysRevB.100.224517. ISSN 2469-9950. S2CID 204509042.

References

• Evgeny Demidov, Vortices in the XY model (2004)

Further reading

• H. E. Stanley, Introduction to Phase Transitions and Critical Phenomena, (Oxford University Press, Oxford and New York 1971);
• H. Kleinert, Gauge Fields in Condensed Matter, Vol. I, " SUPERFLOW AND VORTEX LINES", pp. 1–742, Vol. II, "STRESSES AND DEFECTS", pp. 743–1456, World Scientific (Singapore, 1989); Paperback ISBN 9971-5-0210-0 (also available online: Vol. I and Vol. II)

External links

• real-time XY model WebGL simulation
• Interactive Monte Carlo simulation of the Ising, XY and Heisenberg models with 3D graphics (requires WebGL compatible browser)

• Lattice models