Browse history interactively← Previous editContent deleted Content addedVisualWikitextInline

Revision as of 18:45, 18 August 2007 edit137.99.17.121 (talk) →Convenience: emphasis --> emphasize← Previous edit		Latest revision as of 19:39, 24 December 2024 edit undoJacobolus (talk | contribs)Extended confirmed users35,521 edits Undid revision 1265035192 by 2600:1700:4268:6030:8851:28F4:F004:DCF8 (talk) – the identity you added is not common or particularly interesting/noteworthy in context. we don't need to mention every possible identity which could be extracted from the figure in this already overlong caption.Tag: Undo
Line 1:		Line 1:
			{{Short description|none}}
	{{Citations missing|date=July 2007}}
			{{Trigonometry}}
	In ], '''trigonometric identities''' are equalities that involve ]s that are true for all values of the occurring variables. These ] are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the ] of non-trigonometric functions: a common trick involves first using the ], and then simplifying the resulting integral with a trigonometric identity.
			In ], '''trigonometric identities''' are ] that involve ] and are true for every value of the occurring ] for which both sides of the equality are defined. Geometrically, these are ] involving certain functions of one or more ]s. They are distinct from ], which are identities potentially involving angles but also involving side lengths or other lengths of a ].
			These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the ] of non-trigonometric functions: a common technique involves first using the ], and then simplifying the resulting integral with a trigonometric identity.
	]
	]]]
			== Pythagorean identities ==
	==Notation==
			{{Main|Pythagorean trigonometric identity}}
			]
			The basic relationship between the ] is given by the Pythagorean identity:
	To avoid the confusion caused by the ambiguity of sin<sup>&minus;1</sup>(''x''), the reciprocals and inverses of trigonometric functions are often displayed as in this table. In representing the cosecant function, the longer form 'cosec' is sometimes used in place of 'csc'.
			<math display="block">\sin^2\theta + \cos^2\theta = 1,</math>
	{|class="wikitable" style="background-color:#FFFFFF;"
	!colspan="2"| Function
			where <math>\sin^2 \theta</math> means <math>(\sin \theta)^2</math> and <math>\cos^2 \theta</math> means <math>(\cos \theta)^2.</math>
	!colspan="2"| ]
	!colspan="2"| ]
			This can be viewed as a version of the ], and follows from the equation <math>x^2 + y^2 = 1</math> for the ]. This equation can be solved for either the sine or the cosine:
	!colspan="2"| Inverse reciprocal
			<math display=block>\begin{align}
			\sin\theta &= \pm \sqrt{1 - \cos^2\theta}, \\
			\cos\theta &= \pm \sqrt{1 - \sin^2\theta}.
			\end{align}</math>
			where the sign depends on the ] of <math>\theta.</math>
			Dividing this identity by <math>\sin^2 \theta</math>, <math>\cos^2 \theta</math>, or both yields the following identities:
			<math display=block>\begin{align}
			&1 + \cot^2\theta = \csc^2\theta \\
			&1 + \tan^2\theta = \sec^2\theta \\
			&\sec^2\theta + \csc^2\theta = \sec^2\theta\csc^2\theta
			\end{align}</math>
			Using these identities, it is possible to express any trigonometric function in terms of any other (] a plus or minus sign):
			{| class="wikitable" style="text-align:center"
			|+ Each trigonometric function in terms of each of the other five.<ref name="AS4345">{{AS ref|4, eqn 4.3.45|73}}</ref>
			! scope=row | in terms of
			! scope="col"|<math>\sin \theta</math>
			! scope="col" |<math>\csc \theta</math>
			! scope="col"|<math>\cos \theta</math>
			! scope="col" |<math>\sec \theta</math>
			! scope="col"|<math>\tan \theta</math>
			! scope="col"|<math>\cot \theta</math>
	|-		|-
			! scope=row | <math>\sin \theta =</math>
	| sine
			| <math>\sin \theta</math>
	| sin
			| <math>\frac{1}{\csc \theta}</math>
	| arcsine
			| <math>\pm\sqrt{1 - \cos^2 \theta}</math>
	| arcsin
			| <math>\pm\frac{\sqrt{\sec^2 \theta - 1}}{\sec \theta}</math>
	| cosecant
			| <math>\pm\frac{\tan \theta}{\sqrt{1 + \tan^2 \theta}}</math>
	| csc
			| <math>\pm\frac{1}{\sqrt{1 + \cot^2 \theta}}</math>
	| arccosecant
	| arccsc
	|-		|-
			! scope=row | <math>\csc \theta =</math>
	| cosine
			| <math>\frac{1}{\sin \theta}</math>
	| cos
			| <math>\csc \theta</math>
	| arccosine
			| <math>\pm\frac{1}{\sqrt{1 - \cos^2 \theta}}</math>
	| arccos
			| <math>\pm\frac{\sec \theta}{\sqrt{\sec^2 \theta - 1}}</math>
	| secant
			| <math>\pm\frac{\sqrt{1 + \tan^2 \theta}}{\tan \theta}</math>
	| sec
			| <math>\pm\sqrt{1 + \cot^2 \theta}</math>
	| arcsecant
	| arcsec
	|-		|-
			! scope=row | <math>\cos \theta =</math>
	| tangent
			| <math>\pm\sqrt{1 - \sin^2\theta}</math>
	| tan
			| <math>\pm\frac{\sqrt{\csc^2 \theta - 1}}{\csc \theta}</math>
	| arctangent
			| <math>\cos \theta</math>
	| arctan
			| <math>\frac{1}{\sec \theta}</math>
	| cotangent
			| <math>\pm\frac{1}{\sqrt{1 + \tan^2 \theta}}</math>
	| cot
			| <math>\pm\frac{\cot \theta}{\sqrt{1 + \cot^2 \theta}}</math>
	| arccotangent
	| arccot
	|}
	Different angular measures can be appropriate in different situations. This table shows some of the more common systems.
	Radians is the default angular measure and is the one you use if you use the exponential definitions. All angular measures are unitless.
	{|class="wikitable" style="background-color: #FFFFFF; text-align: center;"
	|-		|-
			! scope=row | <math>\sec \theta =</math>
	! ]s
			| <math>\pm\frac{1}{\sqrt{1 - \sin^2 \theta}}</math>
	| 30
			| <math>\pm\frac{\csc \theta}{\sqrt{\csc^2 \theta - 1}}</math>
	| 45
			| <math>\frac{1}{\cos \theta}</math>
	| 60
			| <math>\sec \theta</math>
	| 90
			| <math>\pm\sqrt{1 + \tan^2 \theta}</math>
	| 120
			| <math>\pm\frac{\sqrt{1 + \cot^2 \theta}}{\cot \theta}</math>
	| 180
	| 270
	! 360
	|-		|-
			! scope=row | <math>\tan \theta =</math>
	! ]s
	| <math>\pi/6</math>		| <math>\pm\frac{\sin \theta}{\sqrt{1 - \sin^2 \theta}}</math>
	| <math>\pi/4</math>		| <math>\pm\frac{1}{\sqrt{\csc^2 \theta - 1}}</math>
	| <math>\pi/3</math>		| <math>\pm\frac{\sqrt{1 - \cos^2 \theta}}{\cos \theta}</math>
	| <math>\pi/2</math>		| <math>\pm\sqrt{\sec^2 \theta - 1}</math>
	| <math>2\pi/3</math>		| <math>\tan \theta</math>
	| <math>\pi</math>		| <math>\frac{1}{\cot \theta}</math>
	| <math>3\pi/2</math>
	! <math>2\pi</math>
	|-		|-
			! scope=row | <math>\cot \theta =</math>
	! ]s
			| <math>\pm\frac{\sqrt{1 - \sin^2 \theta}}{\sin \theta}</math>
	| 33 ⅓
			| <math>\pm\sqrt{\csc^2 \theta - 1}</math>
	| 50
			| <math>\pm\frac{\cos \theta}{\sqrt{1 - \cos^2 \theta}}</math>
	| 66 ⅔
			| <math>\pm\frac{1}{\sqrt{\sec^2 \theta - 1}}</math>
	| 100
			| <math>\frac{1}{\tan \theta}</math>
	| 133 ⅓
			| <math>\cot \theta</math>
	| 200
	| 300
	! 400
	|}		|}
	==Basic relationships==
			== Reflections, shifts, and periodicity ==
	{|class="wikitable" style="background-color:#FFFFFF"
			By examining the unit circle, one can establish the following properties of the trigonometric functions.
	! ]
	|<math>\sin^2 \theta + \cos^2 \theta = 1\,</math><ref name="mathworld_trigonometry">{{MathWorld|title=Trigonometry|urlname=Trigonometry}}</ref>
			=== Reflections ===
			]
			When the direction of a Euclidean vector is represented by an angle <math>\theta,</math> this is the angle determined by the free vector (starting at the origin) and the positive <math>x</math>-unit vector. The same concept may also be applied to lines in a Euclidean space, where the angle is that determined by a parallel to the given line through the origin and the positive <math>x</math>-axis. If a line (vector) with direction <math>\theta</math> is reflected about a line with direction <math>\alpha,</math> then the direction angle <math>\theta^{\prime}</math> of this reflected line (vector) has the value
			<math display="block">\theta^{\prime} = 2 \alpha - \theta.</math>
			The values of the trigonometric functions of these angles <math>\theta,\;\theta^{\prime}</math> for specific angles <math>\alpha</math> satisfy simple identities: either they are equal, or have opposite signs, or employ the complementary trigonometric function. These are also known as {{em|reduction formulae}}.<ref>{{harvnb|Selby|1970|loc=p. 188}}</ref>
			{|class="wikitable"
			! <math>\theta</math> reflected in <math>\alpha = 0</math><ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.13–15</ref><br /><span style="font-weight:normal">] identities</span>
			! <math>\theta</math> reflected in <math>\alpha = \frac{\pi}{4}</math>
			! <math>\theta</math> reflected in <math>\alpha = \frac{\pi}{2}</math>
			! <math>\theta</math> reflected in <math>\alpha = \frac{3\pi}{4}</math>
			! <math>\theta</math> reflected in <math>\alpha = \pi</math><br /><span style="font-weight:normal">compare to <math>\alpha = 0</math></span>
	|-		|-
			|<math>\sin(-\theta) = -\sin \theta</math>
	! ]
	|<math>\tan \theta = \frac{\sin \theta}{\cos \theta}</math><ref name="mathworld_trigonometry"/>		|<math>\sin\left(\tfrac{\pi}{2} - \theta\right) =\cos \theta</math>
			|<math>\sin(\pi - \theta) = +\sin \theta</math>
	|}
			|<math>\sin\left(\tfrac{3\pi}{2} - \theta\right) =-\cos \theta</math>
	From the two identities above, the following table can be extrapolated.
			|<math>\sin(2\pi - \theta) = -\sin(\theta) = \sin(-\theta)</math>
	{| class="wikitable" style="background-color:#FFFFFF;text-align:center"
	|+ Each trigonometric function in terms of the other five.
	! Function
	! sin
	! cos
	! tan
	! csc
	! sec
	! cot
	|-		|-
	! <math>\sin \theta =</math>		|<math>\cos(-\theta) =+ \cos \theta</math>
	| <math> \sin \theta\ </math>		|<math>\cos\left(\tfrac{\pi}{2} - \theta\right) = \sin \theta</math>
	| <math> \sqrt{1 - \cos^2\theta} </math>		|<math>\cos(\pi - \theta) = -\cos \theta</math>
	| <math> \frac{\tan\theta}{\sqrt{1 + \tan^2\theta}} </math>		|<math>\cos\left(\tfrac{3\pi}{2} - \theta\right) = -\sin \theta</math>
	| <math> \frac{1}{\csc \theta} </math>		|<math>\cos(2\pi - \theta) = +\cos(\theta) = \cos(-\theta)</math>
	| <math> \frac{\sqrt{\sec^2 \theta - 1}}{\sec \theta} </math>
	| <math> \frac{1}{\sqrt{1+\cot^2\theta}} </math>
	|-		|-
	! <math>\cos \theta =</math>		|<math>\tan(-\theta) = -\tan \theta</math>
	| <math> \sqrt{1 - \sin^2\theta} </math>		|<math>\tan\left(\tfrac{\pi}{2} - \theta\right) = \cot \theta</math>
	| <math> \cos \theta\ </math>		|<math>\tan(\pi - \theta) = -\tan \theta</math>
	| <math> \frac{1}{\sqrt{1 + \tan^2 \theta}} </math>		|<math>\tan\left(\tfrac{3\pi}{2} - \theta\right) = +\cot \theta</math>
	| <math> \frac{\sqrt{\csc^2\theta - 1}}{\csc \theta} </math>		|<math>\tan(2\pi - \theta) = -\tan(\theta) = \tan(-\theta)</math>
	| <math> \frac{1}{\sec \theta} </math>
	| <math> \frac{\cot \theta}{\sqrt{1 + \cot^2 \theta}} </math>
	|-		|-
	! <math>\tan \theta =</math>		|<math>\csc(-\theta) = -\csc \theta</math>
	| <math> \frac{\sin\theta}{\sqrt{1 - \sin^2\theta}} </math>		|<math>\csc\left(\tfrac{\pi}{2} - \theta\right) = \sec \theta</math>
	| <math> \frac{\sqrt{1 - \cos^2\theta}}{\cos \theta} </math>		|<math>\csc(\pi - \theta) =+ \csc \theta</math>
	| <math> \tan \theta\ </math>		|<math>\csc\left(\tfrac{3\pi}{2} - \theta\right) = -\sec \theta</math>
	| <math> \frac{1}{\sqrt{\csc^2\theta - 1}} </math>		|<math>\csc(2\pi - \theta) = -\csc(\theta) = \csc(-\theta)</math>
	| <math> \sqrt{\sec^2\theta - 1} </math>
	| <math> \frac{1}{\cot \theta} </math>
	|-		|-
	! <math>\csc \theta =</math>		|<math>\sec(-\theta) = +\sec \theta</math>
	| <math> {1 \over \sin \theta} </math>		|<math>\sec\left(\tfrac{\pi}{2} - \theta\right) = \csc \theta</math>
	| <math> {1 \over \sqrt{1 - \cos^2 \theta}} </math>		|<math>\sec(\pi - \theta) = -\sec \theta</math>
	| <math> {\sqrt{1 + \tan^2\theta} \over \tan \theta} </math>		|<math>\sec\left(\tfrac{3\pi}{2} - \theta\right) = -\csc \theta</math>
	| <math> \csc \theta\ </math>		|<math>\sec(2\pi - \theta) = +\sec(\theta) = \sec(-\theta)</math>
	| <math> {\sec \theta \over \sqrt{\sec^2\theta - 1}} </math>
	| <math> \sqrt{1 + \cot^2 \theta} </math>
	|-		|-
	! <math>\sec \theta =</math>		|<math>\cot(-\theta) = -\cot \theta</math>
	| <math> {1 \over \sqrt{1 - \sin^2\theta}} </math>		|<math>\cot\left(\tfrac{\pi}{2} - \theta\right) = \tan \theta</math>
	| <math> {1 \over \cos \theta} </math>		|<math>\cot(\pi - \theta) = -\cot \theta</math>
	| <math> \sqrt{1 + \tan^2\theta} </math>		|<math>\cot\left(\tfrac{3\pi}{2} - \theta\right) = +\tan \theta</math>
	| <math> {\csc\theta \over \sqrt{\csc^2\theta - 1}} </math>		|<math>\cot(2\pi - \theta) = -\cot(\theta) = \cot(-\theta)</math>
	| <math>\sec\theta\ </math>
	| <math> {\sqrt{1 + \cot^2\theta} \over \cot \theta} </math>
	|-
	! <math>\cot \theta =</math>
	| <math> {\sqrt{1 - \sin^2\theta} \over \sin \theta} </math>
	| <math> {\cos \theta \over \sqrt{1 - \cos^2\theta}} </math>
	| <math> {1 \over \tan\theta} </math>
	| <math> \sqrt{\csc^2\theta - 1} </math>
	| <math> {1 \over \sqrt{\sec^2\theta - 1}} </math>
	| <math> \cot\theta\ </math>
	|}		|}
			=== Shifts and periodicity ===
	==Historic shorthands==
			]
	Rarely used today, the ], ], ], and ] have been defined as below and used in navigation, for example the ] was used to calculate the distance between two points on a sphere.
	{|class="wikitable" style="background-color:#FFFFFF"		{|class="wikitable"
			!Shift by one quarter period
			!Shift by one half period
			!Shift by full periods<ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.7–9</ref>
			!Period
	|-		|-
			|<math>\sin(\theta \pm \tfrac{\pi}{2}) = \pm\cos \theta</math>
	! Name
			|<math>\sin(\theta + \pi) = -\sin \theta</math>
	! Value
			|<math>\sin(\theta + k\cdot 2\pi) = +\sin \theta</math>
			|style="text-align: center;"|<math>2\pi</math>
	|-		|-
	| <math>\textrm{versin} \, \theta</math>		|<math>\cos(\theta \pm \tfrac{\pi}{2}) = \mp\sin \theta</math>
	| <math> 1 - \cos \theta \,</math>		|<math>\cos(\theta + \pi) = -\cos \theta</math>
			|<math>\cos(\theta + k\cdot 2\pi) = +\cos \theta</math>
			|style="text-align: center;"|<math>2\pi</math>
	|-		|-
	|<math>\textrm{coversin} \, \theta</math>		|<math>\csc(\theta \pm \tfrac{\pi}{2}) = \pm\sec \theta</math>
	|<math>1 - \sin \theta \,</math>		|<math>\csc(\theta + \pi) = -\csc \theta</math>
			|<math>\csc(\theta + k\cdot 2\pi) = +\csc \theta</math>
			|style="text-align: center;"|<math>2\pi</math>
	|-		|-
	|<math>\textrm{haversin} \, \theta</math>		|<math>\sec(\theta \pm \tfrac{\pi}{2}) = \mp\csc \theta</math>
	|<math>\tfrac{1}{2} \textrm{versin} \theta \,</math>		|<math>\sec(\theta + \pi) = -\sec \theta</math>
			|<math>\sec(\theta + k\cdot 2\pi) = +\sec \theta</math>
			|style="text-align: center;"|<math>2\pi</math>
	|-		|-
	|<math>\textrm{exsec} \, \theta \,</math>		|<math>\tan(\theta \pm \tfrac{\pi}{4}) = \tfrac{\tan \theta \pm 1}{1\mp \tan \theta}</math>
	|<math> \sec \theta - 1 \,</math>		|<math>\tan(\theta + \tfrac{\pi}{2}) = -\cot \theta</math>
			|<math>\tan(\theta + k\cdot \pi) = +\tan \theta</math>
			|style="text-align: center;"|<math>\pi</math>
			|-
			|<math>\cot(\theta \pm \tfrac{\pi}{4}) = \tfrac{\cot \theta \mp 1}{1\pm \cot \theta}</math>
			|<math>\cot(\theta + \tfrac{\pi}{2}) = -\tan\theta</math>
			|<math>\cot(\theta + k\cdot \pi) = +\cot \theta</math>
			|style="text-align: center;"|<math>\pi</math>
	|}		|}
			=== Signs ===
	==Symmetry, shifts, and periodicity==
	By examining the unit circle, the following properties of the trigonometric functions can be established.
			The sign of trigonometric functions depends on quadrant of the angle. If <math>{-\pi} < \theta \leq \pi</math> and {{math|sgn}} is the ],
	===Symmetry===
	When the trigonometric functions are reflected from certain values of <math>\theta</math>, The result is often one of the other trigonometric functions. This leads to the following identities:
	{|class="wikitable" style="background-color: #FFFFFF"
	! Reflected in <math>\theta=0</math>
	! Reflected in <math>\theta= \pi/2</math>
	! Reflected in <math>\theta= \pi</math>
	|-
			<math display=block>\begin{align}
	|<math>
			\sgn(\sin \theta) = \sgn(\csc \theta) &= \begin{cases}
	\begin{align}
	\sin(0-\theta) &= -\sin \theta \\		+1 & \text{if}\ \ 0 < \theta < \pi \\
	\cos(0-\theta) &= +\cos \theta \\		-1 & \text{if}\ \ {-\pi} < \theta < 0 \\
	\tan(0-\theta) &= -\tan \theta \\		0 & \text{if}\ \ \theta \in \{0, \pi \}
			\end{cases}
	\csc(0-\theta) &= -\csc \theta \\
			\\
	\sec(0-\theta) &= +\sec \theta \\
	\cot(0-\theta) &= -\cot \theta		\sgn(\cos \theta) = \sgn(\sec \theta) &= \begin{cases}
			+1 & \text{if}\ \ {-\tfrac12\pi} < \theta < \tfrac12\pi \\
	\end{align}
			-1 & \text{if}\ \ {-\pi} < \theta < -\tfrac12\pi \ \ \text{or}\ \ \tfrac12\pi < \theta < \pi\\
	</math>
			0 & \text{if}\ \ \theta \in \bigl\{{-\tfrac12\pi}, \tfrac12\pi \bigr\}
	|<math>
	\begin{align}		\end{cases}
			\\
	\sin(\tfrac{\pi}{2} - \theta) &= +\cos \theta \\
	\cos(\tfrac{\pi}{2} - \theta) &= +\sin \theta \\		\sgn(\tan \theta) = \sgn(\cot \theta) &= \begin{cases}
	\tan(\tfrac{\pi}{2} - \theta) &= +\cot \theta \\		+1 & \text{if}\ \ {-\pi} < \theta < -\tfrac12\pi \ \ \text{or}\ \ 0 < \theta < \tfrac12\pi \\
	\csc(\tfrac{\pi}{2} - \theta) &= +\sec \theta \\		-1 & \text{if}\ \ {-\tfrac12\pi} < \theta < 0 \ \ \text{or}\ \ \tfrac12\pi < \theta < \pi \\
			0 & \text{if}\ \ \theta \in \bigl\{{-\tfrac12\pi}, 0, \tfrac12\pi, \pi \bigr\}
	\sec(\tfrac{\pi}{2} - \theta) &= +\csc \theta \\
			\end{cases}
	\cot(\tfrac{\pi}{2} - \theta) &= +\tan \theta
	\end{align}		\end{align}</math>
	</math>
	|<math>
	\begin{align}
	\sin(\pi - \theta) &= +\sin \theta \\
	\cos(\pi - \theta) &= -\cos \theta \\
	\tan(\pi - \theta) &= -\tan \theta \\
	\csc(\pi - \theta) &= +\csc \theta \\
	\sec(\pi - \theta) &= -\sec \theta \\
	\cot(\pi - \theta) &= -\cot \theta \\
	\end{align}
	</math>
	|}
	===Shifts and periodicity===
			The trigonometric functions are periodic with common period <math>2\pi,</math> so for values of {{mvar|θ}} outside the interval <math>({-\pi}, \pi],</math> they take repeating values (see {{slink|#Shifts and periodicity}} above).
	By shifting the function round by certain angles, it is often possible to find different trigonometric functions that express the result more simply. Some examples of this are given shown by shifting functions round by π/2, π and 2π radians. Because the periods of these functions are either π or 2π, there are cases where the new function is exactly the same as the old function without the shift.
			== Angle sum and difference identities ==
	{|class="wikitable" style="background-color: #FFFFFF"
			{{See also|Proofs of trigonometric identities#Angle sum identities|Small-angle approximation#Angle sum and difference}}
	!Shift by π/2
			]
	!Shift by π <br/> Period for tan and cot
	!Shift by 2π <br/> Period for sin, cos, csc and sec
	|-
	|<math>
	\begin{align}
	\sin(\theta + \tfrac{\pi}{2}) &= +\cos \theta \\
	\cos(\theta + \tfrac{\pi}{2}) &= -\sin \theta \\
	\tan(\theta + \tfrac{\pi}{2}) &= -\cot \theta \\
	\csc(\theta + \tfrac{\pi}{2}) &= +\sec \theta \\
	\sec(\theta + \tfrac{\pi}{2}) &= -\csc \theta \\
	\cot(\theta + \tfrac{\pi}{2}) &= -\tan \theta
	\end{align}
	</math>
	|<math>
	\begin{align}
	\sin(\theta + \pi) &= -\sin \theta \\
	\cos(\theta + \pi) &= -\cos \theta \\
	\tan(\theta + \pi) &= +\tan \theta \\
	\csc(\theta + \pi) &= -\csc \theta \\
	\sec(\theta + \pi) &= -\sec \theta \\
	\cot(\theta + \pi) &= +\cot \theta \\
	\end{align}
	</math>
	|<math>
	\begin{align}
	\sin(\theta + 2\pi) &= +\sin \theta \\
	\cos(\theta + 2\pi) &= +\cos \theta \\
	\tan(\theta + 2\pi) &= +\tan \theta \\
	\csc(\theta + 2\pi) &= +\csc \theta \\
	\sec(\theta + 2\pi) &= +\sec \theta \\
	\cot(\theta + 2\pi) &= +\cot \theta
	\end{align}
	</math>
	|}
			]
	==Angle sum and difference identities==
	These are also known as the ''addition and subtraction theorems'' or ''formulæ''.
	The quickest way to prove these is ].
			These are also known as the {{em|angle addition and subtraction theorems}} (or {{em|formulae}}).
	{|class="wikitable" style="background-color: #FFFFFF"
			<math display=block>\begin{align}
	!Sine
			\sin(\alpha + \beta) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \\
	|<math>\sin(\theta \pm \phi) = \sin \theta \cos \phi \pm \cos \theta \sin \phi \,</math><ref name="mathworld_addition">{{MathWorld|title=Trigonometric Addition Formulas|urlname=TrigonometricAdditionFormulas}}</ref>
			\sin(\alpha - \beta) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta \\
	|rowspan="3"| ''Note:'' From ].
			\cos(\alpha + \beta) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \\
	<math>\begin{align}x \pm y = a \pm b &\Rightarrow \ x + y = a + b \\ &\mbox{and} \ x -y = a -b \end{align}</math><br/><math>\begin{align}
			\cos(\alpha - \beta) &= \cos \alpha \cos \beta + \sin \alpha \sin \beta
	x \pm y = a \mp b &\Rightarrow \ x + y = a - b \\ &\mbox{and}\ x - y = a + b\end{align}</math>
			\end{align}</math>
			The angle difference identities for <math>\sin(\alpha - \beta)</math> and <math>\cos(\alpha - \beta)</math> can be derived from the angle sum versions by substituting <math>-\beta</math> for <math>\beta</math> and using the facts that <math>\sin(-\beta) = -\sin(\beta)</math> and <math>\cos(-\beta) = \cos(\beta)</math>. They can also be derived by using a slightly modified version of the figure for the angle sum identities, both of which are shown here.
			These identities are summarized in the first two rows of the following table, which also includes sum and difference identities for the other trigonometric functions.
			{|class="wikitable" style="background-color:var(--background-color-base)"
			! Sine
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\sin(\alpha \pm \beta)</math>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\sin \alpha \cos \beta \pm \cos \alpha \sin \beta</math><ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.16</ref><ref name="mathworld_addition">{{MathWorld|title=Trigonometric Addition Formulas|urlname=TrigonometricAdditionFormulas}}</ref>
	|-		|-
	!Cosine		! Cosine
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\cos(\alpha \pm \beta)</math>
	|<math>\cos(\theta \pm \phi) = \cos \theta \cos \phi \mp \sin \theta \sin \phi\,</math><ref name="mathworld_addition"/>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\cos \alpha \cos \beta \mp \sin \alpha \sin \beta</math><ref name="mathworld_addition" /><ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.17</ref>
	|-		|-
	!Tangent		! Tangent
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\tan(\alpha \pm \beta)</math>
	|<math>\tan(\theta \pm \phi) = \frac{\tan \theta \pm \tan \phi}{1 \mp \tan \theta \tan \phi}</math><ref name="mathworld_addition"/>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}</math><ref name="mathworld_addition" /><ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.18</ref>
			|-
			!Cosecant
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\csc(\alpha \pm \beta)</math>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\frac{\sec \alpha \sec \beta \csc \alpha \csc \beta}{\sec \alpha \csc \beta \pm \csc \alpha \sec \beta}</math><ref name=":0">{{Cite web|url=http://www.milefoot.com/math/trig/22anglesumidentities.htm|title=Angle Sum and Difference Identities|website=www.milefoot.com|access-date=2019-10-12}}</ref>
			|-
			! Secant
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\sec(\alpha \pm \beta)</math>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\frac{\sec \alpha \sec \beta \csc \alpha \csc \beta}{\csc \alpha \csc \beta \mp \sec \alpha \sec \beta}</math><ref name=":0" />
			|-
			! Cotangent
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\cot(\alpha \pm \beta)</math>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\frac{\cot \alpha \cot \beta \mp 1}{\cot \beta \pm \cot \alpha}</math><ref name="mathworld_addition" /><ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.19</ref>
			|-
			! Arcsine
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\arcsin x \pm \arcsin y</math>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\arcsin\left(x\sqrt{1-y^2} \pm y\sqrt{1-x^2\vphantom{y}}\right)</math><ref>Abramowitz and Stegun, p.&nbsp;80, 4.4.32</ref>
			|-
			! Arccosine
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\arccos x \pm \arccos y</math>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\arccos\left(xy \mp \sqrt{\left(1-x^2\right)\left(1-y^2\right)}\right)</math><ref>Abramowitz and Stegun, p.&nbsp;80, 4.4.33</ref>
			|-
			! Arctangent
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\arctan x \pm \arctan y</math>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\arctan\left(\frac{x \pm y}{1 \mp xy}\right)</math><ref>Abramowitz and Stegun, p.&nbsp;80, 4.4.34</ref>
			|-
			! Arccotangent
			| colspan="3" style='border-style: solid none solid solid; text-align: right;' |<math>\arccot x \pm \arccot y</math>
			| style='border-style: solid none solid none; text-align: center;' |<math>=</math>
			| style='border-style: solid solid solid none; text-align: left;' |<math>\arccot\left(\frac{xy \mp 1}{y \pm x}\right)</math>
	|}		|}
	=== Sines and cosines of sums of infinitely many terms ===		=== Sines and cosines of sums of infinitely many angles ===
			When the series <math display="inline">\sum_{i=1}^\infty \theta_i</math> ] then
			<math display=block>\begin{align}
	: <math> \sin\left(\sum_{i=1}^\infty \theta_i\right)
			{\sin}\biggl(\sum_{i=1}^\infty \theta_i\biggl)
	=\sum_{\mathrm{odd}\ k \ge 1} (-1)^{(k-1)/2}
			&= \sum_{\text{odd}\ k \ge 1} (-1)^\frac{k-1}{2} \!\!
	\sum_{ |A| = k }
			\sum_{\begin{smallmatrix} A \subseteq \{\,1,2,3,\dots\,\} \\
	\left(\prod_{i \in A} \sin\theta_i \prod_{i \not \in A} \cos\theta_i\right) </math>
			\left|A\right| = k\end{smallmatrix}}
			\biggl(\prod_{i \in A} \sin\theta_i \prod_{i \not \in A} \cos\theta_i\biggr) \\
			{\cos}\biggl(\sum_{i=1}^\infty \theta_i\biggr)
			&= \sum_{\text{even}\ k \ge 0} (-1)^\frac{k}{2} \,
			\sum_{\begin{smallmatrix} A \subseteq \{\,1,2,3,\dots\,\} \\ \left|A\right| = k\end{smallmatrix}}
			\biggl(\prod_{i \in A} \sin\theta_i \prod_{i \not \in A} \cos\theta_i\biggr) .
			\end{align}</math>
			Because the series <math display="inline">\sum_{i=1}^\infty \theta_i</math> converges absolutely, it is necessarily the case that <math display="inline">\lim_{i \to \infty} \theta_i = 0,</math> <math display="inline">\lim_{i \to \infty} \sin \theta_i = 0,</math> and <math display="inline">\lim_{i \to \infty} \cos \theta_i = 1.</math> In particular, in these two identities an asymmetry appears that is not seen in the case of sums of finitely many angles: in each product, there are only finitely many sine factors but there are ] many cosine factors. Terms with infinitely many sine factors would necessarily be equal to zero.
	: <math> \cos\left(\sum_{i=1}^\infty \theta_i\right)
	=\sum_{\mathrm{even}\ k \ge 0} ~ (-1)^{k/2} ~~
	\sum_{ |A| = k }
	\left(\prod_{i \in A} \sin\theta_i \prod_{i \not \in A} \cos\theta_i\right) </math>
			When only finitely many of the angles <math>\theta_i</math> are nonzero then only finitely many of the terms on the right side are nonzero because all but finitely many sine factors vanish. Furthermore, in each term all but finitely many of the cosine factors are unity.
	where "|''A''| = ''k''" means the index ''A'' runs through the set of all subsets of size ''k'' of the set {&nbsp;1,&nbsp;2,&nbsp;3,&nbsp;...&nbsp;}.
			=== Tangents and cotangents of sums ===
	In these two identities an asymmetry appears that is not seen in the case of sums of finitely many terms: in each product, there are only finitely many sine factors and ]ly many cosine factors.
			Let <math>e_k</math> (for <math>k = 0, 1, 2, 3, \ldots</math>) be the {{mvar|k}}th-degree ] in the variables
			<math display="block">x_i = \tan \theta_i</math>
			for <math>i = 0, 1, 2, 3, \ldots,</math> that is,
			<math display=block>\begin{align}
	If only finitely many of the terms θ<sub>''i''</sub> are nonzero, then only finitely many of the terms on the right side will be nonzero because sine factors will vanish, and in each term, all but finitely many of the cosine factors will be unity.
			e_0 &= 1 \\
			e_1 &= \sum_i x_i &&= \sum_i \tan\theta_i \\
			e_2 &= \sum_{i<j} x_i x_j &&= \sum_{i<j} \tan\theta_i \tan\theta_j \\
			e_3 &= \sum_{i<j<k} x_i x_j x_k &&= \sum_{i<j<k} \tan\theta_i \tan\theta_j \tan\theta_k \\
			&\ \ \vdots &&\ \ \vdots
			\end{align}</math>
			Then
	=== Tangents of sums of finitely many terms ===
			<math display=block>\begin{align}
	Let ''x''<sub>''i''</sub> = tan(θ<sub>''i''</sub>&nbsp;), for ''i'' = 1,&nbsp;...,&nbsp;''n''. Let ''e''<sub>''k''</sub> be the ''k''th-degree ] in the variables ''x''<sub>''i''</sub>, ''i''&nbsp;=&nbsp;1,&nbsp;...,&nbsp;''n'', ''k''&nbsp;=&nbsp;0,&nbsp;...,&nbsp;''n''. Then
			{\tan}\Bigl(\sum_i \theta_i\Bigr)
			&= \frac{{\sin}\bigl(\sum_i \theta_i\bigr) / \prod_i \cos \theta_i}
			{{\cos}\bigl(\sum_i \theta_i\bigr) / \prod_i \cos \theta_i} \\
			&= \frac
			{\displaystyle
			\sum_{\text{odd}\ k \ge 1} (-1)^\frac{k-1}{2}
			\sum_{
			\begin{smallmatrix} A \subseteq \{1,2,3,\dots\} \\
			\left|A\right| = k\end{smallmatrix}}
			\prod_{i \in A} \tan\theta_i}
			{\displaystyle
			\sum_{\text{even}\ k \ge 0} ~ (-1)^\frac{k}{2} ~~
			\sum_{
			\begin{smallmatrix} A \subseteq \{1,2,3,\dots\} \\
			\left|A\right| = k\end{smallmatrix}}
			\prod_{i \in A} \tan\theta_i}
			= \frac{e_1 - e_3 + e_5 -\cdots}{e_0 - e_2 + e_4 - \cdots} \\
			{\cot}\Bigl(\sum_i \theta_i\Bigr)
	: <math>\tan(\theta_1+\cdots+\theta_n) = \frac{e_1 - e_3 + e_5 -\cdots}{e_0 - e_2 + e_4 - \cdots}, </math>
			&= \frac{e_0 - e_2 + e_4 - \cdots}{e_1 - e_3 + e_5 -\cdots}
			\end{align}</math>
			using the sine and cosine sum formulae above.
	the number of terms depending on ''n''.
			The number of terms on the right side depends on the number of terms on the left side.
	For example,
			For example:
	:<math> \begin{align} \tan(\theta_1 + \theta_2 + \theta_3)
			<math display="block">\begin{align}
	&{}= \frac{e_1 - e_3}{e_0 - e_2} = \frac{(x_1 + x_2 + x_3) \ - \ (x_1 x_2 x_3)}{
			\tan(\theta_1 + \theta_2) &
	1 \ - \ (x_1 x_2 + x_1 x_3 + x_2 x_3)}, \\ \\
			= \frac{ e_1 }{ e_0 - e_2 }
	\tan(\theta_1 + \theta_2 + \theta_3 + \theta_4)
	&{}= \frac{e_1 - e_3}{e_0 - e_2 + e_4} \\ \\		= \frac{ x_1 + x_2 }{ 1 \ - \ x_1 x_2 }
			= \frac{ \tan\theta_1 + \tan\theta_2 }{ 1 \ - \ \tan\theta_1 \tan\theta_2 },
	&{}= \frac{(x_1 + x_2 + x_3 + x_4) \ - \ (x_1 x_2 x_3 + x_1 x_2 x_4 + x_1 x_3 x_4 + x_2 x_3 x_4)}{
			\\
	1 \ - \ (x_1 x_2 + x_1 x_3 + x_1 x_4 + x_2 x_3 + x_2 x_4 + x_3 x_4) \ + \ (x_1 x_2 x_3 x_4)},\end{align} </math>
			\tan(\theta_1 + \theta_2 + \theta_3) &
			= \frac{ e_1 - e_3 }{ e_0 - e_2 }
			= \frac{ (x_1 + x_2 + x_3) \ - \ (x_1 x_2 x_3) }{ 1 \ - \ (x_1x_2 + x_1 x_3 + x_2 x_3) },
			\\
			\tan(\theta_1 + \theta_2 + \theta_3 + \theta_4) &
			= \frac{ e_1 - e_3 }{ e_0 - e_2 + e_4 } \\ &
			= \frac{ (x_1 + x_2 + x_3 + x_4) \ - \ (x_1 x_2 x_3 + x_1 x_2 x_4 + x_1 x_3 x_4 + x_2 x_3 x_4) }{ 1 \ - \ (x_1 x_2 + x_1 x_3 + x_1 x_4 + x_2 x_3 + x_2 x_4 + x_3 x_4) \ + \ (x_1 x_2 x_3 x_4) },
			\end{align}</math>
			and so on. The case of only finitely many terms can be proved by ].<ref>{{cite conference |last=Bronstein |first=Manuel |title=Simplification of real elementary functions |pages=207–211 |doi=10.1145/74540.74566 |book-title=Proceedings of the ACM-] 1989 International Symposium on Symbolic and Algebraic Computation |editor-first= G. H. |editor-last=Gonnet |conference=ISSAC '89 (Portland US-OR, 1989-07) |location=New York |publisher=] |year=1989 |isbn=0-89791-325-6}}</ref> The case of infinitely many terms can be proved by using some elementary inequalities.<ref>Michael Hardy. (2016). "On Tangents and Secants of Infinite Sums." ''The American Mathematical Monthly'', volume 123, number 7, 701–703. https://doi.org/10.4169/amer.math.monthly.123.7.701</ref>
	and so on. The general case can be proved by ].
			=== Secants and cosecants of sums ===
	==Multiple-angle formulae==
			<math display=block>\begin{align}
	{|class="wikitable" style="background-color: #FFFFFF;"
			{\sec}\Bigl(\sum_i \theta_i \Bigr) &= \frac{\prod_i \sec\theta_i}{e_0 - e_2 + e_4 - \cdots} \\
	!''T<sub>n</sub>'' is the ''n''th ]
			{\csc}\Bigl(\sum_i \theta_i \Bigr) &= \frac{\prod_i \sec\theta_i }{e_1 - e_3 + e_5 - \cdots}
	|<math>\cos n\theta =T_n (\cos \theta )\,</math><ref name="mathworld_multiple_angle">{{MathWorld|title=Multiple-Angle Formulas|urlname=Multiple-AngleFormulas}}</ref>
			\end{align}</math>
	|-
	!''S''<sub>''n''</sub> is the ''n''th ]
	|<math>\sin^2 n\theta = S_n (\sin^2\theta)\,</math>
	|-
	!], <math>i</math> is the ]
	|<math>\cos n\theta +i\sin n\theta=(\cos(\theta)+i\sin(\theta))^n \,</math>
	|}
			where <math>e_k</math> is the {{mvar|k}}th-degree ] in the {{mvar|n}} variables <math>x_i = \tan \theta_i,</math> <math>i = 1, \ldots, n,</math> and the number of terms in the denominator and the number of factors in the product in the numerator depend on the number of terms in the sum on the left.<ref>{{cite journal |last=Hardy |first=Michael |year=2016 |title=On Tangents and Secants of Infinite Sums |journal=American Mathematical Monthly |volume=123 |issue=7 |pages=701–703 |doi=10.4169/amer.math.monthly.123.7.701 |url=https://zenodo.org/record/1000408 }}</ref> The case of only finitely many terms can be proved by mathematical induction on the number of such terms.
	See also ].
			For example,
	===Double, triple and half-angle formulae===
	These can be shown by using either the sum and difference identities or the multiple-angle formulae.
			<math display=block>\begin{align}
	{|class="wikitable" style="background-color:#FFFFFF;"
			\sec(\alpha+\beta+\gamma)
	!colspan="4"| Double-angle formulae <ref name="mathworld_double_angle">{{MathWorld|title=Double-Angle Formulas|urlname=Double-AngleFormulas}}</ref>
			&= \frac{\sec\alpha \sec\beta \sec\gamma}
	|-
			{1 - \tan\alpha\tan\beta - \tan\alpha\tan\gamma - \tan\beta\tan\gamma} \\
	|style="vertical-align:top"|<math>\begin{align}
			\csc(\alpha+\beta+\gamma)
	\sin 2\theta &= 2 \sin \theta \cos \theta \ \\ &= \frac{2 \tan \theta} {1 + \tan^2 \theta}
			&= \frac{\sec\alpha \sec\beta \sec\gamma}
			{\tan\alpha + \tan\beta + \tan\gamma - \tan\alpha\tan\beta\tan\gamma}.
	\end{align}</math>		\end{align}</math>
			=== Ptolemy's theorem ===
	|<math>\begin{align}
			{{Main|Ptolemy's theorem}}
	\cos 2\theta &= \cos^2 \theta - \sin^2 \theta \\ &= 2 \cos^2 \theta - 1 \\
			{{See also|History of trigonometry#Classical antiquity}}
	&= 1 - 2 \sin^2 \theta \\ &= \frac{1 - \tan^2 \theta} {1 + \tan^2 \theta}
	\end{align}</math>
			]
	|<math>\tan 2\theta = \frac{2 \tan \theta} {1 - \tan^2 \theta}\, </math>
			Ptolemy's theorem is important in the history of trigonometric identities, as it is how results equivalent to the sum and difference formulas for sine and cosine were first proved. It states that in a cyclic quadrilateral <math>ABCD</math>, as shown in the accompanying figure, the sum of the products of the lengths of opposite sides is equal to the product of the lengths of the diagonals. In the special cases of one of the diagonals or sides being a diameter of the circle, this theorem gives rise directly to the angle sum and difference trigonometric identities.<ref name="cut-the-knot.org">{{cite web | url=https://www.cut-the-knot.org/proofs/sine_cosine.shtml | title=Sine, Cosine, and Ptolemy's Theorem }}</ref> The relationship follows most easily when the circle is constructed to have a diameter of length one, as shown here.
	|<math>\cot 2\theta = \frac{\cot \theta - \tan \theta}{2}\,</math>
			By ], <math> \angle DAB</math> and <math> \angle DCB</math> are both right angles. The right-angled triangles <math>DAB</math> and <math>DCB</math> both share the hypotenuse <math>\overline{BD}</math> of length 1. Thus, the side <math>\overline{AB} = \sin \alpha</math>, <math>\overline{AD} = \cos \alpha</math>, <math>\overline{BC} = \sin \beta</math> and <math>\overline{CD} = \cos \beta</math>.
	|-
	!colspan="4"| Triple-angle formulae <ref name="mathworld_multiple_angle">{{MathWorld|title=Multiple-Angle Formulas|urlname=Multiple-AngleFormulas}}</ref>
	|-
	|<math>\sin 3\theta = 3 \sin \theta- 4 \sin^3\theta \,</math>
	|<math>\cos 3\theta = 4 \cos^3\theta - 3 \cos \theta \,</math>
	|<math>\tan 3\theta = \frac{3 \tan\theta - \tan^3\theta}{1 - 3 \tan^2\theta}</math>
	|&nbsp;
	|-
	!colspan="4"| Half-angle formulae <ref name="mathworld_half_angle">{{MathWorld|title=Half-Angle Formulas|urlname=Half-AngleFormulas}}</ref>
	|-
	|<math>\sin \tfrac{\theta}{2} = \pm\, \sqrt{\frac{1 - \cos \theta}{2}}</math>
	|<math>\cos \tfrac{\theta}{2} = \pm\, \sqrt{\frac{1 + \cos\theta}{2}}</math>
	|<math>\begin{align} \tan \tfrac{\theta}{2} &= \csc \theta - \cot \theta \\ &= \pm\, \sqrt{1 - \cos \theta \over 1 + \cos \theta} \\ &= \frac{\sin \theta}{1 + \cos \theta} \\ &= \frac{1-\cos \theta}{\sin \theta} \end{align}</math>
	|<math>\cot \tfrac{\theta}{2} = \csc \theta + \cot \theta</math>
			By the ] theorem, the central angle subtended by the chord <math>\overline{AC}</math> at the circle's center is twice the angle <math> \angle ADC</math>, i.e. <math>2(\alpha + \beta)</math>. Therefore, the symmetrical pair of red triangles each has the angle <math>\alpha + \beta</math> at the center. Each of these triangles has a hypotenuse of length <math display="inline">\frac{1}{2}</math>, so the length of <math>\overline{AC}</math> is <math display="inline">2 \times \frac{1}{2} \sin(\alpha + \beta)</math>, i.e. simply <math>\sin(\alpha + \beta)</math>. The quadrilateral's other diagonal is the diameter of length 1, so the product of the diagonals' lengths is also <math>\sin(\alpha + \beta)</math>.
	|}
	''See also ].''
			When these values are substituted into the statement of Ptolemy's theorem that <math>|\overline{AC}|\cdot |\overline{BD}|=|\overline{AB}|\cdot |\overline{CD}|+|\overline{AD}|\cdot |\overline{BC}|</math>, this yields the angle sum trigonometric identity for sine: <math> \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta </math>. The angle difference formula for <math> \sin(\alpha - \beta)</math> can be similarly derived by letting the side <math>\overline{CD}</math> serve as a diameter instead of <math>\overline{BD}</math>.<ref name="cut-the-knot.org"/>
	== Power-reduction formulae ==
	Obtained by solving the second and third versions of the cosine double-angle formula.
			== Multiple-angle and half-angle formulae ==
	{|class="wikitable" style="background-color: #FFFFFF"
			{|class="wikitable" style="color: inherit; background-color:var(--background-color-base);"
	!Sine
			! {{mvar|T<sub>n</sub>}} is the {{mvar|n}}th ]
	|<math>\sin^2\theta = \frac{1 - \cos 2\theta}{2}</math>
			| <math>\cos (n\theta) = T_n (\cos \theta )</math><ref name="mathworld_multiple_angle">{{MathWorld|title=Multiple-Angle Formulas|urlname=Multiple-AngleFormulas}}</ref>
	|<math>\sin^3\theta = \frac{3 \sin\theta - \sin 3\theta}{4}</math>
	|-		|-
			! ], {{mvar|i}} is the ]
	!Cosine
	|<math>\cos^2\theta = \frac{1 + \cos 2\theta}{2}</math>		| <math>\cos (n\theta) +i\sin (n\theta)=(\cos \theta +i\sin \theta)^n</math><ref>Abramowitz and Stegun, p.&nbsp;74, 4.3.48</ref>
	|<math>\cos^3\theta = \frac{3 \cos\theta + \cos 3\theta}{4}</math>
	|-
	!Other
	|<math>\sin^2\theta \cos^2\theta = \frac{1 - \cos 4\theta}{8}</math>
	|<math>\sin^3\theta \cos^3\theta = \frac{\sin^3 2\theta}{8}</math>
	|}		|}
			=== Multiple-angle formulae ===
	==Product-to-sum and sum-to-product identities==
	The product-to-sum identies can be proven by expanding their right-hand sides using the ].
			==== Double-angle formulae ====
	{|
			]
	|style="vertical-align:top"|
	{|class="wikitable" style="background-color: #FFFFFF"
	!Product-to-sum
	|-
	| <math>\cos \theta \cos \phi = {\cos(\theta - \phi) + \cos(\theta + \phi) \over 2}</math>
	|-
	| <math>\sin \theta \sin \phi = {\cos(\theta - \phi) - \cos(\theta + \phi) \over 2}</math>
	|-
	| <math>\sin \theta \cos \phi = {\sin(\theta + \phi) + \sin(\theta - \phi) \over 2}</math>
	|}
	|
	{|class="wikitable" style="background-color: #FFFFFF"
	!Sum-to-product
	|-
	|<math>\sin \theta + \sin \phi = 2 \sin\left( \frac{\theta + \phi}{2} \right) \cos\left( \frac{\theta - \phi}{2} \right)</math>
	|-
	|<math>\cos \theta + \cos \phi = 2 \cos\left( \frac{\theta + \phi} {2} \right) \cos\left( \frac{\theta - \phi}{2} \right)</math>
	|-
	|<math>\cos \theta - \cos \phi = -2\sin\left( {\theta + \phi \over 2}\right) \sin\left({\theta - \phi \over 2}\right)</math>
	|-
	|<math>\sin \theta - \sin \phi = 2 \cos\left({\theta + \phi \over 2}\right) \sin\left({\theta - \phi\over 2}\right) \; </math>
	|}
	|}
	===Other related identities===
	If ''x'', ''y'', and ''z'' are the three angles of any triangle, or in other words
			Formulae for twice an angle.<ref name=STM1>{{harvnb|Selby|1970|loc=pg. 190}}</ref>
	:<math>\mbox{if }x + y + z = \pi = \mbox{half circle,}\, </math>
			{{startplainlist}}
	::<math>\mbox{then }\tan(x) + \tan(y) + \tan(z) = \tan(x)\tan(y)\tan(z).\,</math>
			* <math>\sin (2\theta) = 2 \sin \theta \cos \theta = (\sin \theta +\cos \theta)^2 - 1 = \frac{2 \tan \theta} {1 + \tan^2 \theta}</math>
			* <math>\cos (2\theta) = \cos^2 \theta - \sin^2 \theta = 2 \cos^2 \theta - 1 = 1 - 2 \sin^2 \theta = \frac{1 - \tan^2 \theta} {1 + \tan^2 \theta}</math>
			* <math>\tan (2\theta) = \frac{2 \tan \theta} {1 - \tan^2 \theta}</math>
			* <math>\cot (2\theta) = \frac{\cot^2 \theta - 1}{2 \cot \theta} = \frac{1 - \tan^2 \theta} {2 \tan \theta}</math>
			* <math>\sec (2\theta) = \frac{\sec^2 \theta}{2 - \sec^2 \theta} = \frac{1 + \tan^2 \theta} {1 - \tan^2 \theta}</math>
			* <math>\csc (2\theta) = \frac{\sec \theta \csc \theta}{2} = \frac{1 + \tan^2 \theta} {2 \tan \theta}</math>
			{{endplainlist}}
			==== Triple-angle formulae ====
	(If any of ''x'', ''y'', ''z'' is a right angle, one should take both sides to be ∞. This is neither +∞ nor &minus;∞; for present purposes it makes sense to add just one point at infinity to the ], that is approached by tan(θ) as tan(θ) either increases through positive values or decreases through negative values. This is a ] of the real line.)
			Formulae for triple angles.<ref name=STM1 />
			{{startplainlist}}
	:<math>\mbox{If }x + y + z = \pi = \mbox{half circle,}\, </math>
			* <math>\sin (3\theta) =3\sin\theta - 4\sin^3\theta = 4\sin\theta\sin\left(\frac{\pi}{3} -\theta\right)\sin\left(\frac{\pi}{3} + \theta\right)</math>
			* <math>\cos (3\theta) = 4 \cos^3\theta - 3 \cos\theta =4\cos\theta\cos\left(\frac{\pi}{3} -\theta\right)\cos\left(\frac{\pi}{3} + \theta\right)</math>
			* <math>\tan (3\theta) = \frac{3 \tan\theta - \tan^3\theta}{1 - 3 \tan^2\theta} = \tan \theta\tan\left(\frac{\pi}{3} - \theta\right)\tan\left(\frac{\pi}{3} + \theta\right)</math>
			* <math>\cot (3\theta) = \frac{3 \cot\theta - \cot^3\theta}{1 - 3 \cot^2\theta}</math>
			* <math>\sec (3\theta) = \frac{\sec^3\theta}{4-3\sec^2\theta}</math>
			* <math>\csc (3\theta) = \frac{\csc^3\theta}{3\csc^2\theta-4}</math>
			{{endplainlist}}
			==== Multiple-angle formulae ====
	::<math>\mbox{then }\sin(2x) + \sin(2y) + \sin(2z) = 4\sin(x)\sin(y)\sin(z).\,</math>
			Formulae for multiple angles.<ref>{{Cite web|last=Weisstein|first=Eric W.|title=Multiple-Angle Formulas|url=https://mathworld.wolfram.com/|access-date=2022-02-06|website=mathworld.wolfram.com|language=en}}</ref>
			{{startplainlist}}
	=== Ptolemy's theorem ===
			* <math>\begin{align}
			\sin(n\theta) &= \sum_{k\text{ odd}} (-1)^\frac{k-1}{2} {n \choose k}\cos^{n-k} \theta \sin^k \theta =
			\sin\theta\sum_{i=0}^{(n+1)/2}\sum_{j=0}^{i} (-1)^{i-j} {n \choose 2i + 1}{i \choose j}
			\cos^{n-2(i-j)-1} \theta \\
			{}&=\sin(\theta)\cdot\sum_{k=0}^{\left\lfloor\frac{n-1}{2}\right\rfloor}(-1)^k\cdot {(2\cdot \cos(\theta))}^{n-2k-1}\cdot {n-k-1 \choose k} \\
			{}&=2^{(n-1)} \prod_{k=0}^{n-1} \sin(k\pi/n+\theta)
			\end{align}</math>
			* <math> \begin{align}\cos(n\theta) &= \sum_{k\text{ even}} (-1)^\frac{k}{2} {n \choose k}\cos^{n-k} \theta \sin^k \theta =
			\sum_{i=0}^{n/2}\sum_{j=0}^{i} (-1)^{i-j} {n \choose 2i}{i \choose j} \cos^{n-2(i-j)} \theta \\
			{} &= \sum_{k=0}^{\left\lfloor\frac{n}{2}\right\rfloor} (-1)^k\cdot {(2\cdot \cos(\theta))}^{n-2k}\cdot {n-k \choose k}\cdot\frac{n}{2n-2k}
			\end{align}</math>
			* <math>\cos((2n+1)\theta)=(-1)^n 2^{2n}\prod_{k=0}^{2n}\cos(k\pi/(2n+1)-\theta)</math>
			* <math>\cos(2 n \theta)=(-1)^n 2^{2n-1} \prod_{k=0}^{2n-1} \cos((1+2k)\pi/(4n)-\theta)</math>
			* <math>\tan(n\theta) = \frac{\sum_{k\text{ odd}} (-1)^\frac{k-1}{2} {n \choose k}\tan^k \theta}{\sum_{k\text{ even}} (-1)^\frac{k}{2} {n \choose k}\tan^k \theta}</math>
			{{endplainlist}}
			==== Chebyshev method ====
			The ] method is a ] ] for finding the {{mvar|n}}th multiple angle formula knowing the <math>(n-1)</math>th and <math>(n-2)</math>th values.<ref>{{cite web|last=Ward|first=Ken|website=Ken Ward's Mathematics Pages|title=Multiple angles recursive formula|url=http://trans4mind.com/personal_development/mathematics/trigonometry/multipleAnglesRecursiveFormula.htm}}</ref>
			<math>\cos(nx)</math> can be computed from <math>\cos((n-1)x)</math>, <math>\cos((n-2)x)</math>, and <math>\cos(x)</math> with
			<math display="block">\cos(nx)=2 \cos x \cos((n-1)x) - \cos((n-2)x).</math>
			This can be proved by adding together the formulae
	:<math> \mbox{If }w + x + y + z = \pi = \mbox{half circle,} \, </math>
	::<math>\begin{align} \mbox{then }		<math display="block">\begin{align}
	& \sin(w + x)\sin(x + y) \\		\cos ((n-1)x + x) &= \cos ((n-1)x) \cos x-\sin ((n-1)x) \sin x \\
	&{} = \sin(x + y)\sin(y + z) \\		\cos ((n-1)x - x) &= \cos ((n-1)x) \cos x+\sin ((n-1)x) \sin x
	&{} = \sin(y + z)\sin(z + w) \\
	&{} = \sin(z + w)\sin(w + x) = \sin(w)\sin(y) + \sin(x)\sin(z).
	\end{align}</math>		\end{align}</math>
			It follows by induction that <math>\cos(nx)</math> is a polynomial of <math>\cos x,</math> the so-called Chebyshev polynomial of the first kind, see ].
	(The first three equalities are trivial; the fourth is the substance of this identity.) Essentially this is ] adapted to the language of trigonometry.
			Similarly, <math>\sin(nx)</math> can be computed from <math>\sin((n-1)x),</math> <math>\sin((n-2)x),</math> and <math>\cos x</math> with
	==Linear combinations==
			<math display="block">\sin(nx)=2 \cos x \sin((n-1)x)-\sin((n-2)x)</math>
			This can be proved by adding formulae for <math>\sin((n-1)x+x)</math> and <math>\sin((n-1)x-x).</math>
			Serving a purpose similar to that of the Chebyshev method, for the tangent we can write:
	For some purposes it is important to know that any linear combination of sine waves of the same period but different ] is also a sine wave with the same period, but a different phase shift. In the case of a linear combination of a sine and cosine wave, we have
	:<math>a\sin x+b\cos x=\sqrt{a^2+b^2}\cdot\sin(x+\varphi)\,</math>		<math display="block">\tan (nx) = \frac{\tan ((n-1)x) + \tan x}{1- \tan ((n-1)x) \tan x}\,.</math>
			=== Half-angle formulae ===
	where
			<math display=block>\begin{align}
	:<math>\varphi = \arctan \left(\frac{b}{a}\right)</math>
			\sin \frac{\theta}{2} &= \sgn\left(\sin\frac\theta2\right) \sqrt{\frac{1 - \cos \theta}{2}} \\
			\cos \frac{\theta}{2} &= \sgn\left(\cos\frac\theta2\right) \sqrt{\frac{1 + \cos\theta}{2}} \\
	More generally, for an arbitrary phase shift, we have
			\tan \frac{\theta}{2}
	:<math>a\sin x+b\sin(x+\alpha)= c \sin(x+\beta)\,</math>
			&= \frac{1 - \cos \theta}{\sin \theta}
			= \frac{\sin \theta}{1 + \cos \theta}
			= \csc \theta - \cot \theta
			= \frac{\tan\theta}{1 + \sec{\theta}} \\
			&= \sgn(\sin \theta) \sqrt\frac{1 - \cos \theta}{1 + \cos \theta}
	where
			= \frac{-1 + \sgn(\cos \theta) \sqrt{1+\tan^2\theta}}{\tan\theta} \\
			\cot \frac{\theta}{2}
	:<math>
	c = \sqrt{a^2 + b^2 +2ab\cos \alpha},</math>		&= \frac{1 + \cos \theta}{\sin \theta}
			= \frac{\sin \theta}{1 - \cos \theta}
			= \csc \theta + \cot \theta
			= \sgn(\sin \theta) \sqrt\frac{1 + \cos \theta}{1 - \cos \theta} \\
			\sec \frac{\theta}{2}
	and
			&= \sgn\left(\cos\frac\theta2\right) \sqrt{\frac{2}{1 + \cos\theta}} \\
			\csc \frac{\theta}{2}
	:<math>
	\beta = {\rm arctan} \left(\frac{b\sin \alpha}{a + b\cos \alpha}\right).		&= \sgn\left(\sin\frac\theta2\right) \sqrt{\frac{2}{1 - \cos\theta}} \\
	</math>
			\end{align}</math>
	*note: arcsin, arccos, arctan are all inverses.
			<ref name="ReferenceA">{{AS ref|4, eqn 4.3.20-22|72}}</ref><ref name="mathworld_half_angle">{{MathWorld|title=Half-Angle Formulas|urlname=Half-AngleFormulas}}</ref>
			Also
	==Other sums of trigonometric functions==
			<math display=block>\begin{align}
			\tan\frac{\eta\pm\theta}{2} &= \frac{\sin\eta \pm \sin\theta}{\cos\eta + \cos\theta} \\
			\tan\left(\frac{\theta}{2} + \frac{\pi}{4}\right) &= \sec\theta + \tan\theta \\
			\sqrt{\frac{1 - \sin\theta}{1 + \sin\theta}} &= \frac{\left|1 - \tan\frac{\theta}{2}\right|}{\left|1 + \tan\frac{\theta}{2}\right|}
			\end{align}</math>
			=== Table ===
	Sum of sines and cosines with arguments in arithmetic progression:
			<!-- ], ], ], ], ], and ] redirect here -->
			{{See also|Tangent half-angle formula}}
			These can be shown by using either the sum and difference identities or the multiple-angle formulae.
			<div style="overflow-x:auto;">
	:<math>\sin{\varphi} + \sin{(\varphi + \alpha)} + \sin{(\varphi + 2\alpha)} +
			{|class="wikitable" style="background-color:var(--background-color-base);"
	\cdots + \sin{(\varphi + n\alpha)}=\frac{\sin{\left(\frac{(n+1) \alpha}{2}\right)} \cdot \sin{(\varphi + \frac{n \alpha}{2})}}{\sin{\frac{\alpha}{2}}}.</math>
			! !! Sine !! Cosine !! Tangent !! Cotangent
			|-
			! Double-angle formula<ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.24–26</ref><ref name="mathworld_double_angle">{{MathWorld|title=Double-Angle Formulas|urlname=Double-AngleFormulas}}</ref>
			| <math>\begin{align}
			\sin (2\theta) &= 2 \sin \theta \cos \theta \ \\
			&= \frac{2 \tan \theta} {1 + \tan^2 \theta}
			\end{align}</math>
			| <math>\begin{align}
			\cos (2\theta) &= \cos^2 \theta - \sin^2 \theta \\
			&= 2 \cos^2 \theta - 1 \\
			&= 1 - 2 \sin^2 \theta \\
			&= \frac{1 - \tan^2 \theta} {1 + \tan^2 \theta}
			\end{align}</math>
			| <math>\tan (2\theta) = \frac{2 \tan \theta} {1 - \tan^2 \theta}</math>
			| <math>\cot (2\theta) = \frac{\cot^2 \theta - 1}{2 \cot \theta}</math>
			|-
			! Triple-angle formula<ref name="mathworld_multiple_angle" /><ref name="Stegun p. 72, 4">Abramowitz and Stegun, p.&nbsp;72, 4.3.27–28</ref>
			| <math>\begin{align}
			\sin (3\theta) &= - \sin^3\theta + 3 \cos^2\theta \sin\theta\\
			&= - 4\sin^3\theta + 3\sin\theta
			\end{align}</math>
			| <math>\begin{align}
			\cos (3\theta) &= \cos^3\theta - 3 \sin^2 \theta\cos \theta \\
			&= 4 \cos^3\theta - 3 \cos\theta
			\end{align}</math>
			| <math>\tan (3\theta) = \frac{3 \tan\theta - \tan^3\theta}{1 - 3 \tan^2\theta}</math>
			| <math>\cot (3\theta) = \frac{3 \cot\theta - \cot^3\theta}{1 - 3 \cot^2\theta}</math>
			|-
			! Half-angle formula<ref name="ReferenceA" /><ref name="mathworld_half_angle" />
			| <math>\begin{align}
			&\sin \frac{\theta}{2} = \sgn\left(\sin\frac\theta2\right) \sqrt{\frac{1 - \cos \theta}{2}} \\ \\
			&\left(\text{or }\sin^2\frac{\theta}{2} = \frac{1 - \cos\theta}{2}\right)
			\end{align}</math>
			| <math>\begin{align}
			&\cos \frac{\theta}{2} = \sgn\left(\cos\frac\theta2\right) \sqrt{\frac{1 + \cos\theta}{2}} \\ \\
			&\left(\text{or } \cos^2\frac{\theta}{2} = \frac{1 + \cos\theta}{2}\right)
			\end{align}</math>
			| <math>\begin{align}
			\tan \frac{\theta}{2}
			&= \csc \theta - \cot \theta \\
			&= \pm\, \sqrt\frac{1 - \cos \theta}{1 + \cos \theta} \\
			&= \frac{\sin \theta}{1 + \cos \theta} \\
			&= \frac{1 - \cos \theta}{\sin \theta} \\
			\tan\frac{\eta + \theta}{2} &= \frac{\sin\eta + \sin\theta}{\cos\eta + \cos\theta} \\
			\tan\left(\frac{\theta}{2} + \frac{\pi}{4}\right) &= \sec\theta + \tan\theta \\
			\sqrt{\frac{1 - \sin\theta}{1 + \sin\theta}}
			&= \frac{\left|1 - \tan\frac{\theta}{2}\right|}{\left|1 + \tan\frac{\theta}{2}\right|} \\
			\tan\frac{\theta}{2} &= \frac{\tan\theta}{1 + \sqrt{1 + \tan^2\theta}} \\
			&\text{for } \theta \in \left(-\tfrac{\pi}{2},\tfrac{\pi}{2} \right)
			\end{align}</math>
			| <math>\begin{align}
			\cot \frac{\theta}{2}
			&= \csc \theta + \cot \theta \\
			&= \pm\, \sqrt\frac{1 + \cos \theta}{1 - \cos \theta} \\
			&= \frac{\sin \theta}{1 - \cos \theta} \\
			&= \frac{1 + \cos \theta}{\sin \theta}
			\end{align}</math>
			|}
			</div>
			The fact that the triple-angle formula for sine and cosine only involves powers of a single function allows one to relate the geometric problem of a ] of ] to the algebraic problem of solving a ], which allows one to prove that ] using the given tools.
			A formula for computing the trigonometric identities for the one-third angle exists, but it requires finding the zeroes of the ] {{math|1=4''x''<sup>3</sup> − 3''x'' + ''d'' = 0}}, where <math>x</math> is the value of the cosine function at the one-third angle and {{mvar|d}} is the known value of the cosine function at the full angle. However, the ] of this equation is positive, so this equation has three real roots (of which only one is the solution for the cosine of the one-third angle). ] to a real ], as they use intermediate complex numbers under the ]s.
	:<math>\cos{\varphi} + \cos{(\varphi + \alpha)} + \cos{(\varphi + 2\alpha)} +
	\cdots + \cos{(\varphi + n\alpha)}=\frac{\sin{\left(\frac{(n+1) \alpha}{2}\right)} \cdot \cos{(\varphi + \frac{n \alpha}{2})}}{\sin{\frac{\alpha}{2}}}.</math>
			== Power-reduction formulae ==
	For any ''a'' and ''b'':
			Obtained by solving the second and third versions of the cosine double-angle formula.
	: <math>a \cos(x) + b \sin(x) = \sqrt{ a^2 + b^2 } \cos(x - \arctan(b, a)) \;</math>
			<div class="noresize">
	where arctan(''y'', ''x'') is the generalization of arctan(''y''/''x'') which covers the entire circular range (see also the account of this same identity in "symmetry, periodicity, and shifts" above for this generalization of arctan).
			{|class="wikitable"
			!Sine
			!Cosine
			!Other
			|-
			|<math>\sin^2\theta = \frac{1 - \cos (2\theta)}{2}</math>
			|<math>\cos^2\theta = \frac{1 + \cos (2\theta)}{2}</math>
			|<math>\sin^2\theta \cos^2\theta = \frac{1 - \cos (4\theta)}{8}</math>
			|-
			|<math>\sin^3\theta = \frac{3 \sin\theta - \sin (3\theta)}{4}</math>
			|<math>\cos^3\theta = \frac{3 \cos\theta + \cos (3\theta)}{4}</math>
			|<math>\sin^3\theta \cos^3\theta = \frac{3\sin (2\theta) - \sin (6\theta)}{32}</math>
			|-
			|<math>\sin^4\theta = \frac{3 - 4 \cos (2\theta) + \cos (4\theta)}{8}</math>
			|<math>\cos^4\theta = \frac{3 + 4 \cos (2\theta) + \cos (4\theta)}{8}</math>
			|<math>\sin^4\theta \cos^4\theta = \frac{3-4\cos (4\theta) + \cos (8\theta)}{128}</math>
			|-
			|<math>\sin^5\theta = \frac{10 \sin\theta - 5 \sin (3\theta) + \sin (5\theta)}{16}</math>
			|<math>\cos^5\theta = \frac{10 \cos\theta + 5 \cos (3\theta) + \cos (5\theta)}{16}</math>
			|<math>\sin^5\theta \cos^5\theta = \frac{10\sin (2\theta) - 5\sin (6\theta) + \sin (10\theta)}{512}</math>
			|}
			</div>
			{{stack |float=left |] }}
	:<math>\tan(x) + \sec(x) = \tan\left({x \over 2} + {\pi \over 4}\right).</math>
			{{stack |float=left |] }}
			{{clear}}
			In general terms of powers of <math>\sin \theta</math> or <math>\cos \theta</math> the following is true, and can be deduced using ], ] and the ].
	The above identity is sometimes convenient to know when thinking about the ].
			{|class="wikitable"
	If <math>x</math>, <math>y</math>, and <math>z</math> are the three angles of any triangle, i.e. if <math>x + y + z = \pi</math>, then
			! scope="col" | if ''n'' is&nbsp;...
			! scope="col" | <math>\cos^n \theta</math>
			! scope="col" | <math>\sin^n \theta</math>
			|-
			! scope="row" | ''n'' is odd
			|<math>\cos^n\theta = \frac{2}{2^n} \sum_{k=0}^{\frac{n-1}{2}} \binom{n}{k} \cos{\big((n-2k)\theta\big)}</math>
			|<math>\sin^n\theta = \frac{2}{2^n} \sum_{k=0}^{\frac{n-1}{2}} (-1)^{\left(\frac{n-1}{2}-k\right)} \binom{n}{k} \sin{\big((n-2k)\theta\big)}</math>
			|-
			! scope="row" | ''n'' is even
			|<math>\cos^n\theta = \frac{1}{2^n} \binom{n}{\frac{n}{2}} + \frac{2}{2^n} \sum_{k=0}^{\frac{n}{2}-1} \binom{n}{k} \cos{\big((n-2k)\theta\big)}</math>
			|<math>\sin^n\theta = \frac{1}{2^n} \binom{n}{\frac{n}{2}} + \frac{2}{2^n} \sum_{k=0}^{\frac{n}{2}-1} (-1)^{\left(\frac{n}{2}-k\right)} \binom{n}{k} \cos{\big((n-2k)\theta\big)}</math>
			|}
			==Product-to-sum and sum-to-product identities==<!-- ] links to this section -->
	:<math>\cot(x)\cot(y) + \cot(y)\cot(z) + \cot(z)\cot(x) = 1.\,</math>
			] ]]
			The product-to-sum identities<ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.31–33</ref> or ] formulae can be proven by expanding their right-hand sides using the ]. Historically, the first four of these were known as '''Werner's formulas''', after ] who used them for astronomical calculations.<ref>{{Cite book |last=Eves |first=Howard |title=An introduction to the history of mathematics |date=1990 |publisher=Saunders College Pub |isbn=0-03-029558-0 |edition=6th |location=Philadelphia |page=309 |oclc=20842510}}</ref> See ] for an application of the product-to-sum formulae, and ] and ] for applications of the sum-to-product formulae.
			===Product-to-sum identities===
	==Inverse trigonometric functions==
	:<math> \arcsin(x)+\arccos(x)=\pi/2\;</math>
			{{startplainlist}}
	:<math> \arctan(x)+\arccot(x)=\pi/2.\;</math>
			* <math>\begin{align}
			\cos \theta\, \cos \varphi &= \tfrac12\bigl(\!\!~\cos(\theta - \varphi) + \cos(\theta + \varphi)\bigr) \\
			\sin \theta\, \sin \varphi &= \tfrac12\bigl(\!\!~\cos(\theta - \varphi) - \cos(\theta + \varphi)\bigr) \\
			\sin \theta\, \cos \varphi &= \tfrac12\bigl(\!\!~\sin(\theta + \varphi) + \sin(\theta - \varphi)\bigr) \\
			\cos \theta\, \sin \varphi &= \tfrac12\bigl(\!\!~\sin(\theta + \varphi) - \sin(\theta - \varphi)\bigr)
			\end{align}</math>
			* <math>\tan \theta\, \tan \varphi =\frac{\cos(\theta-\varphi)-\cos(\theta+\varphi)}{\cos(\theta-\varphi)+\cos(\theta+\varphi)}</math>
			* <math>\tan \theta\, \cot \varphi = \frac{\sin(\theta + \varphi) + \sin(\theta - \varphi)}{\sin(\theta + \varphi) - \sin(\theta - \varphi)}</math>
			* <math>\begin{align} \prod_{k=1}^n \cos \theta_k & = \frac{1}{2^n}\sum_{e\in S} \cos(e_1\theta_1+\cdots+e_n\theta_n) \\
			& \text{where }e = (e_1,\ldots,e_n) \in S=\{1,-1\}^n
			\end{align}</math>
			* <math>
			\prod_{k=1}^n \sin\theta_k=\frac{(-1)^{\left\lfloor\frac
			{n}{2}\right\rfloor}}{2^n}\begin{cases}
			\displaystyle\sum_{e\in S}\cos(e_1\theta_1+\cdots+e_n\theta_n)\prod_{j=1}^n e_j \;\text{if}\; n\; \text{is even},\\
			\displaystyle\sum_{e\in S}\sin(e_1\theta_1+\cdots+e_n\theta_n)\prod_{j=1}^n e_j \;\text{if}\; n\; \text{is odd}
			\end{cases}</math>
			{{endplainlist}}
			===Sum-to-product identities===
	:<math>\arctan(x)+\arctan(1/x)=\left\{\begin{matrix} \pi/2, & \mbox{if }x > 0 \\ -\pi/2, & \mbox{if }x < 0 \end{matrix}\right.</math>
			]
			The sum-to-product identities are as follows:<ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.34–39</ref>
			{{startplainlist}}
	:<math>\arctan(x)+\arctan(y)=\arctan\left(\frac{x+y}{1-xy}\right)+\left\{\begin{matrix} \pi, & \mbox{if }x,y>0 \\ -\pi, & \mbox{if }x,y<0 \\ 0, & \mbox{otherwise } \end{matrix}\right.</math>
			* <math>\sin \theta \pm \sin \varphi = 2 \sin\left( \frac{\theta \pm \varphi}{2} \right) \cos\left( \frac{\theta \mp \varphi}{2} \right)</math>
			* <math>\cos \theta + \cos \varphi = 2 \cos\left( \frac{\theta + \varphi} {2} \right) \cos\left( \frac{\theta - \varphi}{2} \right)</math>
			* <math>\cos \theta - \cos \varphi = -2\sin\left( \frac{\theta + \varphi}{2}\right) \sin\left(\frac{\theta - \varphi}{2}\right)</math>
			* <math>\tan\theta\pm\tan\varphi=\frac{\sin(\theta\pm \varphi)}{\cos\theta\,\cos\varphi}</math>
			{{endplainlist}}
			=== Hermite's cotangent identity ===
	{{col-start}}
			{{Main|Hermite's cotangent identity}}
	{{col-2}}
	:<math>\sin=\sqrt{1-x^2} \,</math>
	:<math>\sin=\frac{x}{\sqrt{1+x^2}}</math>
	:<math>\cos=\frac{1}{\sqrt{1+x^2}}</math>
	{{col-2}}
	:<math>\cos=\sqrt{1-x^2} \,</math>
	:<math>\tan=\frac{x}{\sqrt{1 - x^2}}</math>
	:<math>\tan=\frac{\sqrt{1 - x^2}}{x}</math>
	{{col-end}}
			] demonstrated the following identity.<ref>{{cite journal|first=Warren P. |last=Johnson |title=Trigonometric Identities à la Hermite |journal=] |volume=117 |issue=4 |date=Apr 2010 |pages=311–327 |doi=10.4169/000298910x480784|s2cid=29690311 }}</ref> Suppose <math>a_1, \ldots, a_n</math> are ]s, no two of which differ by an integer multiple of&nbsp;{{pi}}. Let
	==Relation to the complex exponential function==
			<math display="block">A_{n,k} = \prod_{\begin{smallmatrix} 1 \le j \le n \\ j \neq k \end{smallmatrix}} \cot(a_k - a_j)</math>
	:<math>e^{ix} = \cos(x) + i\sin(x)\,</math> (]),
			(in particular, <math>A_{1,1},</math> being an ], is&nbsp;1). Then
	:<math>e^{-ix} = \cos(-x) + i\sin(-x) = \cos(x) - i\sin(x)\,</math>
			<math display="block">\cot(z - a_1)\cdots\cot(z - a_n) = \cos\frac{n\pi}{2} + \sum_{k=1}^n A_{n,k} \cot(z - a_k).</math>
	:<math>e^{i\pi} = -1\,</math>
			The simplest non-trivial example is the case&nbsp;{{math|1=''n''&nbsp;=&nbsp;2}}:
	: <math>\cos(x) = \frac{e^{ix} + e^{-ix}}{2} \;</math>
			<math display="block">\cot(z - a_1)\cot(z - a_2) = -1 + \cot(a_1 - a_2)\cot(z - a_1) + \cot(a_2 - a_1)\cot(z - a_2).</math>
	: <math>\sin(x) = \frac{e^{ix} - e^{-ix}}{2i} \;</math>
			=== Finite products of trigonometric functions ===
	where ''i''² = &minus;1.
			For ] integers {{mvar|n}}, {{mvar|m}}
	==="cis"===
	{{split-section|cis (mathematics)}}
	Occasionally one sees the notation
	:<math>\operatorname{cis}(x) = \cos(x) + i\sin(x),\,</math>		<math display="block">\prod_{k=1}^n \left(2a + 2\cos\left(\frac{2 \pi k m}{n} + x\right)\right) = 2\left( T_n(a)+{(-1)}^{n+m}\cos(n x) \right)</math>
			where {{mvar|T<sub>n</sub>}} is the ].{{citation needed|date=October 2023}}
	i.e. "cis" abbreviates "cos&nbsp;+&nbsp;''i''&nbsp;sin".
			The following relationship holds for the sine function
	"Why", a mathematician may ask, "should one introduce such a notation, rather than writing simply ''e''<sup>''ix''</sup>?".
			<math display="block">\prod_{k=1}^{n-1} \sin\left(\frac{k\pi}{n}\right) = \frac{n}{2^{n-1}}.</math>
	==== Convenience ====
	This notation was more common in the post WWII era when type-writers were used to convey mathematical expressions.
	Superscripts are both offset vertically and smaller than 'cis' or 'exp'; hence, they can be problematic even for hand writing.
	For example ''e''<sup> ''ix''²</sup> versus cis( ''x''²) versus exp( ''ix''²). For many readers, cis( ''x''²) is the clearest, easiest to read of the three. And in fact it is composed of the minimum number of symbols: (3: cis,x,2) compared to (4: e,,i,x,2) and (4: exp,,i,x,2). It is therefore a more compact notation, regardless of the subjective reader.
			More generally for an integer {{math|''n'' > 0}}<ref>{{cite web |title=Product Identity Multiple Angle |url=https://math.stackexchange.com/q/2095330 }}</ref>
	It is also sometimes used to emphasize one method of viewing and dealing with a problem over an other. The mathematics of trigonometry and exponentials are related but not exactly the same. Exponential emphasizes the whole, where as cis and cos&nbsp;+&nbsp;''i''&nbsp;sin notations emphasis the parts. A sort of rhetorical technique for mathematicians, engineers, etc.
			<math display="block">\sin(nx) = 2^{n-1}\prod_{k=0}^{n-1} \sin\left(\frac{k}{n}\pi + x\right) = 2^{n-1}\prod_{k=1}^{n} \sin\left(\frac{k}{n}\pi - x\right).</math>
	It also serves as a mnemonic.
			or written in terms of the ] function <math display=inline>\operatorname{crd}x \equiv 2\sin\tfrac12x</math>,
	==== Pedagogy ====
	In some contexts, this notation may serve the pedagogical purpose of emphasizing that one has not yet proved that this is an exponential function. In doing trigonometry without complex numbers, one may prove the two identities
			<math display="block">\operatorname{crd}(nx) = \prod_{k=1}^{n} \operatorname{crd}\left(\frac{k}{n}2\pi - x\right).</math>
	:<math>\cos(x+y) = \cos(x)\cos(y) - \sin(x)\sin(y) = c_1 c_2 - s_1 s_2,\,</math>
	:<math>\sin(x+y) = \sin(x)\cos(y) + \cos(x)\sin(y) = s_1 c_2 + c_1 s_2.\,</math>
			This comes from the ] <math display=inline>z^n - 1</math> into linear factors (cf. ]): For any complex {{mvar|z}} and an integer {{math|''n'' > 0}},
	Similarly in treating multiplication of complex numbers (with no involvement of trigonometry), one may observe that the real and imaginary parts of the product of ''c''<sub>1</sub>&nbsp;+&nbsp;''is''<sub>1</sub> and ''c''<sub>2</sub>&nbsp;+&nbsp;''is''<sub>2</sub> are respectively
			<math display="block">z^n - 1 = \prod_{k=1}^{n}\left( z - \exp\Bigl(\frac{k}{n}2\pi i\Bigr)\right).</math>
	:<math>c_1 c_2 - s_1 s_2,\,</math>
	:<math>s_1 c_2 + c_1 s_2.\,</math>
			== Linear combinations ==
	Thus one sees this same pattern arising in two disparate contexts:
			For some purposes it is important to know that any linear combination of sine waves of the same period or frequency but different ] is also a sine wave with the same period or frequency, but a different phase shift. This is useful in ] ], because the measured or observed data are linearly related to the {{mvar|a}} and {{mvar|b}} unknowns of the ] basis below, resulting in a simpler ], compared to that of <math>c</math> and <math>\varphi</math>.
			=== Sine and cosine ===
	* trigonometry without complex numbers, and
			The linear combination, or harmonic addition, of sine and cosine waves is equivalent to a single sine wave with a phase shift and scaled amplitude,<ref>Apostol, T.M. (1967) Calculus. 2nd edition. New York, NY, Wiley. Pp 334-335.</ref><ref name="ReferenceB">{{MathWorld|id=HarmonicAdditionTheorem|title=Harmonic Addition Theorem}}</ref>
	* complex numbers without trigonometry.
			<math display="block">a\cos x+b\sin x=c\cos(x+\varphi)</math>
	This coincidence can serve as a motivation for conjoining the two contexts and thereby discovering the trigonometric identity
			where <math>c</math> and <math>\varphi</math> are defined as so:
	:<math>\operatorname{cis}(x+y) = \operatorname{cis}(x)\operatorname{cis}(y),\,</math>
			<math display="block">\begin{align}
	and observing that this identity for cis of a sum is simpler than the identities for sin and cos of a sum. Having proved this identity, one can challenge the students to recall which familiar sort of function satisfies this same ]
			c &= \sgn(a) \sqrt{a^2 + b^2}, \\
			\varphi &= {\arctan}\bigl({-b/a}\bigr),
			\end{align}</math>
	:<math>f(x+y) = f(x)f(y).\,</math>		given that <math>a \neq 0.</math>
			=== Arbitrary phase shift ===
	The answer is ]s. That suggests that cis may be an exponential function
			More generally, for arbitrary phase shifts, we have
	:<math>\operatorname{cis}(x) = b^x.\,</math>		<math display="block">a \sin(x + \theta_a) + b \sin(x + \theta_b)= c \sin(x+\varphi)</math>
			where <math>c</math> and <math>\varphi</math> satisfy:
	Then the question is: what is the base ''b''? The definition of cis and the local behavior of sin and cos near zero suggest that
			<math display="block">\begin{align}
	:<math>\operatorname{cis}(0+dx) = \operatorname{cis}(0) + i\,dx,</math>
			c^2 &= a^2 + b^2 + 2ab\cos \left(\theta_a - \theta_b \right) , \\
			\tan \varphi &= \frac{a \sin \theta_a + b \sin \theta_b}{a \cos \theta_a + b \cos \theta_b}.
			\end{align}</math>
			=== More than two sinusoids ===
	(where ''dx'' is an ] increment of ''x''). Thus the rate of change at 0 is ''i'', so the base should be ''e''<sup>''i''</sup>. Thus if this is an exponential function, then it must be
			{{See also|phasor (sine waves)#Addition|label1=Phasor addition}}The general case reads<ref name="ReferenceB" />
			<math display="block">\sum_i a_i \sin(x + \theta_i) = a \sin(x + \theta),</math>
			where
			<math display="block">a^2 = \sum_{i,j}a_i a_j \cos(\theta_i - \theta_j)</math>
			and
			<math display="block">\tan\theta = \frac{\sum_i a_i \sin\theta_i}{\sum_i a_i \cos\theta_i}.</math>
			== Lagrange's trigonometric identities ==
	:<math>\operatorname{cis}(x) = e^{ix}.\,</math>
			These identities, named after ], are:<ref name=Muniz>{{cite journal |first=Eddie |last=Ortiz Muñiz |date=Feb 1953 |volume=21 |number=2 |title=A Method for Deriving Various Formulas in Electrostatics and Electromagnetism Using Lagrange's Trigonometric Identities |journal=American Journal of Physics |page=140 | doi=10.1119/1.1933371 | bibcode=1953AmJPh..21..140M }}</ref><ref>{{cite book |title=Ordinary and Partial Differential Equations: With Special Functions, Fourier Series, and Boundary Value Problems | edition=illustrated |first1=Ravi P. |last1=Agarwal |first2=Donal |last2=O'Regan |publisher=Springer Science & Business Media |year=2008 |isbn=978-0-387-79146-3 |page=185 |url=https://books.google.com/books?id=jWvAfcNnphIC}} </ref><ref>{{cite book |title=Handbook of Mathematical Formulas and Integrals |edition=4th |first1=Alan |last1=Jeffrey |first2=Hui-hui |last2=Dai |chapter=Section 2.4.1.6 |isbn=978-0-12-374288-9 |year=2008 |publisher=Academic Press}}</ref>
			<math display="block">\begin{align}
			\sum_{k=0}^n \sin k\theta & = \frac{\cos \tfrac12\theta - \cos\left(\left(n + \tfrac12\right)\theta\right)}{2\sin\tfrac12\theta}\\
			\sum_{k=0}^n \cos k\theta & = \frac{\sin \tfrac12\theta + \sin\left(\left(n + \tfrac12\right)\theta\right)}{2\sin\tfrac12\theta}
			\end{align}</math>
			for <math>\theta \not\equiv 0 \pmod{2\pi}.</math>
			A related function is the ]:
	==Infinite product formula==
	For applications to ]s, the following ] formulæ for trigonometric functions are useful:
	{{col-start}}
	{{col-2}}
	: <math>\sin x = x \prod_{n = 1}^\infty\left(1 - \frac{x^2}{\pi^2 n^2}\right)</math>
	: <math>\sinh x = x \prod_{n = 1}^\infty\left(1 + \frac{x^2}{\pi^2 n^2}\right)</math>		<math display="block">D_n(\theta) = 1 + 2\sum_{k=1}^n \cos k\theta
			= \frac{\sin\left(\left(n + \tfrac12 \right)\theta\right)}{\sin \tfrac12 \theta}.</math>
			A similar identity is<ref>{{Cite journal |last=Fay |first=Temple H. |last2=Kloppers |first2=P. Hendrik |date=2001 |title=The Gibbs' phenomenon |url=http://dx.doi.org/10.1080/00207390117151 |journal=International Journal of Mathematical Education in Science and Technology |volume=32 |issue=1 |pages=73–89 |doi=10.1080/00207390117151}}</ref>
	: <math>\frac{\sin x}{x} = \prod_{n = 1}^\infty\cos\left(\frac{x}{2^n}\right)</math>
	{{col-2}}
	: <math>\cos x = \prod_{n = 1}^\infty\left(1 - \frac{x^2}{\pi^2(n - \frac{1}{2})^2}\right)</math>
	: <math>\cosh x = \prod_{n = 1}^\infty\left(1 + \frac{x^2}{\pi^2(n - \frac{1}{2})^2}\right)</math>		<math display="block">\sum_{k=1}^n \cos (2k -1)\alpha = \frac{\sin (2n \alpha)}{2 \sin \alpha}.</math>
	{{col-end}}
			The proof is the following. By using the ],
	==The Gudermannian function==
			<math display="block">\sin (A + B) - \sin (A - B) = 2 \cos A \sin B.</math>
	The ] relates the ] and ] trigonometric functions without resorting to ]; see that article for details.
			Then let's examine the following formula,
			<math display="block">2 \sin \alpha \sum_{k=1}^n \cos (2k - 1)\alpha = 2\sin \alpha \cos \alpha + 2 \sin \alpha \cos 3\alpha
	==Identities without variables==
			+ 2 \sin \alpha \cos 5 \alpha + \ldots + 2 \sin \alpha \cos (2n - 1) \alpha </math>
	The ]
			and this formula can be written by using the above identity,
			<math display="block">\begin{align}
	:<math>\cos 20^\circ\cdot\cos 40^\circ\cdot\cos 80^\circ=\frac{1}{8}</math>
			& 2 \sin \alpha \sum_{k=1}^n \cos (2k - 1)\alpha \\
	is a special case of an identity that contains one variable:
			&\quad= \sum_{k=1}^n (\sin (2k \alpha) - \sin (2(k - 1)\alpha)) \\
			&\quad= (\sin 2\alpha - \sin 0) + (\sin 4 \alpha - \sin 2 \alpha) + (\sin 6 \alpha - \sin 4 \alpha) + \ldots
			+ (\sin (2n \alpha) - \sin (2(n - 1) \alpha)) \\
			&\quad= \sin (2n \alpha).
			\end{align}</math>
			So, dividing this formula with <math>2 \sin \alpha</math> completes the proof.
	:<math>\prod_{j=0}^{k-1}\cos(2^j x)=\frac{\sin(2^k x)}{2^k\sin(x)}.</math>
			== Certain linear fractional transformations ==
	A similar-looking identity is
			If <math>f(x)</math> is given by the ]
			<math display="block">f(x) = \frac{(\cos\alpha)x - \sin\alpha}{(\sin\alpha)x + \cos\alpha},</math>
			and similarly
			<math display="block">g(x) = \frac{(\cos\beta)x - \sin\beta}{(\sin\beta)x + \cos\beta},</math>
			then
			<math display="block">f\big(g(x)\big) = g\big(f(x)\big)
			= \frac{\big(\cos(\alpha+\beta)\big)x - \sin(\alpha+\beta)}{\big(\sin(\alpha+\beta)\big)x + \cos(\alpha+\beta)}.</math>
			More tersely stated, if for all <math>\alpha</math> we let <math>f_{\alpha}</math> be what we called <math>f</math> above, then
	:<math> \cos\frac{\pi}{7}\cos\frac{2\pi}{7}\cos\frac{3\pi}{7} = \frac{1}{8}, </math>
			<math display="block">f_\alpha \circ f_\beta = f_{\alpha+\beta}.</math>
			If <math>x</math> is the slope of a line, then <math>f(x)</math> is the slope of its rotation through an angle of <math>- \alpha.</math>
	and in addition
			== Relation to the complex exponential function ==
	:<math>\sin 20^\circ\cdot\sin 40^\circ\cdot\sin 80^\circ=\sqrt{3}/8.</math>
			{{Main|Euler's formula}}
			Euler's formula states that, for any real number ''x'':<ref>Abramowitz and Stegun, p.&nbsp;74, 4.3.47</ref>
	The following is perhaps not as readily generalized to an identity containing variables:
			<math display="block">e^{ix} = \cos x + i\sin x,</math>
			where ''i'' is the ]. Substituting −''x'' for ''x'' gives us:
			<math display="block">e^{-ix} = \cos(-x) + i\sin(-x) = \cos x - i\sin x.</math>
			These two equations can be used to solve for cosine and sine in terms of the ]. Specifically,<ref>Abramowitz and Stegun, p.&nbsp;71, 4.3.2</ref><ref>Abramowitz and Stegun, p.&nbsp;71, 4.3.1</ref>
	:<math>\cos 24^\circ+\cos 48^\circ+\cos 96^\circ+\cos 168^\circ=\frac{1}{2}.</math>
			<math display="block">\cos x = \frac{e^{ix} + e^{-ix}}{2}</math>
			<math display="block">\sin x = \frac{e^{ix} - e^{-ix}}{2i}</math>
			These formulae are useful for proving many other trigonometric identities. For example, that
	Degree measure ceases to be more felicitous than radian measure when we consider this identity with 21 in the denominators:
			{{math|1=''e''<sup>''i''(''θ''+''φ'')</sup> = ''e''<sup>''iθ''</sup> ''e''<sup>''iφ''</sup>}} means that
	:<math> \cos\left( \frac{2\pi}{21}\right)
			{{block indent|em=1.5|text={{math|1=cos(''θ'' + ''φ'') + ''i'' sin(''θ'' + ''φ'') = (cos ''θ'' + ''i'' sin ''θ'') (cos ''φ'' + ''i'' sin ''φ'') = (cos ''θ'' cos ''φ'' − sin ''θ'' sin ''φ'') + ''i'' (cos ''θ'' sin ''φ'' + sin ''θ'' cos ''φ'')}}.}}
	\,+\, \cos\left(2\cdot\frac{2\pi}{21}\right)
			That the real part of the left hand side equals the real part of the right hand side is an angle addition formula for cosine. The equality of the imaginary parts gives an angle addition formula for sine.
	\,+\, \cos\left(4\cdot\frac{2\pi}{21}\right)</math>
	::<math>
	\,+\, \cos\left( 5\cdot\frac{2\pi}{21}\right)
	\,+\, \cos\left( 8\cdot\frac{2\pi}{21}\right)
	\,+\, \cos\left(10\cdot\frac{2\pi}{21}\right)=\frac{1}{2}.</math>
			The following table expresses the trigonometric functions and their inverses in terms of the exponential function and the ].
	The factors 1, 2, 4, 5, 8, 10&nbsp;may start to make the pattern clear: they are those integers less than 21/2 that are ] to (or have no ]s in common with) 21. The last several examples are corollaries of a basic fact about the irreducible ]s: the cosines are the real parts of the zeroes of those polynomials; the sum of the zeroes is the ] evaluated at (in the very last case above) 21; only half of the zeroes are present above. The two identities preceding this last one arise in the same fashion with 21 replaced by 10 and 15, respectively.
			{| class="wikitable" style="background-color:var(--background-color-base)"
	An efficient way to ] is based on the following identity without variables, due to ]:
			!Function
			!Inverse function<ref>Abramowitz and Stegun, p.&nbsp;80, 4.4.26–31</ref>
			|-
			|<math>\sin \theta = \frac{e^{i\theta} - e^{-i\theta}}{2i}</math>
			|<math>\arcsin x = -i\, \ln \left(ix + \sqrt{1 - x^2}\right)</math>
			|-
			|<math>\cos \theta = \frac{e^{i\theta} + e^{-i\theta}}{2}</math>
			|<math>\arccos x = -i\ln\left(x+\sqrt{x^2-1}\right)</math>
			|-
			|<math>\tan \theta = -i\, \frac{e^{i\theta} - e^{-i\theta}}{e^{i\theta} + e^{-i\theta}}</math>
			|<math>\arctan x = \frac{i}{2} \ln \left(\frac{i + x}{i - x}\right)</math>
			|-
			|<math>\csc \theta = \frac{2i}{e^{i\theta} - e^{-i\theta}}</math>
			|<math>\arccsc x = -i\, \ln \left(\frac{i}{x} + \sqrt{1 - \frac{1}{x^2}}\right)</math>
			|-
			|<math>\sec \theta = \frac{2}{e^{i\theta} + e^{-i\theta}}</math>
			|<math>\arcsec x = -i\, \ln \left(\frac{1}{x} +i \sqrt{1 - \frac{1}{x^2}}\right)</math>
			|-
			|<math>\cot \theta = i\, \frac{e^{i\theta} + e^{-i\theta}}{e^{i\theta} - e^{-i\theta}}</math>
			|<math>\arccot x = \frac{i}{2} \ln \left(\frac{x - i}{x + i}\right)</math>
			|-
			|]
			|<math>\operatorname{arccis} x = -i \ln x</math>
			|}
			== Relation to complex hyperbolic functions ==
	:<math>\frac{\pi}{4} = 4 \arctan\frac{1}{5} - \arctan\frac{1}{239}</math>
			Trigonometric functions may be deduced from ] with ] arguments. The formulae for the relations are shown below<ref>{{Cite book |last=Hawkins |first=Faith Mary |url=https://archive.org/details/isbn_356025055/mode/2up |title=Complex Numbers and Elementary Complex Functions |last2=Hawkins |first2=J. Q. |date=March 1, 1969 |publisher=MacDonald Technical & Scientific London |year=1969 |isbn=978-0356025056 |location=London |publication-date=1968 |pages=122 |language=english}}</ref><ref>{{Cite book |last=Markushevich |first=A. I. |url=https://archive.org/details/markushevich-the-remarkable-sine-functions |title=The Remarkable Sine Function |publisher=American Elsevier Publishing Company, Inc. |year=1966 |isbn=978-1483256313 |location=New York |publication-date=1966 |pages=35-37, 81 |language=english}}</ref>.<math display="block">\begin{align}
			\sin x &= -i \sinh (ix) \\
			\cos x &= \cosh (ix) \\
			\tan x &= -i \tanh (i x) \\
			\cot x &= i \coth (i x) \\
			\sec x &= \operatorname{sech} (i x) \\
			\csc x &= i \operatorname{csch} (i x) \\
			\end{align}</math>
			== Series expansion ==
	or, alternatively, by using ]'s formula:
			When using a ] expansion to define trigonometric functions, the following identities are obtained:<ref>Abramowitz and Stegun, p.&nbsp;74, 4.3.65–66</ref>
			:<math display="block">\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots = \sum_{n=0}^{\infty} \frac{(-1)^nx^{2n+1}}{(2n+1)!},</math><math display="block">\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots = \sum_{n=0}^{\infty} \frac{(-1)^nx^{2n}}{(2n)!}.</math>
			== Infinite product formulae ==
	:<math>\frac{\pi}{4} = 5 \arctan\frac{1}{7} + 2 \arctan\frac{3}{79}.</math>
			For applications to ], the following ] formulae for trigonometric functions are useful:<ref>Abramowitz and Stegun, p.&nbsp;75, 4.3.89–90</ref><ref>Abramowitz and Stegun, p.&nbsp;85, 4.5.68–69</ref>
			<math display=block>\begin{align}
	<!-- extra blank space between two TeX displays for legibility -->
			\sin x &= x \prod_{n = 1}^\infty\left(1 - \frac{x^2}{\pi^2 n^2}\right), &
			\cos x &= \prod_{n = 1}^\infty\left(1 - \frac{x^2}{\pi^2\left(n - \frac{1}{2}\right)\!\vphantom)^2}\right), \\
			\sinh x &= x \prod_{n = 1}^\infty\left(1 + \frac{x^2}{\pi^2 n^2}\right), &
			\cosh x &= \prod_{n = 1}^\infty\left(1 + \frac{x^2}{\pi^2\left(n - \frac{1}{2}\right)\!\vphantom)^2}\right).
			\end{align}</math>
			== Inverse trigonometric functions ==
	:<math>
			{{Main|Inverse trigonometric functions}}
	\begin{matrix}
	\sin 0 & = & \sin 0^\circ &; = & 0 & = & \cos 90^\circ & = & \cos \left( \frac {\pi} {2} \right) \\ \\
			The following identities give the result of composing a trigonometric function with an inverse trigonometric function.<ref>{{harvnb|Abramowitz|Stegun|1972|loc=p. 73, 4.3.45}}</ref>
	\sin \left( \frac {\pi} {6} \right) & = & \sin 30^\circ & = & 1/2 & = & \cos 60^\circ & = & \cos \left( \frac {\pi} {3} \right) \\ \\
	\sin \left( \frac {\pi} {4} \right) & = & \sin 45^\circ & = & \sqrt{2}/2 & = & \cos 45^\circ & = & \cos \left( \frac {\pi} {4} \right) \\ \\
			<math display=block>
	\sin \left( \frac {\pi} {3} \right) & = & \sin 60^\circ & = & \sqrt{3}/2 & = & \cos 30^\circ & = & \cos \left( \frac {\pi} {6} \right) \\ \\
			\begin{align}
	\sin \left( \frac {\pi} {2} \right) & = & \sin 90^\circ & = & 1 & = & \cos 0^\circ & = & \cos 0
			\sin(\arcsin x) &=x
	\end{matrix}
			& \cos(\arcsin x) &=\sqrt{1-x^2}
			& \tan(\arcsin x) &=\frac{x}{\sqrt{1 - x^2}}
			\\
			\sin(\arccos x) &=\sqrt{1-x^2}
			& \cos(\arccos x) &=x
			& \tan(\arccos x) &=\frac{\sqrt{1 - x^2}}{x}
			\\
			\sin(\arctan x) &=\frac{x}{\sqrt{1+x^2}}
			& \cos(\arctan x) &=\frac{1}{\sqrt{1+x^2}}
			& \tan(\arctan x) &=x
			\\
			\sin(\arccsc x) &=\frac{1}{x}
			& \cos(\arccsc x) &=\frac{\sqrt{x^2 - 1}}{x}
			& \tan(\arccsc x) &=\frac{1}{\sqrt{x^2 - 1}}
			\\
			\sin(\arcsec x) &=\frac{\sqrt{x^2 - 1}}{x}
			& \cos(\arcsec x) &=\frac{1}{x}
			& \tan(\arcsec x) &=\sqrt{x^2 - 1}
			\\
			\sin(\arccot x) &=\frac{1}{\sqrt{1+x^2}}
			& \cos(\arccot x) &=\frac{x}{\sqrt{1+x^2}}
			& \tan(\arccot x) &=\frac{1}{x}
			\\
			\end{align}
	</math>		</math>
			Taking the ] of both sides of the each equation above results in the equations for <math>\csc = \frac{1}{\sin}, \;\sec = \frac{1}{\cos}, \text{ and } \cot = \frac{1}{\tan}.</math>
	:<math>\sin{\frac{\pi}{7}}=\frac{\sqrt{7}}{6}-
			The right hand side of the formula above will always be flipped.
	\frac{\sqrt{7}}{189} \sum_{j=0}^{\infty} \frac{(3j+1)!}{189^j j!\,(2j+2)!}
			For example, the equation for <math>\cot(\arcsin x)</math> is:
	\!</math>
			<math display=block>\cot(\arcsin x) = \frac{1}{\tan(\arcsin x)} = \frac{1}{\frac{x}{\sqrt{1 - x^2}}} = \frac{\sqrt{1 - x^2}}{x}</math>
			while the equations for <math>\csc(\arccos x)</math> and <math>\sec(\arccos x)</math> are:
			<math display=block>\csc(\arccos x) = \frac{1}{\sin(\arccos x)} = \frac{1}{\sqrt{1-x^2}} \qquad \text{ and }\quad \sec(\arccos x) = \frac{1}{\cos(\arccos x)} = \frac{1}{x}.</math>
			The following identities are implied by the ]. They hold whenever <math>x, r, s, -x, -r, \text{ and } -s</math> are in the domains of the relevant functions.
	:<math>\sin{\frac{\pi}{18}}=
			<math display=block>\begin{alignat}{9}
	\frac{1}{6} \sum_{j=0}^{\infty} \frac{(3j)!}{27^j j!\,(2j+1)!}
			\frac{\pi}{2} ~&=~ \arcsin(x) &&+ \arccos(x) ~&&=~ \arctan(r) &&+ \arccot(r) ~&&=~ \arcsec(s) &&+ \arccsc(s) \\
	\!</math>
			\pi ~&=~ \arccos(x) &&+ \arccos(-x) ~&&=~ \arccot(r) &&+ \arccot(-r) ~&&=~ \arcsec(s) &&+ \arcsec(-s) \\
			0 ~&=~ \arcsin(x) &&+ \arcsin(-x) ~&&=~ \arctan(r) &&+ \arctan(-r) ~&&=~ \arccsc(s) &&+ \arccsc(-s) \\
			\end{alignat}</math>
			Also,<ref name=Wu>Wu, Rex H. "Proof Without Words: Euler's Arctangent Identity", ''Mathematics Magazine'' 77(3), June 2004, p. 189.</ref>
	With the ] φ:
			<math display=block>\begin{align}
			\arctan x + \arctan \dfrac{1}{x}
			&= \begin{cases}
			\frac{\pi}{2}, & \text{if } x > 0 \\
			- \frac{\pi}{2}, & \text{if } x < 0
			\end{cases} \\
			\arccot x + \arccot \dfrac{1}{x}
			&= \begin{cases}
			\frac{\pi}{2}, & \text{if } x > 0 \\
			\frac{3\pi}{2}, & \text{if } x < 0
			\end{cases} \\
			\end{align}</math>
			<math display=block>\arccos \frac{1}{x} = \arcsec x \qquad \text{ and } \qquad \arcsec \frac{1}{x} = \arccos x</math>
			<math display=block>\arcsin \frac{1}{x} = \arccsc x \qquad \text{ and } \qquad \arccsc \frac{1}{x} = \arcsin x</math>
			The ] function can be expanded as a series:<ref>{{citation | title = Algorithmic determination of a large integer in the two-term Machin-like formula for π | journal = Mathematics | author = S. M. Abrarov, R. K. Jagpal, R. Siddiqui and B. M. Quine | doi = 10.3390/math9172162 | year = 2021 | volume = 9 | issue = 17 | at = 2162| doi-access = free | arxiv = 2107.01027 }}</ref>
	:<math>\cos \left( \frac {\pi} {5} \right) = \cos 36^\circ={\sqrt{5}+1 \over 4} = \varphi /2
			<math display=block>
			\arctan(nx) = \sum_{m = 1}^n \arctan\frac{x}{1 + (m - 1)mx^2}
	</math>		</math>
			== Identities without variables ==
	:<math>\sin \left( \frac {\pi} {10} \right) = \sin 18^\circ = {\sqrt{5}-1 \over 4} = {\varphi - 1 \over 2} = {1 \over 2\varphi}</math>
			In terms of the ] function we have<ref name="Wu" />
	Also see ].
			<math display="block">\arctan \frac{1}{2} = \arctan \frac{1}{3} + \arctan \frac{1}{7}.</math>
			The curious identity known as ],
	==Calculus==
			<math display="block">\cos 20^\circ\cdot\cos 40^\circ\cdot\cos 80^\circ = \frac{1}{8},</math>
	In ] the relations stated below require angles to be measured in ]s; the relations would become more complicated if angles were measured in another unit such as degrees. If the trigonometric functions are defined in terms of geometry, their derivatives can be found by verifying two limits. The first is:
			is a special case of an identity that contains one variable:
	:<math>\lim_{x\rightarrow 0}\frac{\sin(x)}{x}=1,</math>
			<math display="block">\prod_{j=0}^{k-1}\cos\left(2^j x\right) = \frac{\sin\left(2^k x\right)}{2^k\sin x}.</math>
			Similarly,
	verified using the ] and ]. It may be tempting to propose to use ] to establish this limit. However, if one uses this limit in order to prove that the derivative of the sine is the cosine, and then uses the fact that the derivative of the sine is the cosine in applying L'Hôpital's rule, one is reasoning circularly&mdash;a logical fallacy. The second limit is:
			<math display="block">\sin 20^\circ\cdot\sin 40^\circ\cdot\sin 80^\circ = \frac{\sqrt{3}}{8}</math>
			is a special case of an identity with <math>x = 20^\circ</math>:
			<math display="block">\sin x \cdot \sin \left(60^\circ - x\right) \cdot \sin \left(60^\circ + x\right) = \frac{\sin 3x}{4}.</math>
	:<math>\lim_{x\rightarrow 0}\frac{1-\cos(x)}{x}=0,</math>		For the case <math>x = 15^\circ</math>,
			<math display="block">\begin{align}
			\sin 15^\circ\cdot\sin 45^\circ\cdot\sin 75^\circ &= \frac{\sqrt{2}}{8}, \\
			\sin 15^\circ\cdot\sin 75^\circ &= \frac{1}{4}.
			\end{align}</math>
			For the case <math>x = 10^\circ</math>,
	verified using the identity tan(''x''/2)&nbsp;=&nbsp;(1&nbsp;&minus;&nbsp;cos(''x''))/sin(''x''). Having established these two limits, one can use the limit definition of the derivative and the addition theorems to show that sin&prime;(''x'')&nbsp;=&nbsp;cos(''x'') and cos&prime;(''x'')&nbsp;=&nbsp;&minus;sin(''x''). If the sine and cosine functions are defined by their ], then the derivatives can be found by differentiating the power series term-by-term.
			<math display="block">\sin 10^\circ\cdot\sin 50^\circ\cdot\sin 70^\circ = \frac{1}{8}.</math>
			The same cosine identity is
	:<math>{d \over dx}\sin(x) = \cos(x)</math>
			<math display="block">\cos x \cdot \cos \left(60^\circ - x\right) \cdot \cos \left(60^\circ + x\right) = \frac{\cos 3x}{4}.</math>
			Similarly,
	The rest of the trigonometric functions can be differentiated using the above identities and the rules of ]:
			<math display="block">\begin{align}
			\cos 10^\circ\cdot\cos 50^\circ\cdot\cos 70^\circ &= \frac{\sqrt{3}}{8}, \\
			\cos 15^\circ\cdot\cos 45^\circ\cdot\cos 75^\circ &= \frac{\sqrt{2}}{8}, \\
			\cos 15^\circ\cdot\cos 75^\circ &= \frac{1}{4}.
			\end{align}</math>
			Similarly,
	:<math>
	\begin{matrix}		<math display="block">\begin{align}
			\tan 50^\circ\cdot\tan 60^\circ\cdot\tan 70^\circ &= \tan 80^\circ, \\
	{d \over dx} \sin x =& \cos x ,& {d \over dx} \arcsin x =& {1 \over \sqrt{1 - x^2} } \\ \\
			\tan 40^\circ\cdot\tan 30^\circ\cdot\tan 20^\circ &= \tan 10^\circ.
	{d \over dx} \cos x =& -\sin x ,& {d \over dx} \arccos x =& {-1 \over \sqrt{1 - x^2}} \\ \\
			\end{align}</math>
	{d \over dx} \tan x =& \sec^2 x ,& {d \over dx} \arctan x =& { 1 \over 1 + x^2} \\ \\
	{d \over dx} \cot x =& -\csc^2 x ,& {d \over dx} \arccot x =& {-1 \over 1 + x^2} \\ \\
	{d \over dx} \sec x =& \tan x \sec x ,& {d \over dx} \arcsec x =& { 1 \over |x|\sqrt{x^2 - 1}} \\ \\
	{d \over dx} \csc x =& -\csc x \cot x ,& {d \over dx} \arccsc x =& {-1 \over |x|\sqrt{x^2 - 1}}
	\end{matrix}
	</math>
			The following is perhaps not as readily generalized to an identity containing variables (but see explanation below):
	The integral identities can be found in "]".
			<math display="block">\cos 24^\circ + \cos 48^\circ + \cos 96^\circ + \cos 168^\circ = \frac{1}{2}.</math>
			Degree measure ceases to be more felicitous than radian measure when we consider this identity with 21 in the denominators:
	===Implications===
			<math display="block">
	The fact that the differentiation of trigonometric functions (sine and cosine) results in ]s of the same two functions is of fundamental importance to many fields of mathematics, including ] and ]ations.
			\cos \frac{2\pi}{21} +
			\cos\left(2\cdot\frac{2\pi}{21}\right) +
			\cos\left(4\cdot\frac{2\pi}{21}\right) +
			\cos\left( 5\cdot\frac{2\pi}{21}\right) +
			\cos\left( 8\cdot\frac{2\pi}{21}\right) +
			\cos\left(10\cdot\frac{2\pi}{21}\right)
			= \frac{1}{2}.</math>
			The factors 1, 2, 4, 5, 8, 10&nbsp;may start to make the pattern clear: they are those integers less than {{sfrac|21|2}} that are ] to (or have no ]s in common with) 21. The last several examples are corollaries of a basic fact about the irreducible ]s: the cosines are the real parts of the zeroes of those polynomials; the sum of the zeroes is the ] evaluated at (in the very last case above) 21; only half of the zeroes are present above. The two identities preceding this last one arise in the same fashion with 21 replaced by 10 and 15, respectively.
	== Exponential definitions ==
	{| class="wikitable" style="background-color:#FFFFFF"
	!Function
	!Inverse Function
			Other cosine identities include:<ref>{{cite journal|last=Humble |first=Steve |title=Grandma's identity |journal=Mathematical Gazette |volume=88 |date=Nov 2004 |pages=524–525 |doi=10.1017/s0025557200176223|s2cid=125105552 }}</ref>
	|-
			<math display="block">\begin{align}
	|<math>\sin \theta = \frac{e^{i\theta} - e^{-i\theta}}{2i} \,</math>
			2\cos \frac{\pi}{3} &= 1, \\
	|<math>\arcsin x = -i \ln \left(ix + \sqrt{1 - x^2}\right) \,</math>
			2\cos \frac{\pi}{5} \times 2\cos \frac{2\pi}{5} &= 1, \\
			2\cos \frac{\pi}{7} \times 2\cos \frac{2\pi}{7}\times 2\cos \frac{3\pi}{7} &= 1,
			\end{align}</math>
			and so forth for all odd numbers, and hence
			<math display="block">\cos \frac{\pi}{3}+\cos \frac{\pi}{5} \times \cos \frac{2\pi}{5} + \cos \frac{\pi}{7} \times \cos \frac{2\pi}{7} \times \cos \frac{3\pi}{7} + \dots = 1.</math>
			Many of those curious identities stem from more general facts like the following:<ref>{{MathWorld|id=Sine|title=Sine}}</ref>
	|-
	|<math>\cos \theta = \frac{e^{i\theta} + e^{-i\theta}}{2} \,</math>		<math display="block">\prod_{k=1}^{n-1} \sin\frac{k\pi}{n} = \frac{n}{2^{n-1}}</math>
			and
	|<math>\arccos x = -i \ln \left(x + \sqrt{x^2 - 1}\right) \,</math>
			<math display="block">\prod_{k=1}^{n-1} \cos\frac{k\pi}{n} = \frac{\sin\frac{\pi n}{2}}{2^{n-1}}.</math>
			Combining these gives us
	|-
	|<math>\tan \theta = \frac{e^{i\theta} - e^{-i\theta}}{i(e^{i\theta} + e^{-i\theta})} \,</math>		<math display="block">\prod_{k=1}^{n-1} \tan\frac{k\pi}{n} = \frac{n}{\sin\frac{\pi n}{2}}</math>
	|<math>\arctan x = \frac{i \ln \left(\frac{i + x}{i - x}\right)}{2} \,</math>
			If {{mvar|n}} is an odd number (<math>n = 2 m + 1</math>) we can make use of the symmetries to get
	|-
	|<math>\csc \theta = \frac{2i}{e^{i\theta} - e^{-i\theta}} \,</math>		<math display="block">\prod_{k=1}^{m} \tan\frac{k\pi}{2m+1} = \sqrt{2m+1}</math>
	|<math>\arccsc x = -i \ln \left(\tfrac{i}{x} + \sqrt{1 - \tfrac{1}{x^2}}\right) \,</math>
			The transfer function of the ] can be expressed in terms of polynomial and poles. By setting the frequency as the cutoff frequency, the following identity can be proved:
	|-
			<math display="block">\prod_{k=1}^n \sin\frac{\left(2k - 1\right)\pi}{4n} = \prod_{k=1}^{n} \cos\frac{\left(2k-1\right)\pi}{4n} = \frac{\sqrt{2}}{2^n}</math>
	|<math>\sec \theta = \frac{2}{e^{i\theta} + e^{-i\theta}} \,</math>
	|<math>\arcsec x = -i \ln \left(\tfrac{1}{x} + \sqrt{1 - \tfrac{i}{x^2}}\right) \,</math>
			=== Computing {{pi}} ===
	|-
			An efficient way to ] to a ] is based on the following identity without variables, due to ]. This is known as a ]:
	|<math>\cot \theta = \frac{i(e^{i\theta} + e^{-i\theta})}{e^{i\theta} - e^{-i\theta}} \,</math>
	|<math>\arccot x = \frac{i \ln \left(\frac{i - x}{i + x}\right)}{2} \,</math>		<math display="block">\frac{\pi}{4} = 4 \arctan\frac{1}{5} - \arctan\frac{1}{239}</math>
			or, alternatively, by using an identity of ]:
	|-
			<math display="block">\frac{\pi}{4} = 5 \arctan\frac{1}{7} + 2 \arctan\frac{3}{79}</math>
	!
			or by using ]s:
	!
			<math display="block">\pi = \arccos\frac{4}{5} + \arccos\frac{5}{13} + \arccos\frac{16}{65} = \arcsin\frac{3}{5} + \arcsin\frac{12}{13} + \arcsin\frac{63}{65}.</math>
	|-
	|<math>\operatorname{cis} \, \theta = e^{i\theta} \,</math>
	|<math>\operatorname{arccis} \, x = \frac{\ln x}{i} \,</math>
	|}
			Others include:<ref name=Harris>Harris, Edward M. "Sums of Arctangents", in Roger B. Nelson, ''Proofs Without Words'' (1993, Mathematical Association of America), p. 39.</ref><ref name="Wu" />
	==Miscellaneous==<!--This section will hopefully be sorted back into the article, If I can work out a place the the stuff to go-->
			<math display="block">\frac{\pi}{4} = \arctan\frac{1}{2} + \arctan\frac{1}{3},</math>
	===Dirichlet kernel===
			<math display="block">\pi = \arctan 1 + \arctan 2 + \arctan 3,</math>
	The ''']''' ''D<sub>n</sub>''(''x'') is the function occurring on both sides of the next identity:
			<math display="block">\frac{\pi}{4} = 2\arctan \frac{1}{3} + \arctan \frac{1}{7}.</math>
			Generally, for numbers {{math|''t''<sub>1</sub>, ..., ''t''<sub>''n''−1</sub> ∈ (−1, 1)}} for which {{math|1=''θ''<sub>''n''</sub> = Σ{{su|b=''k''=1|p=''n''−1}} arctan ''t''<sub>''k''</sub> ∈ (''π''/4, 3''π''/4)}}, let {{math|1=''t''<sub>''n''</sub> = tan(''π''/2 − ''θ''<sub>''n''</sub>) = cot ''θ''<sub>''n''</sub>}}. This last expression can be computed directly using the formula for the cotangent of a sum of angles whose tangents are {{math|''t''<sub>1</sub>, ..., ''t''<sub>''n''−1</sub>}} and its value will be in {{math|(−1, 1)}}. In particular, the computed {{math|''t''<sub>''n''</sub>}} will be rational whenever all the {{math|''t''<sub>1</sub>, ..., ''t''<sub>''n''−1</sub>}} values are rational. With these values,
	:<math>1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots+2\cos(nx) = \frac{ \sin\left(\left(n+\frac{1}{2}\right)x\right) }{ \sin(x/2) }. </math>
			<math display="block">\begin{align}
			\frac{\pi}{2} & = \sum_{k=1}^n \arctan(t_k) \\
			\pi & = \sum_{k=1}^n \sgn(t_k) \arccos\left(\frac{1 - t_k^2}{1 + t_k^2}\right) \\
			\pi & = \sum_{k=1}^n \arcsin\left(\frac{2t_k}{1 + t_k^2}\right) \\
			\pi & = \sum_{k=1}^n \arctan\left(\frac{2t_k}{1 - t_k^2}\right)\,,
			\end{align}</math>
			where in all but the first expression, we have used tangent half-angle formulae. The first two formulae work even if one or more of the {{math|''t''<sub>''k''</sub>}} values is not within {{math|(−1, 1)}}. Note that if {{math|1=''t'' = ''p''/''q''}} is rational, then the {{math|(2''t'', 1 − ''t''<sup>2</sup>, 1 + ''t''<sup>2</sup>)}} values in the above formulae are proportional to the Pythagorean triple {{math|(2''pq'', ''q''<sup>2</sup> − ''p''<sup>2</sup>, ''q''<sup>2</sup> + ''p''<sup>2</sup>)}}.
	The ] of any ] of period 2π with the Dirichlet kernel coincides with the function's ''n''th-degree Fourier approximation. The same holds for any ] or ].
	===Extension of half-angle formulae===
			For example, for {{math|1=''n'' = 3}} terms,
	If we set
			<math display="block">\frac{\pi}{2} = \arctan\left(\frac{a}{b}\right) + \arctan\left(\frac{c}{d}\right) + \arctan\left(\frac{bd - ac}{ad + bc}\right)</math>
			for any {{math|''a'', ''b'', ''c'', ''d'' > 0}}.
			=== An identity of Euclid ===
	:<math>t = \tan\left(\frac{x}{2}\right),</math>
			] showed in Book XIII, Proposition 10 of his '']'' that the area of the square on the side of a regular pentagon inscribed in a circle is equal to the sum of the areas of the squares on the sides of the regular hexagon and the regular decagon inscribed in the same circle. In the language of modern trigonometry, this says:
			<math display="block">\sin^2 18^\circ + \sin^2 30^\circ = \sin^2 36^\circ.</math>
			] used this proposition to compute some angles in ] in Book I, chapter 11 of '']''.
	then
	{|
	|&nbsp;&nbsp;&nbsp;||<math>\sin(x) = \frac{2t}{1 + t^2}</math>
	|&nbsp; and &nbsp;||<math>\cos(x) = \frac{1 - t^2}{1 + t^2}</math>
	|&nbsp; and &nbsp;||<math>e^{i x} = \frac{1 + i t}{1 - i t}.</math>
	|}
			== Composition of trigonometric functions ==
	where ''e<sup>''ix''</sup> is the same thing as cis(''x'').
			These identities involve a trigonometric function of a trigonometric function:<ref>], ], New York, 1972, formulae 9.1.42–9.1.45</ref>
			: <math>\cos(t \sin x) = J_0(t) + 2 \sum_{k=1}^\infty J_{2k}(t) \cos(2kx)</math>
	This substitution of ''t'' for tan(''x''/2), with the consequent replacement of sin(''x'') by 2''t''/(1 + ''t''²) and cos(''x'') by (1 &minus; ''t''²)/(1 + ''t''²) is useful in ] for converting rational functions in sin(''x'') and cos(''x'') to functions of ''t'' in order to find their antiderivatives. For more information see ].
			: <math>\sin(t \sin x) = 2 \sum_{k=0}^\infty J_{2k+1}(t) \sin\big((2k+1)x\big)</math>
			: <math>\cos(t \cos x) = J_0(t) + 2 \sum_{k=1}^\infty (-1)^kJ_{2k}(t) \cos(2kx)</math>
			: <math>\sin(t \cos x) = 2 \sum_{k=0}^\infty(-1)^k J_{2k+1}(t) \cos\big((2k+1)x\big)</math>
			where {{mvar|J<sub>i</sub>}} are ]s.
	==See also==
	*]
	*]
	*]
	*]
	*]
	*]
	*]
	*]
	*]
			== Further "conditional" identities for the case ''α'' + ''β'' + ''γ'' = 180° ==
	==References==
			A '''conditional trigonometric identity''' is a trigonometric identity that holds if specified conditions on the arguments to the trigonometric functions are satisfied.<ref>Er. K. C. Joshi, ''Krishna's IIT MATHEMATIKA''. Krishna Prakashan Media. Meerut, India. page 636.</ref> The following formulae apply to arbitrary plane triangles and follow from <math>\alpha + \beta + \gamma = 180^{\circ},</math> as long as the functions occurring in the formulae are well-defined (the latter applies only to the formulae in which tangents and cotangents occur).
	{{reflist}}
			<math display="block">\begin{align}
			\tan \alpha + \tan \beta + \tan \gamma &= \tan \alpha \tan \beta \tan \gamma \\
			1 &= \cot \beta \cot \gamma + \cot \gamma \cot \alpha + \cot \alpha \cot \beta \\
			\cot\left(\frac{\alpha}{2}\right) + \cot\left(\frac{\beta}{2}\right) + \cot\left(\frac{\gamma}{2}\right) &= \cot\left(\frac{\alpha}{2}\right) \cot \left(\frac{\beta}{2}\right) \cot\left(\frac{\gamma}{2}\right) \\
			1 &= \tan\left(\frac{\beta}{2}\right)\tan\left(\frac{\gamma}{2}\right) + \tan\left(\frac{\gamma}{2}\right)\tan\left(\frac{\alpha}{2}\right) + \tan\left(\frac{\alpha}{2}\right)\tan\left(\frac{\beta}{2}\right) \\
			\sin \alpha + \sin \beta + \sin \gamma &= 4\cos\left(\frac{\alpha}{2}\right)\cos\left(\frac{\beta}{2}\right)\cos\left(\frac{\gamma}{2}\right) \\
			-\sin \alpha + \sin \beta + \sin \gamma &= 4\cos\left(\frac{\alpha}{2}\right)\sin\left(\frac{\beta}{2}\right)\sin\left(\frac{\gamma}{2}\right) \\
			\cos \alpha + \cos \beta + \cos \gamma &= 4\sin\left(\frac{\alpha}{2}\right)\sin\left(\frac{\beta}{2}\right)\sin \left(\frac{\gamma}{2}\right) + 1 \\
			-\cos \alpha + \cos \beta + \cos \gamma &= 4\sin\left(\frac{\alpha}{2}\right)\cos\left(\frac{\beta}{2}\right)\cos \left(\frac{\gamma}{2}\right) - 1 \\
			\sin (2\alpha) + \sin (2\beta) + \sin (2\gamma) &= 4\sin \alpha \sin \beta \sin \gamma \\
			-\sin (2\alpha) + \sin (2\beta) + \sin (2\gamma) &= 4\sin \alpha \cos \beta \cos \gamma \\
			\cos (2\alpha) + \cos (2\beta) + \cos (2\gamma) &= -4\cos \alpha \cos \beta \cos \gamma - 1 \\
			-\cos (2\alpha) + \cos (2\beta) + \cos (2\gamma) &= -4\cos \alpha \sin \beta \sin \gamma + 1 \\
			\sin^2\alpha + \sin^2\beta + \sin^2\gamma &= 2 \cos \alpha \cos \beta \cos \gamma + 2 \\
			-\sin^2\alpha + \sin^2\beta + \sin^2\gamma &= 2 \cos \alpha \sin \beta \sin \gamma \\
			\cos^2\alpha + \cos^2\beta + \cos^2\gamma &= -2 \cos \alpha \cos \beta \cos \gamma + 1 \\
			-\cos^2\alpha + \cos^2\beta + \cos^2\gamma &= -2 \cos \alpha \sin \beta \sin \gamma + 1 \\
			\sin^2 (2\alpha) + \sin^2 (2\beta) + \sin^2 (2\gamma) &= -2\cos (2\alpha) \cos (2\beta) \cos (2\gamma)+2 \\
			\cos^2 (2\alpha) + \cos^2 (2\beta) + \cos^2 (2\gamma) &= 2\cos (2\alpha) \,\cos (2\beta) \,\cos (2\gamma) + 1 \\
			1 &= \sin^2 \left(\frac{\alpha}{2}\right) + \sin^2 \left(\frac{\beta}{2}\right) + \sin^2 \left(\frac{\gamma}{2}\right) + 2\sin \left(\frac{\alpha}{2}\right) \,\sin \left(\frac{\beta}{2}\right) \,\sin \left(\frac{\gamma}{2}\right)
			\end{align}</math>
			== Historical shorthands ==
	==External links==
			{{Main|Versine|Exsecant}}
			The ], ], ], and ] were used in navigation. For example, the ] was used to calculate the distance between two points on a sphere. They are rarely used today.
			==Miscellaneous==<!--This section will hopefully be sorted back into the article, If I can work out a place for the stuff to go-->
	]
	]
	]
			=== Dirichlet kernel ===
	]
			{{Main|Dirichlet kernel}}
	]
			The ''']''' {{math|''D<sub>n</sub>''(''x'')}} is the function occurring on both sides of the next identity:
	]
			<math display="block">1 + 2\cos x + 2\cos(2x) + 2\cos(3x) + \cdots + 2\cos(nx) = \frac{\sin\left(\left(n + \frac{1}{2}\right)x\right) }{\sin\left(\frac{1}{2}x\right)}.</math>
	]
	]
			The ] of any ] of period <math>2 \pi</math> with the Dirichlet kernel coincides with the function's <math>n</math>th-degree Fourier approximation. The same holds for any ] or ].
	]
	]
			=== Tangent half-angle substitution ===
	]
			{{Main|Tangent half-angle substitution}}
	]
	]
			If we set <math display="block">t = \tan\frac x 2,</math> then<ref>Abramowitz and Stegun, p.&nbsp;72, 4.3.23</ref>
	]
			<math display="block">\sin x = \frac{2t}{1 + t^2};\qquad \cos x = \frac{1 - t^2}{1 + t^2};\qquad e^{i x} = \frac{1 + i t}{1 - i t}; \qquad dx = \frac{2\,dt}{1+t^2}, </math>
	]
			where <math>e^{i x} = \cos x + i \sin x,</math> sometimes abbreviated to&nbsp;{{math|] ''x''}}.
	]
	]
			When this substitution of <math>t</math> for {{math|tan {{sfrac|''x''|2}}}} is used in ], it follows that <math>\sin x</math> is replaced by {{math|{{sfrac|2''t''|1 + ''t''<sup>2</sup>}}}}, <math>\cos x</math> is replaced by {{math|{{sfrac|1 − ''t''<sup>2</sup>|1 + ''t''<sup>2</sup>}}}} and the differential {{math|d''x''}} is replaced by {{math|{{sfrac|2 d''t''|1 + ''t''<sup>2</sup>}}}}. Thereby one converts rational functions of <math>\sin x</math> and <math>\cos x</math> to rational functions of <math>t</math> in order to find their ]s.
	]
			=== Viète's infinite product ===
			{{See also|Viète's formula|Sinc function}}
			<math display="block">\cos\frac{\theta}{2} \cdot \cos \frac{\theta}{4}
			\cdot \cos \frac{\theta}{8} \cdots = \prod_{n=1}^\infty \cos \frac{\theta}{2^n}
			= \frac{\sin \theta}{\theta} = \operatorname{sinc} \theta.</math>
			<!-- \operatorname{sinc} is intended to say "sinc", not "sin" and not "sine". --->
			== See also ==
			{{div col|colwidth=30em}}
			* ]
			* ]
			* ] (values of sine and cosine expressed in surds)
			* ]
			* ]
			* ]
			* Laws for solution of triangles:
			** ]
			*** ]
			** ]
			** ]
			** ]
			** ]
			* ]
			* ]
			* ]
			* ]
			* ]
			* ]
			* ]
			* ]
			* ]
			* ]
			* ] and ]
			{{div col end}}
			== References ==
			{{reflist|30em}}
			== Bibliography ==
			{{Refbegin}}
			* {{Cite book|editor1-last=Abramowitz|editor1-first=Milton|editor1-link=Milton Abramowitz|editor2-last=Stegun|editor2-first=Irene A.|editor2-link=Irene Stegun|title=Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables|publisher=]|location=New York|isbn=978-0-486-61272-0|year=1972|url=https://archive.org/details/handbookofmathe000abra }}
			* {{ citation|last1 = Nielsen|first1 = Kaj L.|title = Logarithmic and Trigonometric Tables to Five Places|edition = 2nd|location = New York|publisher = ]|year = 1966|lccn = 61-9103 }}
			* {{citation|editor-first=Samuel M.|editor-last=Selby|title=Standard Mathematical Tables|publisher=The Chemical Rubber Co.|year=1970|edition=18th}}
			{{Refend}}
			== External links ==
			* , and for the same angles and
			{{DEFAULTSORT:Trigonometric identities}}
			]
			]
			]

---

Latest revision as of 19:39, 24 December 2024

Trigonometry
Outline History Usage Functions (sin, cos, tan, inverse) Generalized trigonometry
Reference
Identities Exact constants Tables Unit circle
Laws and theorems
Sines Cosines Tangents Cotangents Pythagorean theorem
Calculus
Trigonometric substitution Integrals (inverse functions) Derivatives Trigonometric series
Mathematicians
Hipparchus Ptolemy Brahmagupta al-Hasib al-Battani Regiomontanus Viète de Moivre Euler Fourier
v t e

In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles. They are distinct from triangle identities, which are identities potentially involving angles but also involving side lengths or other lengths of a triangle.

These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the integration of non-trigonometric functions: a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity.

Pythagorean identities

Main article: Pythagorean trigonometric identity

The basic relationship between the sine and cosine is given by the Pythagorean identity:

$${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1,}$$

where ${\displaystyle \sin ^{2}\theta }$ means ${\displaystyle (\sin \theta )^{2}}$ and ${\displaystyle \cos ^{2}\theta }$ means ${\displaystyle (\cos \theta )^{2}.}$

This can be viewed as a version of the Pythagorean theorem, and follows from the equation ${\displaystyle x^{2}+y^{2}=1}$ for the unit circle. This equation can be solved for either the sine or the cosine:

$${\displaystyle {\begin{aligned}\sin \theta &=\pm {\sqrt {1-\cos ^{2}\theta }},\\\cos \theta &=\pm {\sqrt {1-\sin ^{2}\theta }}.\end{aligned}}}$$

where the sign depends on the quadrant of ${\displaystyle \theta .}$

Dividing this identity by ${\displaystyle \sin ^{2}\theta }$, ${\displaystyle \cos ^{2}\theta }$, or both yields the following identities: $${\displaystyle {\begin{aligned}&1+\cot ^{2}\theta =\csc ^{2}\theta \\&1+\tan ^{2}\theta =\sec ^{2}\theta \\&\sec ^{2}\theta +\csc ^{2}\theta =\sec ^{2}\theta \csc ^{2}\theta \end{aligned}}}$$

Using these identities, it is possible to express any trigonometric function in terms of any other (up to a plus or minus sign):

Each trigonometric function in terms of each of the other five.

in terms of	${\displaystyle \sin \theta }$	${\displaystyle \csc \theta }$	${\displaystyle \cos \theta }$	${\displaystyle \sec \theta }$	${\displaystyle \tan \theta }$	${\displaystyle \cot \theta }$
${\displaystyle \sin \theta =}$	${\displaystyle \sin \theta }$	${\displaystyle {\frac {1}{\csc \theta }}}$	${\displaystyle \pm {\sqrt {1-\cos ^{2}\theta }}}$	${\displaystyle \pm {\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}}$	${\displaystyle \pm {\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}}$	${\displaystyle \pm {\frac {1}{\sqrt {1+\cot ^{2}\theta }}}}$
${\displaystyle \csc \theta =}$	${\displaystyle {\frac {1}{\sin \theta }}}$	${\displaystyle \csc \theta }$	${\displaystyle \pm {\frac {1}{\sqrt {1-\cos ^{2}\theta }}}}$	${\displaystyle \pm {\frac {\sec \theta }{\sqrt {\sec ^{2}\theta -1}}}}$	${\displaystyle \pm {\frac {\sqrt {1+\tan ^{2}\theta }}{\tan \theta }}}$	${\displaystyle \pm {\sqrt {1+\cot ^{2}\theta }}}$
${\displaystyle \cos \theta =}$	${\displaystyle \pm {\sqrt {1-\sin ^{2}\theta }}}$	${\displaystyle \pm {\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}}$	${\displaystyle \cos \theta }$	${\displaystyle {\frac {1}{\sec \theta }}}$	${\displaystyle \pm {\frac {1}{\sqrt {1+\tan ^{2}\theta }}}}$	${\displaystyle \pm {\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}}$
${\displaystyle \sec \theta =}$	${\displaystyle \pm {\frac {1}{\sqrt {1-\sin ^{2}\theta }}}}$	${\displaystyle \pm {\frac {\csc \theta }{\sqrt {\csc ^{2}\theta -1}}}}$	${\displaystyle {\frac {1}{\cos \theta }}}$	${\displaystyle \sec \theta }$	${\displaystyle \pm {\sqrt {1+\tan ^{2}\theta }}}$	${\displaystyle \pm {\frac {\sqrt {1+\cot ^{2}\theta }}{\cot \theta }}}$
${\displaystyle \tan \theta =}$	${\displaystyle \pm {\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}}$	${\displaystyle \pm {\frac {1}{\sqrt {\csc ^{2}\theta -1}}}}$	${\displaystyle \pm {\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}}$	${\displaystyle \pm {\sqrt {\sec ^{2}\theta -1}}}$	${\displaystyle \tan \theta }$	${\displaystyle {\frac {1}{\cot \theta }}}$
${\displaystyle \cot \theta =}$	${\displaystyle \pm {\frac {\sqrt {1-\sin ^{2}\theta }}{\sin \theta }}}$	${\displaystyle \pm {\sqrt {\csc ^{2}\theta -1}}}$	${\displaystyle \pm {\frac {\cos \theta }{\sqrt {1-\cos ^{2}\theta }}}}$	${\displaystyle \pm {\frac {1}{\sqrt {\sec ^{2}\theta -1}}}}$	${\displaystyle {\frac {1}{\tan \theta }}}$	${\displaystyle \cot \theta }$

Reflections, shifts, and periodicity

By examining the unit circle, one can establish the following properties of the trigonometric functions.

Reflections

When the direction of a Euclidean vector is represented by an angle ${\displaystyle \theta ,}$ this is the angle determined by the free vector (starting at the origin) and the positive ${\displaystyle x}$-unit vector. The same concept may also be applied to lines in a Euclidean space, where the angle is that determined by a parallel to the given line through the origin and the positive ${\displaystyle x}$-axis. If a line (vector) with direction ${\displaystyle \theta }$ is reflected about a line with direction ${\displaystyle \alpha ,}$ then the direction angle ${\displaystyle \theta ^{\prime }}$ of this reflected line (vector) has the value $${\displaystyle \theta ^{\prime }=2\alpha -\theta .}$$

The values of the trigonometric functions of these angles ${\displaystyle \theta ,\;\theta ^{\prime }}$ for specific angles ${\displaystyle \alpha }$ satisfy simple identities: either they are equal, or have opposite signs, or employ the complementary trigonometric function. These are also known as reduction formulae.

${\displaystyle \theta }$ reflected in ${\displaystyle \alpha =0}$ odd/even identities	${\displaystyle \theta }$ reflected in ${\displaystyle \alpha ={\frac {\pi }{4}}}$	${\displaystyle \theta }$ reflected in ${\displaystyle \alpha ={\frac {\pi }{2}}}$	${\displaystyle \theta }$ reflected in ${\displaystyle \alpha ={\frac {3\pi }{4}}}$	${\displaystyle \theta }$ reflected in ${\displaystyle \alpha =\pi }$ compare to ${\displaystyle \alpha =0}$
${\displaystyle \sin(-\theta )=-\sin \theta }$	${\displaystyle \sin \left({\tfrac {\pi }{2}}-\theta \right)=\cos \theta }$	${\displaystyle \sin(\pi -\theta )=+\sin \theta }$	${\displaystyle \sin \left({\tfrac {3\pi }{2}}-\theta \right)=-\cos \theta }$	${\displaystyle \sin(2\pi -\theta )=-\sin(\theta )=\sin(-\theta )}$
${\displaystyle \cos(-\theta )=+\cos \theta }$	${\displaystyle \cos \left({\tfrac {\pi }{2}}-\theta \right)=\sin \theta }$	${\displaystyle \cos(\pi -\theta )=-\cos \theta }$	${\displaystyle \cos \left({\tfrac {3\pi }{2}}-\theta \right)=-\sin \theta }$	${\displaystyle \cos(2\pi -\theta )=+\cos(\theta )=\cos(-\theta )}$
${\displaystyle \tan(-\theta )=-\tan \theta }$	${\displaystyle \tan \left({\tfrac {\pi }{2}}-\theta \right)=\cot \theta }$	${\displaystyle \tan(\pi -\theta )=-\tan \theta }$	${\displaystyle \tan \left({\tfrac {3\pi }{2}}-\theta \right)=+\cot \theta }$	${\displaystyle \tan(2\pi -\theta )=-\tan(\theta )=\tan(-\theta )}$
${\displaystyle \csc(-\theta )=-\csc \theta }$	${\displaystyle \csc \left({\tfrac {\pi }{2}}-\theta \right)=\sec \theta }$	${\displaystyle \csc(\pi -\theta )=+\csc \theta }$	${\displaystyle \csc \left({\tfrac {3\pi }{2}}-\theta \right)=-\sec \theta }$	${\displaystyle \csc(2\pi -\theta )=-\csc(\theta )=\csc(-\theta )}$
${\displaystyle \sec(-\theta )=+\sec \theta }$	${\displaystyle \sec \left({\tfrac {\pi }{2}}-\theta \right)=\csc \theta }$	${\displaystyle \sec(\pi -\theta )=-\sec \theta }$	${\displaystyle \sec \left({\tfrac {3\pi }{2}}-\theta \right)=-\csc \theta }$	${\displaystyle \sec(2\pi -\theta )=+\sec(\theta )=\sec(-\theta )}$
${\displaystyle \cot(-\theta )=-\cot \theta }$	${\displaystyle \cot \left({\tfrac {\pi }{2}}-\theta \right)=\tan \theta }$	${\displaystyle \cot(\pi -\theta )=-\cot \theta }$	${\displaystyle \cot \left({\tfrac {3\pi }{2}}-\theta \right)=+\tan \theta }$	${\displaystyle \cot(2\pi -\theta )=-\cot(\theta )=\cot(-\theta )}$

Shifts and periodicity

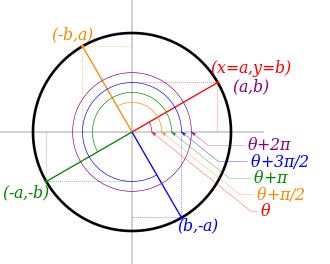
Shift by one quarter period	Shift by one half period	Shift by full periods	Period
${\displaystyle \sin(\theta \pm {\tfrac {\pi }{2}})=\pm \cos \theta }$	${\displaystyle \sin(\theta +\pi )=-\sin \theta }$	${\displaystyle \sin(\theta +k\cdot 2\pi )=+\sin \theta }$	${\displaystyle 2\pi }$
${\displaystyle \cos(\theta \pm {\tfrac {\pi }{2}})=\mp \sin \theta }$	${\displaystyle \cos(\theta +\pi )=-\cos \theta }$	${\displaystyle \cos(\theta +k\cdot 2\pi )=+\cos \theta }$	${\displaystyle 2\pi }$
${\displaystyle \csc(\theta \pm {\tfrac {\pi }{2}})=\pm \sec \theta }$	${\displaystyle \csc(\theta +\pi )=-\csc \theta }$	${\displaystyle \csc(\theta +k\cdot 2\pi )=+\csc \theta }$	${\displaystyle 2\pi }$
${\displaystyle \sec(\theta \pm {\tfrac {\pi }{2}})=\mp \csc \theta }$	${\displaystyle \sec(\theta +\pi )=-\sec \theta }$	${\displaystyle \sec(\theta +k\cdot 2\pi )=+\sec \theta }$	${\displaystyle 2\pi }$
${\displaystyle \tan(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\tan \theta \pm 1}{1\mp \tan \theta }}}$	${\displaystyle \tan(\theta +{\tfrac {\pi }{2}})=-\cot \theta }$	${\displaystyle \tan(\theta +k\cdot \pi )=+\tan \theta }$	${\displaystyle \pi }$
${\displaystyle \cot(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\cot \theta \mp 1}{1\pm \cot \theta }}}$	${\displaystyle \cot(\theta +{\tfrac {\pi }{2}})=-\tan \theta }$	${\displaystyle \cot(\theta +k\cdot \pi )=+\cot \theta }$	${\displaystyle \pi }$

Signs

The sign of trigonometric functions depends on quadrant of the angle. If ${\displaystyle {-\pi }<\theta \leq \pi }$ and sgn is the sign function,

$${\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta )=\operatorname {sgn}(\csc \theta )&={\begin{cases}+1&{\text{if}}\ \ 0<\theta <\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <0\\0&{\text{if}}\ \ \theta \in \{0,\pi \}\end{cases}}\\\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },{\tfrac {1}{2}}\pi {\bigr \}}\end{cases}}\\\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \theta )&={\begin{cases}+1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ 0<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <0\ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },0,{\tfrac {1}{2}}\pi ,\pi {\bigr \}}\end{cases}}\end{aligned}}}$$

The trigonometric functions are periodic with common period ${\displaystyle 2\pi ,}$ so for values of θ outside the interval ${\displaystyle ({-\pi },\pi ],}$ they take repeating values (see § Shifts and periodicity above).

Angle sum and difference identities

See also: Proofs of trigonometric identities § Angle sum identities, and Small-angle approximation § Angle sum and difference

These are also known as the angle addition and subtraction theorems (or formulae). $${\displaystyle {\begin{aligned}\sin(\alpha +\beta )&=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\\sin(\alpha -\beta )&=\sin \alpha \cos \beta -\cos \alpha \sin \beta \\\cos(\alpha +\beta )&=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\\cos(\alpha -\beta )&=\cos \alpha \cos \beta +\sin \alpha \sin \beta \end{aligned}}}$$

The angle difference identities for ${\displaystyle \sin(\alpha -\beta )}$ and ${\displaystyle \cos(\alpha -\beta )}$ can be derived from the angle sum versions by substituting ${\displaystyle -\beta }$ for ${\displaystyle \beta }$ and using the facts that ${\displaystyle \sin(-\beta )=-\sin(\beta )}$ and ${\displaystyle \cos(-\beta )=\cos(\beta )}$. They can also be derived by using a slightly modified version of the figure for the angle sum identities, both of which are shown here.

These identities are summarized in the first two rows of the following table, which also includes sum and difference identities for the other trigonometric functions.

Sine	${\displaystyle \sin(\alpha \pm \beta )}$			${\displaystyle =}$	${\displaystyle \sin \alpha \cos \beta \pm \cos \alpha \sin \beta }$
Cosine	${\displaystyle \cos(\alpha \pm \beta )}$			${\displaystyle =}$	${\displaystyle \cos \alpha \cos \beta \mp \sin \alpha \sin \beta }$
Tangent	${\displaystyle \tan(\alpha \pm \beta )}$			${\displaystyle =}$	${\displaystyle {\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}}$
Cosecant	${\displaystyle \csc(\alpha \pm \beta )}$			${\displaystyle =}$	${\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\sec \alpha \csc \beta \pm \csc \alpha \sec \beta }}}$
Secant	${\displaystyle \sec(\alpha \pm \beta )}$			${\displaystyle =}$	${\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\csc \alpha \csc \beta \mp \sec \alpha \sec \beta }}}$
Cotangent	${\displaystyle \cot(\alpha \pm \beta )}$			${\displaystyle =}$	${\displaystyle {\frac {\cot \alpha \cot \beta \mp 1}{\cot \beta \pm \cot \alpha }}}$
Arcsine	${\displaystyle \arcsin x\pm \arcsin y}$			${\displaystyle =}$	${\displaystyle \arcsin \left(x{\sqrt {1-y^{2}}}\pm y{\sqrt {1-x^{2}{\vphantom {y}}}}\right)}$
Arccosine	${\displaystyle \arccos x\pm \arccos y}$			${\displaystyle =}$	${\displaystyle \arccos \left(xy\mp {\sqrt {\left(1-x^{2}\right)\left(1-y^{2}\right)}}\right)}$
Arctangent	${\displaystyle \arctan x\pm \arctan y}$			${\displaystyle =}$	${\displaystyle \arctan \left({\frac {x\pm y}{1\mp xy}}\right)}$
Arccotangent	${\displaystyle \operatorname {arccot} x\pm \operatorname {arccot} y}$			${\displaystyle =}$	${\displaystyle \operatorname {arccot} \left({\frac {xy\mp 1}{y\pm x}}\right)}$

Sines and cosines of sums of infinitely many angles

When the series ${\textstyle \sum _{i=1}^{\infty }\theta _{i}}$ converges absolutely then

$${\displaystyle {\begin{aligned}{\sin }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggl )}&=\sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\!\!\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}\\{\cos }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggr )}&=\sum _{{\text{even}}\ k\geq 0}(-1)^{\frac {k}{2}}\,\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}.\end{aligned}}}$$

Because the series ${\textstyle \sum _{i=1}^{\infty }\theta _{i}}$ converges absolutely, it is necessarily the case that ${\textstyle \lim _{i\to \infty }\theta _{i}=0,}$ ${\textstyle \lim _{i\to \infty }\sin \theta _{i}=0,}$ and ${\textstyle \lim _{i\to \infty }\cos \theta _{i}=1.}$ In particular, in these two identities an asymmetry appears that is not seen in the case of sums of finitely many angles: in each product, there are only finitely many sine factors but there are cofinitely many cosine factors. Terms with infinitely many sine factors would necessarily be equal to zero.

When only finitely many of the angles ${\displaystyle \theta _{i}}$ are nonzero then only finitely many of the terms on the right side are nonzero because all but finitely many sine factors vanish. Furthermore, in each term all but finitely many of the cosine factors are unity.

Tangents and cotangents of sums

Let ${\displaystyle e_{k}}$ (for ${\displaystyle k=0,1,2,3,\ldots }$) be the kth-degree elementary symmetric polynomial in the variables $${\displaystyle x_{i}=\tan \theta _{i}}$$ for ${\displaystyle i=0,1,2,3,\ldots ,}$ that is,

$${\displaystyle {\begin{aligned}e_{0}&=1\\e_{1}&=\sum _{i}x_{i}&&=\sum _{i}\tan \theta _{i}\\e_{2}&=\sum _{i<j}x_{i}x_{j}&&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\\e_{3}&=\sum _{i<j<k}x_{i}x_{j}x_{k}&&=\sum _{i<j<k}\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&\ \ \vdots &&\ \ \vdots \end{aligned}}}$$

Then

$${\displaystyle {\begin{aligned}{\tan }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {{\sin }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}{{\cos }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}}\\&={\frac {\displaystyle \sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}{\displaystyle \sum _{{\text{even}}\ k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}}={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }}\\{\cot }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {e_{0}-e_{2}+e_{4}-\cdots }{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}$$

using the sine and cosine sum formulae above.

The number of terms on the right side depends on the number of terms on the left side.

For example: $${\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}={\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}$$

and so on. The case of only finitely many terms can be proved by mathematical induction. The case of infinitely many terms can be proved by using some elementary inequalities.

Secants and cosecants of sums

$${\displaystyle {\begin{aligned}{\sec }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{0}-e_{2}+e_{4}-\cdots }}\\{\csc }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}$$

where ${\displaystyle e_{k}}$ is the kth-degree elementary symmetric polynomial in the n variables ${\displaystyle x_{i}=\tan \theta _{i},}$ ${\displaystyle i=1,\ldots ,n,}$ and the number of terms in the denominator and the number of factors in the product in the numerator depend on the number of terms in the sum on the left. The case of only finitely many terms can be proved by mathematical induction on the number of such terms.

For example,

$${\displaystyle {\begin{aligned}\sec(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}\\\csc(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }}.\end{aligned}}}$$

Ptolemy's theorem

Main article: Ptolemy's theorem See also: History of trigonometry § Classical antiquity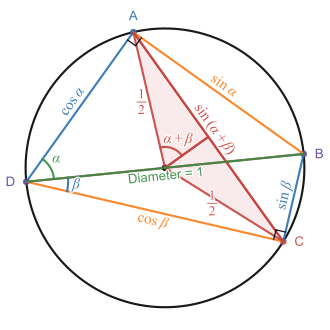

Ptolemy's theorem is important in the history of trigonometric identities, as it is how results equivalent to the sum and difference formulas for sine and cosine were first proved. It states that in a cyclic quadrilateral ${\displaystyle ABCD}$, as shown in the accompanying figure, the sum of the products of the lengths of opposite sides is equal to the product of the lengths of the diagonals. In the special cases of one of the diagonals or sides being a diameter of the circle, this theorem gives rise directly to the angle sum and difference trigonometric identities. The relationship follows most easily when the circle is constructed to have a diameter of length one, as shown here.

By Thales's theorem, ${\displaystyle \angle DAB}$ and ${\displaystyle \angle DCB}$ are both right angles. The right-angled triangles ${\displaystyle DAB}$ and ${\displaystyle DCB}$ both share the hypotenuse ${\displaystyle {\overline {BD}}}$ of length 1. Thus, the side ${\displaystyle {\overline {AB}}=\sin \alpha }$, ${\displaystyle {\overline {AD}}=\cos \alpha }$, ${\displaystyle {\overline {BC}}=\sin \beta }$ and ${\displaystyle {\overline {CD}}=\cos \beta }$.

By the inscribed angle theorem, the central angle subtended by the chord ${\displaystyle {\overline {AC}}}$ at the circle's center is twice the angle ${\displaystyle \angle ADC}$, i.e. ${\displaystyle 2(\alpha +\beta )}$. Therefore, the symmetrical pair of red triangles each has the angle ${\displaystyle \alpha +\beta }$ at the center. Each of these triangles has a hypotenuse of length ${\textstyle {\frac {1}{2}}}$, so the length of ${\displaystyle {\overline {AC}}}$ is ${\textstyle 2\times {\frac {1}{2}}\sin(\alpha +\beta )}$, i.e. simply ${\displaystyle \sin(\alpha +\beta )}$. The quadrilateral's other diagonal is the diameter of length 1, so the product of the diagonals' lengths is also ${\displaystyle \sin(\alpha +\beta )}$.

When these values are substituted into the statement of Ptolemy's theorem that ${\displaystyle |{\overline {AC}}|\cdot |{\overline {BD}}|=|{\overline {AB}}|\cdot |{\overline {CD}}|+|{\overline {AD}}|\cdot |{\overline {BC}}|}$, this yields the angle sum trigonometric identity for sine: ${\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta }$. The angle difference formula for ${\displaystyle \sin(\alpha -\beta )}$ can be similarly derived by letting the side ${\displaystyle {\overline {CD}}}$ serve as a diameter instead of ${\displaystyle {\overline {BD}}}$.

Multiple-angle and half-angle formulae

Tn is the nth Chebyshev polynomial	${\displaystyle \cos(n\theta )=T_{n}(\cos \theta )}$
de Moivre's formula, i is the imaginary unit	${\displaystyle \cos(n\theta )+i\sin(n\theta )=(\cos \theta +i\sin \theta )^{n}}$

Multiple-angle formulae

Double-angle formulae

Formulae for twice an angle.

• ${\displaystyle \sin(2\theta )=2\sin \theta \cos \theta =(\sin \theta +\cos \theta )^{2}-1={\frac {2\tan \theta }{1+\tan ^{2}\theta }}}$
• ${\displaystyle \cos(2\theta )=\cos ^{2}\theta -\sin ^{2}\theta =2\cos ^{2}\theta -1=1-2\sin ^{2}\theta ={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}}$
• ${\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}}$
• ${\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}={\frac {1-\tan ^{2}\theta }{2\tan \theta }}}$
• ${\displaystyle \sec(2\theta )={\frac {\sec ^{2}\theta }{2-\sec ^{2}\theta }}={\frac {1+\tan ^{2}\theta }{1-\tan ^{2}\theta }}}$
• ${\displaystyle \csc(2\theta )={\frac {\sec \theta \csc \theta }{2}}={\frac {1+\tan ^{2}\theta }{2\tan \theta }}}$

Triple-angle formulae

Formulae for triple angles.

• ${\displaystyle \sin(3\theta )=3\sin \theta -4\sin ^{3}\theta =4\sin \theta \sin \left({\frac {\pi }{3}}-\theta \right)\sin \left({\frac {\pi }{3}}+\theta \right)}$
• ${\displaystyle \cos(3\theta )=4\cos ^{3}\theta -3\cos \theta =4\cos \theta \cos \left({\frac {\pi }{3}}-\theta \right)\cos \left({\frac {\pi }{3}}+\theta \right)}$
• ${\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}=\tan \theta \tan \left({\frac {\pi }{3}}-\theta \right)\tan \left({\frac {\pi }{3}}+\theta \right)}$
• ${\displaystyle \cot(3\theta )={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}}$
• ${\displaystyle \sec(3\theta )={\frac {\sec ^{3}\theta }{4-3\sec ^{2}\theta }}}$
• ${\displaystyle \csc(3\theta )={\frac {\csc ^{3}\theta }{3\csc ^{2}\theta -4}}}$

Multiple-angle formulae

Formulae for multiple angles.

• ${\displaystyle {\begin{aligned}\sin(n\theta )&=\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sin \theta \sum _{i=0}^{(n+1)/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i+1}{i \choose j}\cos ^{n-2(i-j)-1}\theta \\{}&=\sin(\theta )\cdot \sum _{k=0}^{\left\lfloor {\frac {n-1}{2}}\right\rfloor }(-1)^{k}\cdot {(2\cdot \cos(\theta ))}^{n-2k-1}\cdot {n-k-1 \choose k}\\{}&=2^{(n-1)}\prod _{k=0}^{n-1}\sin(k\pi /n+\theta )\end{aligned}}}$
• ${\displaystyle {\begin{aligned}\cos(n\theta )&=\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sum _{i=0}^{n/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i}{i \choose j}\cos ^{n-2(i-j)}\theta \\{}&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }(-1)^{k}\cdot {(2\cdot \cos(\theta ))}^{n-2k}\cdot {n-k \choose k}\cdot {\frac {n}{2n-2k}}\end{aligned}}}$
• ${\displaystyle \cos((2n+1)\theta )=(-1)^{n}2^{2n}\prod _{k=0}^{2n}\cos(k\pi /(2n+1)-\theta )}$
• ${\displaystyle \cos(2n\theta )=(-1)^{n}2^{2n-1}\prod _{k=0}^{2n-1}\cos((1+2k)\pi /(4n)-\theta )}$
• ${\displaystyle \tan(n\theta )={\frac {\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\tan ^{k}\theta }{\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\tan ^{k}\theta }}}$

Chebyshev method

The Chebyshev method is a recursive algorithm for finding the nth multiple angle formula knowing the ${\displaystyle (n-1)}$th and ${\displaystyle (n-2)}$th values.

${\displaystyle \cos(nx)}$ can be computed from ${\displaystyle \cos((n-1)x)}$, ${\displaystyle \cos((n-2)x)}$, and ${\displaystyle \cos(x)}$ with

$${\displaystyle \cos(nx)=2\cos x\cos((n-1)x)-\cos((n-2)x).}$$

This can be proved by adding together the formulae

$${\displaystyle {\begin{aligned}\cos((n-1)x+x)&=\cos((n-1)x)\cos x-\sin((n-1)x)\sin x\\\cos((n-1)x-x)&=\cos((n-1)x)\cos x+\sin((n-1)x)\sin x\end{aligned}}}$$

It follows by induction that ${\displaystyle \cos(nx)}$ is a polynomial of ${\displaystyle \cos x,}$ the so-called Chebyshev polynomial of the first kind, see Chebyshev polynomials#Trigonometric definition.

Similarly, ${\displaystyle \sin(nx)}$ can be computed from ${\displaystyle \sin((n-1)x),}$ ${\displaystyle \sin((n-2)x),}$ and ${\displaystyle \cos x}$ with $${\displaystyle \sin(nx)=2\cos x\sin((n-1)x)-\sin((n-2)x)}$$ This can be proved by adding formulae for ${\displaystyle \sin((n-1)x+x)}$ and ${\displaystyle \sin((n-1)x-x).}$

Serving a purpose similar to that of the Chebyshev method, for the tangent we can write:

$${\displaystyle \tan(nx)={\frac {\tan((n-1)x)+\tan x}{1-\tan((n-1)x)\tan x}}\,.}$$

Half-angle formulae

$${\displaystyle {\begin{aligned}\sin {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\\cos {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\\tan {\frac {\theta }{2}}&={\frac {1-\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1+\cos \theta }}=\csc \theta -\cot \theta ={\frac {\tan \theta }{1+\sec {\theta }}}\\&=\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {-1+\operatorname {sgn}(\cos \theta ){\sqrt {1+\tan ^{2}\theta }}}{\tan \theta }}\\\cot {\frac {\theta }{2}}&={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta =\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\\sec {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1+\cos \theta }}}\\\csc {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1-\cos \theta }}}\\\end{aligned}}}$$

Also $${\displaystyle {\begin{aligned}\tan {\frac {\eta \pm \theta }{2}}&={\frac {\sin \eta \pm \sin \theta }{\cos \eta +\cos \theta }}\\\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\end{aligned}}}$$

Table

See also: Tangent half-angle formula

These can be shown by using either the sum and difference identities or the multiple-angle formulae.

	Sine	Cosine	Tangent	Cotangent
Double-angle formula	${\displaystyle {\begin{aligned}\sin(2\theta )&=2\sin \theta \cos \theta \ \\&={\frac {2\tan \theta }{1+\tan ^{2}\theta }}\end{aligned}}}$	${\displaystyle {\begin{aligned}\cos(2\theta )&=\cos ^{2}\theta -\sin ^{2}\theta \\&=2\cos ^{2}\theta -1\\&=1-2\sin ^{2}\theta \\&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}}}$	${\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}}$	${\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}}$
Triple-angle formula	${\displaystyle {\begin{aligned}\sin(3\theta )&=-\sin ^{3}\theta +3\cos ^{2}\theta \sin \theta \\&=-4\sin ^{3}\theta +3\sin \theta \end{aligned}}}$	${\displaystyle {\begin{aligned}\cos(3\theta )&=\cos ^{3}\theta -3\sin ^{2}\theta \cos \theta \\&=4\cos ^{3}\theta -3\cos \theta \end{aligned}}}$	${\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}}$	${\displaystyle \cot(3\theta )={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}}$
Half-angle formula	${\displaystyle {\begin{aligned}&\sin {\frac {\theta }{2}}=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\\\&\left({\text{or }}\sin ^{2}{\frac {\theta }{2}}={\frac {1-\cos \theta }{2}}\right)\end{aligned}}}$	${\displaystyle {\begin{aligned}&\cos {\frac {\theta }{2}}=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\\\&\left({\text{or }}\cos ^{2}{\frac {\theta }{2}}={\frac {1+\cos \theta }{2}}\right)\end{aligned}}}$	${\displaystyle {\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}\\&={\frac {\sin \theta }{1+\cos \theta }}\\&={\frac {1-\cos \theta }{\sin \theta }}\\\tan {\frac {\eta +\theta }{2}}&={\frac {\sin \eta +\sin \theta }{\cos \eta +\cos \theta }}\\\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\\\tan {\frac {\theta }{2}}&={\frac {\tan \theta }{1+{\sqrt {1+\tan ^{2}\theta }}}}\\&{\text{for }}\theta \in \left(-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right)\end{aligned}}}$	${\displaystyle {\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\&={\frac {\sin \theta }{1-\cos \theta }}\\&={\frac {1+\cos \theta }{\sin \theta }}\end{aligned}}}$

The fact that the triple-angle formula for sine and cosine only involves powers of a single function allows one to relate the geometric problem of a compass and straightedge construction of angle trisection to the algebraic problem of solving a cubic equation, which allows one to prove that trisection is in general impossible using the given tools.

A formula for computing the trigonometric identities for the one-third angle exists, but it requires finding the zeroes of the cubic equation 4x − 3x + d = 0, where ${\displaystyle x}$ is the value of the cosine function at the one-third angle and d is the known value of the cosine function at the full angle. However, the discriminant of this equation is positive, so this equation has three real roots (of which only one is the solution for the cosine of the one-third angle). None of these solutions are reducible to a real algebraic expression, as they use intermediate complex numbers under the cube roots.

Power-reduction formulae

Obtained by solving the second and third versions of the cosine double-angle formula.

Sine	Cosine	Other
${\displaystyle \sin ^{2}\theta ={\frac {1-\cos(2\theta )}{2}}}$	${\displaystyle \cos ^{2}\theta ={\frac {1+\cos(2\theta )}{2}}}$	${\displaystyle \sin ^{2}\theta \cos ^{2}\theta ={\frac {1-\cos(4\theta )}{8}}}$
${\displaystyle \sin ^{3}\theta ={\frac {3\sin \theta -\sin(3\theta )}{4}}}$	${\displaystyle \cos ^{3}\theta ={\frac {3\cos \theta +\cos(3\theta )}{4}}}$	${\displaystyle \sin ^{3}\theta \cos ^{3}\theta ={\frac {3\sin(2\theta )-\sin(6\theta )}{32}}}$
${\displaystyle \sin ^{4}\theta ={\frac {3-4\cos(2\theta )+\cos(4\theta )}{8}}}$	${\displaystyle \cos ^{4}\theta ={\frac {3+4\cos(2\theta )+\cos(4\theta )}{8}}}$	${\displaystyle \sin ^{4}\theta \cos ^{4}\theta ={\frac {3-4\cos(4\theta )+\cos(8\theta )}{128}}}$
${\displaystyle \sin ^{5}\theta ={\frac {10\sin \theta -5\sin(3\theta )+\sin(5\theta )}{16}}}$	${\displaystyle \cos ^{5}\theta ={\frac {10\cos \theta +5\cos(3\theta )+\cos(5\theta )}{16}}}$	${\displaystyle \sin ^{5}\theta \cos ^{5}\theta ={\frac {10\sin(2\theta )-5\sin(6\theta )+\sin(10\theta )}{512}}}$

In general terms of powers of ${\displaystyle \sin \theta }$ or ${\displaystyle \cos \theta }$ the following is true, and can be deduced using De Moivre's formula, Euler's formula and the binomial theorem.

if n is ...	${\displaystyle \cos ^{n}\theta }$	${\displaystyle \sin ^{n}\theta }$
n is odd	${\displaystyle \cos ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}}$	${\displaystyle \sin ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}(-1)^{\left({\frac {n-1}{2}}-k\right)}{\binom {n}{k}}\sin {{\big (}(n-2k)\theta {\big )}}}$
n is even	${\displaystyle \cos ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}}$	${\displaystyle \sin ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}(-1)^{\left({\frac {n}{2}}-k\right)}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}}$

Product-to-sum and sum-to-product identities

The product-to-sum identities or prosthaphaeresis formulae can be proven by expanding their right-hand sides using the angle addition theorems. Historically, the first four of these were known as Werner's formulas, after Johannes Werner who used them for astronomical calculations. See amplitude modulation for an application of the product-to-sum formulae, and beat (acoustics) and phase detector for applications of the sum-to-product formulae.

Product-to-sum identities

• ${\displaystyle {\begin{aligned}\cos \theta \,\cos \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\cos(\theta -\varphi )+\cos(\theta +\varphi ){\bigr )}\\\sin \theta \,\sin \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\cos(\theta -\varphi )-\cos(\theta +\varphi ){\bigr )}\\\sin \theta \,\cos \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\sin(\theta +\varphi )+\sin(\theta -\varphi ){\bigr )}\\\cos \theta \,\sin \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\sin(\theta +\varphi )-\sin(\theta -\varphi ){\bigr )}\end{aligned}}}$
• ${\displaystyle \tan \theta \,\tan \varphi ={\frac {\cos(\theta -\varphi )-\cos(\theta +\varphi )}{\cos(\theta -\varphi )+\cos(\theta +\varphi )}}}$
• ${\displaystyle \tan \theta \,\cot \varphi ={\frac {\sin(\theta +\varphi )+\sin(\theta -\varphi )}{\sin(\theta +\varphi )-\sin(\theta -\varphi )}}}$
• ${\displaystyle {\begin{aligned}\prod _{k=1}^{n}\cos \theta _{k}&={\frac {1}{2^{n}}}\sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\\&{\text{where }}e=(e_{1},\ldots ,e_{n})\in S=\{1,-1\}^{n}\end{aligned}}}$
• ${\displaystyle \prod _{k=1}^{n}\sin \theta _{k}={\frac {(-1)^{\left\lfloor {\frac {n}{2}}\right\rfloor }}{2^{n}}}{\begin{cases}\displaystyle \sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\prod _{j=1}^{n}e_{j}\;{\text{if}}\;n\;{\text{is even}},\\\displaystyle \sum _{e\in S}\sin(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\prod _{j=1}^{n}e_{j}\;{\text{if}}\;n\;{\text{is odd}}\end{cases}}}$

Sum-to-product identities

The sum-to-product identities are as follows:

• ${\displaystyle \sin \theta \pm \sin \varphi =2\sin \left({\frac {\theta \pm \varphi }{2}}\right)\cos \left({\frac {\theta \mp \varphi }{2}}\right)}$
• ${\displaystyle \cos \theta +\cos \varphi =2\cos \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)}$
• ${\displaystyle \cos \theta -\cos \varphi =-2\sin \left({\frac {\theta +\varphi }{2}}\right)\sin \left({\frac {\theta -\varphi }{2}}\right)}$
• ${\displaystyle \tan \theta \pm \tan \varphi ={\frac {\sin(\theta \pm \varphi )}{\cos \theta \,\cos \varphi }}}$

Hermite's cotangent identity

Main article: Hermite's cotangent identity

Charles Hermite demonstrated the following identity. Suppose ${\displaystyle a_{1},\ldots ,a_{n}}$ are complex numbers, no two of which differ by an integer multiple of π. Let

$${\displaystyle A_{n,k}=\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq k\end{smallmatrix}}\cot(a_{k}-a_{j})}$$

(in particular, ${\displaystyle A_{1,1},}$ being an empty product, is 1). Then

$${\displaystyle \cot(z-a_{1})\cdots \cot(z-a_{n})=\cos {\frac {n\pi }{2}}+\sum _{k=1}^{n}A_{n,k}\cot(z-a_{k}).}$$

The simplest non-trivial example is the case n = 2:

$${\displaystyle \cot(z-a_{1})\cot(z-a_{2})=-1+\cot(a_{1}-a_{2})\cot(z-a_{1})+\cot(a_{2}-a_{1})\cot(z-a_{2}).}$$

Finite products of trigonometric functions

For coprime integers n, m

$${\displaystyle \prod _{k=1}^{n}\left(2a+2\cos \left({\frac {2\pi km}{n}}+x\right)\right)=2\left(T_{n}(a)+{(-1)}^{n+m}\cos(nx)\right)}$$

where T_n is the Chebyshev polynomial.

The following relationship holds for the sine function

$${\displaystyle \prod _{k=1}^{n-1}\sin \left({\frac {k\pi }{n}}\right)={\frac {n}{2^{n-1}}}.}$$

More generally for an integer n > 0

$${\displaystyle \sin(nx)=2^{n-1}\prod _{k=0}^{n-1}\sin \left({\frac {k}{n}}\pi +x\right)=2^{n-1}\prod _{k=1}^{n}\sin \left({\frac {k}{n}}\pi -x\right).}$$

or written in terms of the chord function ${\textstyle \operatorname {crd} x\equiv 2\sin {\tfrac {1}{2}}x}$,

$${\displaystyle \operatorname {crd} (nx)=\prod _{k=1}^{n}\operatorname {crd} \left({\frac {k}{n}}2\pi -x\right).}$$

This comes from the factorization of the polynomial ${\textstyle z^{n}-1}$ into linear factors (cf. root of unity): For any complex z and an integer n > 0,

$${\displaystyle z^{n}-1=\prod _{k=1}^{n}\left(z-\exp {\Bigl (}{\frac {k}{n}}2\pi i{\Bigr )}\right).}$$

Linear combinations

For some purposes it is important to know that any linear combination of sine waves of the same period or frequency but different phase shifts is also a sine wave with the same period or frequency, but a different phase shift. This is useful in sinusoid data fitting, because the measured or observed data are linearly related to the a and b unknowns of the in-phase and quadrature components basis below, resulting in a simpler Jacobian, compared to that of ${\displaystyle c}$ and ${\displaystyle \varphi }$.

Sine and cosine

The linear combination, or harmonic addition, of sine and cosine waves is equivalent to a single sine wave with a phase shift and scaled amplitude,

$${\displaystyle a\cos x+b\sin x=c\cos(x+\varphi )}$$

where ${\displaystyle c}$ and ${\displaystyle \varphi }$ are defined as so:

$${\displaystyle {\begin{aligned}c&=\operatorname {sgn}(a){\sqrt {a^{2}+b^{2}}},\\\varphi &={\arctan }{\bigl (}{-b/a}{\bigr )},\end{aligned}}}$$

given that ${\displaystyle a\neq 0.}$

Arbitrary phase shift

More generally, for arbitrary phase shifts, we have

$${\displaystyle a\sin(x+\theta _{a})+b\sin(x+\theta _{b})=c\sin(x+\varphi )}$$

where ${\displaystyle c}$ and ${\displaystyle \varphi }$ satisfy:

$${\displaystyle {\begin{aligned}c^{2}&=a^{2}+b^{2}+2ab\cos \left(\theta _{a}-\theta _{b}\right),\\\tan \varphi &={\frac {a\sin \theta _{a}+b\sin \theta _{b}}{a\cos \theta _{a}+b\cos \theta _{b}}}.\end{aligned}}}$$

More than two sinusoids

See also: Phasor addition

The general case reads

$${\displaystyle \sum _{i}a_{i}\sin(x+\theta _{i})=a\sin(x+\theta ),}$$ where $${\displaystyle a^{2}=\sum _{i,j}a_{i}a_{j}\cos(\theta _{i}-\theta _{j})}$$ and $${\displaystyle \tan \theta ={\frac {\sum _{i}a_{i}\sin \theta _{i}}{\sum _{i}a_{i}\cos \theta _{i}}}.}$$

Lagrange's trigonometric identities

These identities, named after Joseph Louis Lagrange, are: $${\displaystyle {\begin{aligned}\sum _{k=0}^{n}\sin k\theta &={\frac {\cos {\tfrac {1}{2}}\theta -\cos \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\\\sum _{k=0}^{n}\cos k\theta &={\frac {\sin {\tfrac {1}{2}}\theta +\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\end{aligned}}}$$ for ${\displaystyle \theta \not \equiv 0{\pmod {2\pi }}.}$

A related function is the Dirichlet kernel:

$${\displaystyle D_{n}(\theta )=1+2\sum _{k=1}^{n}\cos k\theta ={\frac {\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{\sin {\tfrac {1}{2}}\theta }}.}$$

A similar identity is

$${\displaystyle \sum _{k=1}^{n}\cos(2k-1)\alpha ={\frac {\sin(2n\alpha )}{2\sin \alpha }}.}$$

The proof is the following. By using the angle sum and difference identities, $${\displaystyle \sin(A+B)-\sin(A-B)=2\cos A\sin B.}$$ Then let's examine the following formula,

$${\displaystyle 2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha =2\sin \alpha \cos \alpha +2\sin \alpha \cos 3\alpha +2\sin \alpha \cos 5\alpha +\ldots +2\sin \alpha \cos(2n-1)\alpha }$$ and this formula can be written by using the above identity,

$${\displaystyle {\begin{aligned}&2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha \\&\quad =\sum _{k=1}^{n}(\sin(2k\alpha )-\sin(2(k-1)\alpha ))\\&\quad =(\sin 2\alpha -\sin 0)+(\sin 4\alpha -\sin 2\alpha )+(\sin 6\alpha -\sin 4\alpha )+\ldots +(\sin(2n\alpha )-\sin(2(n-1)\alpha ))\\&\quad =\sin(2n\alpha ).\end{aligned}}}$$

So, dividing this formula with ${\displaystyle 2\sin \alpha }$ completes the proof.

Certain linear fractional transformations

If ${\displaystyle f(x)}$ is given by the linear fractional transformation $${\displaystyle f(x)={\frac {(\cos \alpha )x-\sin \alpha }{(\sin \alpha )x+\cos \alpha }},}$$ and similarly $${\displaystyle g(x)={\frac {(\cos \beta )x-\sin \beta }{(\sin \beta )x+\cos \beta }},}$$ then $${\displaystyle f{\big (}g(x){\big )}=g{\big (}f(x){\big )}={\frac {{\big (}\cos(\alpha +\beta ){\big )}x-\sin(\alpha +\beta )}{{\big (}\sin(\alpha +\beta ){\big )}x+\cos(\alpha +\beta )}}.}$$

More tersely stated, if for all ${\displaystyle \alpha }$ we let ${\displaystyle f_{\alpha }}$ be what we called ${\displaystyle f}$ above, then $${\displaystyle f_{\alpha }\circ f_{\beta }=f_{\alpha +\beta }.}$$

If ${\displaystyle x}$ is the slope of a line, then ${\displaystyle f(x)}$ is the slope of its rotation through an angle of ${\displaystyle -\alpha .}$

Relation to the complex exponential function

Main article: Euler's formula

Euler's formula states that, for any real number x: $${\displaystyle e^{ix}=\cos x+i\sin x,}$$ where i is the imaginary unit. Substituting −x for x gives us: $${\displaystyle e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x.}$$

These two equations can be used to solve for cosine and sine in terms of the exponential function. Specifically, $${\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}}$$ $${\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}}$$

These formulae are useful for proving many other trigonometric identities. For example, that e = e e means that

cos(θ + φ) + i sin(θ + φ) = (cos θ + i sin θ) (cos φ + i sin φ) = (cos θ cos φ − sin θ sin φ) + i (cos θ sin φ + sin θ cos φ).

That the real part of the left hand side equals the real part of the right hand side is an angle addition formula for cosine. The equality of the imaginary parts gives an angle addition formula for sine.

The following table expresses the trigonometric functions and their inverses in terms of the exponential function and the complex logarithm.

Function	Inverse function
${\displaystyle \sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}}$	${\displaystyle \arcsin x=-i\,\ln \left(ix+{\sqrt {1-x^{2}}}\right)}$
${\displaystyle \cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}}$	${\displaystyle \arccos x=-i\ln \left(x+{\sqrt {x^{2}-1}}\right)}$
${\displaystyle \tan \theta =-i\,{\frac {e^{i\theta }-e^{-i\theta }}{e^{i\theta }+e^{-i\theta }}}}$	${\displaystyle \arctan x={\frac {i}{2}}\ln \left({\frac {i+x}{i-x}}\right)}$
${\displaystyle \csc \theta ={\frac {2i}{e^{i\theta }-e^{-i\theta }}}}$	${\displaystyle \operatorname {arccsc} x=-i\,\ln \left({\frac {i}{x}}+{\sqrt {1-{\frac {1}{x^{2}}}}}\right)}$
${\displaystyle \sec \theta ={\frac {2}{e^{i\theta }+e^{-i\theta }}}}$	${\displaystyle \operatorname {arcsec} x=-i\,\ln \left({\frac {1}{x}}+i{\sqrt {1-{\frac {1}{x^{2}}}}}\right)}$
${\displaystyle \cot \theta =i\,{\frac {e^{i\theta }+e^{-i\theta }}{e^{i\theta }-e^{-i\theta }}}}$	${\displaystyle \operatorname {arccot} x={\frac {i}{2}}\ln \left({\frac {x-i}{x+i}}\right)}$
${\displaystyle \operatorname {cis} \theta =e^{i\theta }}$	${\displaystyle \operatorname {arccis} x=-i\ln x}$

Relation to complex hyperbolic functions

Trigonometric functions may be deduced from hyperbolic functions with complex arguments. The formulae for the relations are shown below.$${\displaystyle {\begin{aligned}\sin x&=-i\sinh(ix)\\\cos x&=\cosh(ix)\\\tan x&=-i\tanh(ix)\\\cot x&=i\coth(ix)\\\sec x&=\operatorname {sech} (ix)\\\csc x&=i\operatorname {csch} (ix)\\\end{aligned}}}$$

Series expansion

When using a power series expansion to define trigonometric functions, the following identities are obtained:

$${\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},}$$$${\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.}$$

Infinite product formulae

For applications to special functions, the following infinite product formulae for trigonometric functions are useful:

$${\displaystyle {\begin{aligned}\sin x&=x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cos x&=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right),\\\sinh x&=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cosh x&=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right).\end{aligned}}}$$

Inverse trigonometric functions

Main article: Inverse trigonometric functions

The following identities give the result of composing a trigonometric function with an inverse trigonometric function.

$${\displaystyle {\begin{aligned}\sin(\arcsin x)&=x&\cos(\arcsin x)&={\sqrt {1-x^{2}}}&\tan(\arcsin x)&={\frac {x}{\sqrt {1-x^{2}}}}\\\sin(\arccos x)&={\sqrt {1-x^{2}}}&\cos(\arccos x)&=x&\tan(\arccos x)&={\frac {\sqrt {1-x^{2}}}{x}}\\\sin(\arctan x)&={\frac {x}{\sqrt {1+x^{2}}}}&\cos(\arctan x)&={\frac {1}{\sqrt {1+x^{2}}}}&\tan(\arctan x)&=x\\\sin(\operatorname {arccsc} x)&={\frac {1}{x}}&\cos(\operatorname {arccsc} x)&={\frac {\sqrt {x^{2}-1}}{x}}&\tan(\operatorname {arccsc} x)&={\frac {1}{\sqrt {x^{2}-1}}}\\\sin(\operatorname {arcsec} x)&={\frac {\sqrt {x^{2}-1}}{x}}&\cos(\operatorname {arcsec} x)&={\frac {1}{x}}&\tan(\operatorname {arcsec} x)&={\sqrt {x^{2}-1}}\\\sin(\operatorname {arccot} x)&={\frac {1}{\sqrt {1+x^{2}}}}&\cos(\operatorname {arccot} x)&={\frac {x}{\sqrt {1+x^{2}}}}&\tan(\operatorname {arccot} x)&={\frac {1}{x}}\\\end{aligned}}}$$

Taking the multiplicative inverse of both sides of the each equation above results in the equations for ${\displaystyle \csc ={\frac {1}{\sin }},\;\sec ={\frac {1}{\cos }},{\text{ and }}\cot ={\frac {1}{\tan }}.}$ The right hand side of the formula above will always be flipped. For example, the equation for ${\displaystyle \cot(\arcsin x)}$ is: $${\displaystyle \cot(\arcsin x)={\frac {1}{\tan(\arcsin x)}}={\frac {1}{\frac {x}{\sqrt {1-x^{2}}}}}={\frac {\sqrt {1-x^{2}}}{x}}}$$ while the equations for ${\displaystyle \csc(\arccos x)}$ and ${\displaystyle \sec(\arccos x)}$ are: $${\displaystyle \csc(\arccos x)={\frac {1}{\sin(\arccos x)}}={\frac {1}{\sqrt {1-x^{2}}}}\qquad {\text{ and }}\quad \sec(\arccos x)={\frac {1}{\cos(\arccos x)}}={\frac {1}{x}}.}$$

The following identities are implied by the reflection identities. They hold whenever ${\displaystyle x,r,s,-x,-r,{\text{ and }}-s}$ are in the domains of the relevant functions. $${\displaystyle {\begin{alignedat}{9}{\frac {\pi }{2}}~&=~\arcsin(x)&&+\arccos(x)~&&=~\arctan(r)&&+\operatorname {arccot}(r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arccsc}(s)\\\pi ~&=~\arccos(x)&&+\arccos(-x)~&&=~\operatorname {arccot}(r)&&+\operatorname {arccot}(-r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arcsec}(-s)\\0~&=~\arcsin(x)&&+\arcsin(-x)~&&=~\arctan(r)&&+\arctan(-r)~&&=~\operatorname {arccsc}(s)&&+\operatorname {arccsc}(-s)\\\end{alignedat}}}$$

Also, $${\displaystyle {\begin{aligned}\arctan x+\arctan {\dfrac {1}{x}}&={\begin{cases}{\frac {\pi }{2}},&{\text{if }}x>0\\-{\frac {\pi }{2}},&{\text{if }}x<0\end{cases}}\\\operatorname {arccot} x+\operatorname {arccot} {\dfrac {1}{x}}&={\begin{cases}{\frac {\pi }{2}},&{\text{if }}x>0\\{\frac {3\pi }{2}},&{\text{if }}x<0\end{cases}}\\\end{aligned}}}$$ $${\displaystyle \arccos {\frac {1}{x}}=\operatorname {arcsec} x\qquad {\text{ and }}\qquad \operatorname {arcsec} {\frac {1}{x}}=\arccos x}$$ $${\displaystyle \arcsin {\frac {1}{x}}=\operatorname {arccsc} x\qquad {\text{ and }}\qquad \operatorname {arccsc} {\frac {1}{x}}=\arcsin x}$$

The arctangent function can be expanded as a series: $${\displaystyle \arctan(nx)=\sum _{m=1}^{n}\arctan {\frac {x}{1+(m-1)mx^{2}}}}$$

Identities without variables

In terms of the arctangent function we have $${\displaystyle \arctan {\frac {1}{2}}=\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}.}$$

The curious identity known as Morrie's law, $${\displaystyle \cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\frac {1}{8}},}$$

is a special case of an identity that contains one variable: $${\displaystyle \prod _{j=0}^{k-1}\cos \left(2^{j}x\right)={\frac {\sin \left(2^{k}x\right)}{2^{k}\sin x}}.}$$

Similarly, $${\displaystyle \sin 20^{\circ }\cdot \sin 40^{\circ }\cdot \sin 80^{\circ }={\frac {\sqrt {3}}{8}}}$$ is a special case of an identity with ${\displaystyle x=20^{\circ }}$: $${\displaystyle \sin x\cdot \sin \left(60^{\circ }-x\right)\cdot \sin \left(60^{\circ }+x\right)={\frac {\sin 3x}{4}}.}$$

For the case ${\displaystyle x=15^{\circ }}$, $${\displaystyle {\begin{aligned}\sin 15^{\circ }\cdot \sin 45^{\circ }\cdot \sin 75^{\circ }&={\frac {\sqrt {2}}{8}},\\\sin 15^{\circ }\cdot \sin 75^{\circ }&={\frac {1}{4}}.\end{aligned}}}$$

For the case ${\displaystyle x=10^{\circ }}$, $${\displaystyle \sin 10^{\circ }\cdot \sin 50^{\circ }\cdot \sin 70^{\circ }={\frac {1}{8}}.}$$

The same cosine identity is $${\displaystyle \cos x\cdot \cos \left(60^{\circ }-x\right)\cdot \cos \left(60^{\circ }+x\right)={\frac {\cos 3x}{4}}.}$$

Similarly, $${\displaystyle {\begin{aligned}\cos 10^{\circ }\cdot \cos 50^{\circ }\cdot \cos 70^{\circ }&={\frac {\sqrt {3}}{8}},\\\cos 15^{\circ }\cdot \cos 45^{\circ }\cdot \cos 75^{\circ }&={\frac {\sqrt {2}}{8}},\\\cos 15^{\circ }\cdot \cos 75^{\circ }&={\frac {1}{4}}.\end{aligned}}}$$

Similarly, $${\displaystyle {\begin{aligned}\tan 50^{\circ }\cdot \tan 60^{\circ }\cdot \tan 70^{\circ }&=\tan 80^{\circ },\\\tan 40^{\circ }\cdot \tan 30^{\circ }\cdot \tan 20^{\circ }&=\tan 10^{\circ }.\end{aligned}}}$$

The following is perhaps not as readily generalized to an identity containing variables (but see explanation below): $${\displaystyle \cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }={\frac {1}{2}}.}$$

Degree measure ceases to be more felicitous than radian measure when we consider this identity with 21 in the denominators: $${\displaystyle \cos {\frac {2\pi }{21}}+\cos \left(2\cdot {\frac {2\pi }{21}}\right)+\cos \left(4\cdot {\frac {2\pi }{21}}\right)+\cos \left(5\cdot {\frac {2\pi }{21}}\right)+\cos \left(8\cdot {\frac {2\pi }{21}}\right)+\cos \left(10\cdot {\frac {2\pi }{21}}\right)={\frac {1}{2}}.}$$

The factors 1, 2, 4, 5, 8, 10 may start to make the pattern clear: they are those integers less than ⁠21/2⁠ that are relatively prime to (or have no prime factors in common with) 21. The last several examples are corollaries of a basic fact about the irreducible cyclotomic polynomials: the cosines are the real parts of the zeroes of those polynomials; the sum of the zeroes is the Möbius function evaluated at (in the very last case above) 21; only half of the zeroes are present above. The two identities preceding this last one arise in the same fashion with 21 replaced by 10 and 15, respectively.

Other cosine identities include: $${\displaystyle {\begin{aligned}2\cos {\frac {\pi }{3}}&=1,\\2\cos {\frac {\pi }{5}}\times 2\cos {\frac {2\pi }{5}}&=1,\\2\cos {\frac {\pi }{7}}\times 2\cos {\frac {2\pi }{7}}\times 2\cos {\frac {3\pi }{7}}&=1,\end{aligned}}}$$ and so forth for all odd numbers, and hence $${\displaystyle \cos {\frac {\pi }{3}}+\cos {\frac {\pi }{5}}\times \cos {\frac {2\pi }{5}}+\cos {\frac {\pi }{7}}\times \cos {\frac {2\pi }{7}}\times \cos {\frac {3\pi }{7}}+\dots =1.}$$

Many of those curious identities stem from more general facts like the following: $${\displaystyle \prod _{k=1}^{n-1}\sin {\frac {k\pi }{n}}={\frac {n}{2^{n-1}}}}$$ and $${\displaystyle \prod _{k=1}^{n-1}\cos {\frac {k\pi }{n}}={\frac {\sin {\frac {\pi n}{2}}}{2^{n-1}}}.}$$

Combining these gives us $${\displaystyle \prod _{k=1}^{n-1}\tan {\frac {k\pi }{n}}={\frac {n}{\sin {\frac {\pi n}{2}}}}}$$

If n is an odd number (${\displaystyle n=2m+1}$) we can make use of the symmetries to get $${\displaystyle \prod _{k=1}^{m}\tan {\frac {k\pi }{2m+1}}={\sqrt {2m+1}}}$$

The transfer function of the Butterworth low pass filter can be expressed in terms of polynomial and poles. By setting the frequency as the cutoff frequency, the following identity can be proved: $${\displaystyle \prod _{k=1}^{n}\sin {\frac {\left(2k-1\right)\pi }{4n}}=\prod _{k=1}^{n}\cos {\frac {\left(2k-1\right)\pi }{4n}}={\frac {\sqrt {2}}{2^{n}}}}$$

Computing π

An efficient way to compute π to a large number of digits is based on the following identity without variables, due to Machin. This is known as a Machin-like formula: $${\displaystyle {\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}}$$ or, alternatively, by using an identity of Leonhard Euler: $${\displaystyle {\frac {\pi }{4}}=5\arctan {\frac {1}{7}}+2\arctan {\frac {3}{79}}}$$ or by using Pythagorean triples: $${\displaystyle \pi =\arccos {\frac {4}{5}}+\arccos {\frac {5}{13}}+\arccos {\frac {16}{65}}=\arcsin {\frac {3}{5}}+\arcsin {\frac {12}{13}}+\arcsin {\frac {63}{65}}.}$$

Others include: $${\displaystyle {\frac {\pi }{4}}=\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}},}$$ $${\displaystyle \pi =\arctan 1+\arctan 2+\arctan 3,}$$ $${\displaystyle {\frac {\pi }{4}}=2\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}.}$$

Generally, for numbers t₁, ..., t_n−1 ∈ (−1, 1) for which θ_n = Σ
_k=1 arctan t_k ∈ (π/4, 3π/4), let t_n = tan(π/2 − θ_n) = cot θ_n. This last expression can be computed directly using the formula for the cotangent of a sum of angles whose tangents are t₁, ..., t_n−1 and its value will be in (−1, 1). In particular, the computed t_n will be rational whenever all the t₁, ..., t_n−1 values are rational. With these values, $${\displaystyle {\begin{aligned}{\frac {\pi }{2}}&=\sum _{k=1}^{n}\arctan(t_{k})\\\pi &=\sum _{k=1}^{n}\operatorname {sgn}(t_{k})\arccos \left({\frac {1-t_{k}^{2}}{1+t_{k}^{2}}}\right)\\\pi &=\sum _{k=1}^{n}\arcsin \left({\frac {2t_{k}}{1+t_{k}^{2}}}\right)\\\pi &=\sum _{k=1}^{n}\arctan \left({\frac {2t_{k}}{1-t_{k}^{2}}}\right)\,,\end{aligned}}}$$

where in all but the first expression, we have used tangent half-angle formulae. The first two formulae work even if one or more of the t_k values is not within (−1, 1). Note that if t = p/q is rational, then the (2t, 1 − t, 1 + t) values in the above formulae are proportional to the Pythagorean triple (2pq, q − p, q + p).

For example, for n = 3 terms, $${\displaystyle {\frac {\pi }{2}}=\arctan \left({\frac {a}{b}}\right)+\arctan \left({\frac {c}{d}}\right)+\arctan \left({\frac {bd-ac}{ad+bc}}\right)}$$ for any a, b, c, d > 0.

An identity of Euclid

Euclid showed in Book XIII, Proposition 10 of his Elements that the area of the square on the side of a regular pentagon inscribed in a circle is equal to the sum of the areas of the squares on the sides of the regular hexagon and the regular decagon inscribed in the same circle. In the language of modern trigonometry, this says: $${\displaystyle \sin ^{2}18^{\circ }+\sin ^{2}30^{\circ }=\sin ^{2}36^{\circ }.}$$

Ptolemy used this proposition to compute some angles in his table of chords in Book I, chapter 11 of Almagest.

Composition of trigonometric functions

These identities involve a trigonometric function of a trigonometric function:

${\displaystyle \cos(t\sin x)=J_{0}(t)+2\sum _{k=1}^{\infty }J_{2k}(t)\cos(2kx)}$

${\displaystyle \sin(t\sin x)=2\sum _{k=0}^{\infty }J_{2k+1}(t)\sin {\big (}(2k+1)x{\big )}}$

${\displaystyle \cos(t\cos x)=J_{0}(t)+2\sum _{k=1}^{\infty }(-1)^{k}J_{2k}(t)\cos(2kx)}$

${\displaystyle \sin(t\cos x)=2\sum _{k=0}^{\infty }(-1)^{k}J_{2k+1}(t)\cos {\big (}(2k+1)x{\big )}}$

where J_i are Bessel functions.

Further "conditional" identities for the case α + β + γ = 180°

A conditional trigonometric identity is a trigonometric identity that holds if specified conditions on the arguments to the trigonometric functions are satisfied. The following formulae apply to arbitrary plane triangles and follow from ${\displaystyle \alpha +\beta +\gamma =180^{\circ },}$ as long as the functions occurring in the formulae are well-defined (the latter applies only to the formulae in which tangents and cotangents occur). $${\displaystyle {\begin{aligned}\tan \alpha +\tan \beta +\tan \gamma &=\tan \alpha \tan \beta \tan \gamma \\1&=\cot \beta \cot \gamma +\cot \gamma \cot \alpha +\cot \alpha \cot \beta \\\cot \left({\frac {\alpha }{2}}\right)+\cot \left({\frac {\beta }{2}}\right)+\cot \left({\frac {\gamma }{2}}\right)&=\cot \left({\frac {\alpha }{2}}\right)\cot \left({\frac {\beta }{2}}\right)\cot \left({\frac {\gamma }{2}}\right)\\1&=\tan \left({\frac {\beta }{2}}\right)\tan \left({\frac {\gamma }{2}}\right)+\tan \left({\frac {\gamma }{2}}\right)\tan \left({\frac {\alpha }{2}}\right)+\tan \left({\frac {\alpha }{2}}\right)\tan \left({\frac {\beta }{2}}\right)\\\sin \alpha +\sin \beta +\sin \gamma &=4\cos \left({\frac {\alpha }{2}}\right)\cos \left({\frac {\beta }{2}}\right)\cos \left({\frac {\gamma }{2}}\right)\\-\sin \alpha +\sin \beta +\sin \gamma &=4\cos \left({\frac {\alpha }{2}}\right)\sin \left({\frac {\beta }{2}}\right)\sin \left({\frac {\gamma }{2}}\right)\\\cos \alpha +\cos \beta +\cos \gamma &=4\sin \left({\frac {\alpha }{2}}\right)\sin \left({\frac {\beta }{2}}\right)\sin \left({\frac {\gamma }{2}}\right)+1\\-\cos \alpha +\cos \beta +\cos \gamma &=4\sin \left({\frac {\alpha }{2}}\right)\cos \left({\frac {\beta }{2}}\right)\cos \left({\frac {\gamma }{2}}\right)-1\\\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )&=4\sin \alpha \sin \beta \sin \gamma \\-\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )&=4\sin \alpha \cos \beta \cos \gamma \\\cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )&=-4\cos \alpha \cos \beta \cos \gamma -1\\-\cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )&=-4\cos \alpha \sin \beta \sin \gamma +1\\\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma &=2\cos \alpha \cos \beta \cos \gamma +2\\-\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma &=2\cos \alpha \sin \beta \sin \gamma \\\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma &=-2\cos \alpha \cos \beta \cos \gamma +1\\-\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma &=-2\cos \alpha \sin \beta \sin \gamma +1\\\sin ^{2}(2\alpha )+\sin ^{2}(2\beta )+\sin ^{2}(2\gamma )&=-2\cos(2\alpha )\cos(2\beta )\cos(2\gamma )+2\\\cos ^{2}(2\alpha )+\cos ^{2}(2\beta )+\cos ^{2}(2\gamma )&=2\cos(2\alpha )\,\cos(2\beta )\,\cos(2\gamma )+1\\1&=\sin ^{2}\left({\frac {\alpha }{2}}\right)+\sin ^{2}\left({\frac {\beta }{2}}\right)+\sin ^{2}\left({\frac {\gamma }{2}}\right)+2\sin \left({\frac {\alpha }{2}}\right)\,\sin \left({\frac {\beta }{2}}\right)\,\sin \left({\frac {\gamma }{2}}\right)\end{aligned}}}$$

Historical shorthands

Main articles: Versine and Exsecant

The versine, coversine, haversine, and exsecant were used in navigation. For example, the haversine formula was used to calculate the distance between two points on a sphere. They are rarely used today.

Miscellaneous

Dirichlet kernel

Main article: Dirichlet kernel

The Dirichlet kernel D_n(x) is the function occurring on both sides of the next identity: $${\displaystyle 1+2\cos x+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin \left({\frac {1}{2}}x\right)}}.}$$

The convolution of any integrable function of period ${\displaystyle 2\pi }$ with the Dirichlet kernel coincides with the function's ${\displaystyle n}$th-degree Fourier approximation. The same holds for any measure or generalized function.

Tangent half-angle substitution

Main article: Tangent half-angle substitution

If we set $${\displaystyle t=\tan {\frac {x}{2}},}$$ then $${\displaystyle \sin x={\frac {2t}{1+t^{2}}};\qquad \cos x={\frac {1-t^{2}}{1+t^{2}}};\qquad e^{ix}={\frac {1+it}{1-it}};\qquad dx={\frac {2\,dt}{1+t^{2}}},}$$ where ${\displaystyle e^{ix}=\cos x+i\sin x,}$ sometimes abbreviated to cis x.

When this substitution of ${\displaystyle t}$ for tan ⁠x/2⁠ is used in calculus, it follows that ${\displaystyle \sin x}$ is replaced by ⁠2t/1 + t⁠, ${\displaystyle \cos x}$ is replaced by ⁠1 − t/1 + t⁠ and the differential dx is replaced by ⁠2 dt/1 + t⁠. Thereby one converts rational functions of ${\displaystyle \sin x}$ and ${\displaystyle \cos x}$ to rational functions of ${\displaystyle t}$ in order to find their antiderivatives.

Viète's infinite product

See also: Viète's formula and Sinc function

$${\displaystyle \cos {\frac {\theta }{2}}\cdot \cos {\frac {\theta }{4}}\cdot \cos {\frac {\theta }{8}}\cdots =\prod _{n=1}^{\infty }\cos {\frac {\theta }{2^{n}}}={\frac {\sin \theta }{\theta }}=\operatorname {sinc} \theta .}$$

See also

• Aristarchus's inequality
• Derivatives of trigonometric functions
• Exact trigonometric values (values of sine and cosine expressed in surds)
• Exsecant
• Half-side formula
• Hyperbolic function
• Laws for solution of triangles:
  • Law of cosines
    • Spherical law of cosines
  • Law of sines
  • Law of tangents
  • Law of cotangents
  • Mollweide's formula
• List of integrals of trigonometric functions
• Mnemonics in trigonometry
• Pentagramma mirificum
• Proofs of trigonometric identities
• Prosthaphaeresis
• Pythagorean theorem
• Tangent half-angle formula
• Trigonometric number
• Trigonometry
• Uses of trigonometry
• Versine and haversine

References

1. Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) . "Chapter 4, eqn 4.3.45". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 73. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
2. Selby 1970, p. 188
3. Abramowitz and Stegun, p. 72, 4.3.13–15
4. Abramowitz and Stegun, p. 72, 4.3.7–9
5. Abramowitz and Stegun, p. 72, 4.3.16
6. ^ Weisstein, Eric W. "Trigonometric Addition Formulas". MathWorld.
7. Abramowitz and Stegun, p. 72, 4.3.17
8. Abramowitz and Stegun, p. 72, 4.3.18
9. ^ "Angle Sum and Difference Identities". www.milefoot.com. Retrieved 2019-10-12.
10. Abramowitz and Stegun, p. 72, 4.3.19
11. Abramowitz and Stegun, p. 80, 4.4.32
12. Abramowitz and Stegun, p. 80, 4.4.33
13. Abramowitz and Stegun, p. 80, 4.4.34
14. Bronstein, Manuel (1989). "Simplification of real elementary functions". In Gonnet, G. H. (ed.). Proceedings of the ACM-SIGSAM 1989 International Symposium on Symbolic and Algebraic Computation. ISSAC '89 (Portland US-OR, 1989-07). New York: ACM. pp. 207–211. doi:10.1145/74540.74566. ISBN 0-89791-325-6.
15. Michael Hardy. (2016). "On Tangents and Secants of Infinite Sums." The American Mathematical Monthly, volume 123, number 7, 701–703. https://doi.org/10.4169/amer.math.monthly.123.7.701
16. Hardy, Michael (2016). "On Tangents and Secants of Infinite Sums". American Mathematical Monthly. 123 (7): 701–703. doi:10.4169/amer.math.monthly.123.7.701.
17. ^ "Sine, Cosine, and Ptolemy's Theorem".
18. ^ Weisstein, Eric W. "Multiple-Angle Formulas". MathWorld.
19. Abramowitz and Stegun, p. 74, 4.3.48
20. ^ Selby 1970, pg. 190
21. Weisstein, Eric W. "Multiple-Angle Formulas". mathworld.wolfram.com. Retrieved 2022-02-06.
22. Ward, Ken. "Multiple angles recursive formula". Ken Ward's Mathematics Pages.
23. ^ Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) . "Chapter 4, eqn 4.3.20-22". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 72. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
24. ^ Weisstein, Eric W. "Half-Angle Formulas". MathWorld.
25. Abramowitz and Stegun, p. 72, 4.3.24–26
26. Weisstein, Eric W. "Double-Angle Formulas". MathWorld.
27. Abramowitz and Stegun, p. 72, 4.3.27–28
28. Abramowitz and Stegun, p. 72, 4.3.31–33
29. Eves, Howard (1990). An introduction to the history of mathematics (6th ed.). Philadelphia: Saunders College Pub. p. 309. ISBN 0-03-029558-0. OCLC 20842510.
30. Abramowitz and Stegun, p. 72, 4.3.34–39
31. Johnson, Warren P. (Apr 2010). "Trigonometric Identities à la Hermite". American Mathematical Monthly. 117 (4): 311–327. doi:10.4169/000298910x480784. S2CID 29690311.
32. "Product Identity Multiple Angle".
33. Apostol, T.M. (1967) Calculus. 2nd edition. New York, NY, Wiley. Pp 334-335.
34. ^ Weisstein, Eric W. "Harmonic Addition Theorem". MathWorld.
35. Ortiz Muñiz, Eddie (Feb 1953). "A Method for Deriving Various Formulas in Electrostatics and Electromagnetism Using Lagrange's Trigonometric Identities". American Journal of Physics. 21 (2): 140. Bibcode:1953AmJPh..21..140M. doi:10.1119/1.1933371.
36. Agarwal, Ravi P.; O'Regan, Donal (2008). Ordinary and Partial Differential Equations: With Special Functions, Fourier Series, and Boundary Value Problems (illustrated ed.). Springer Science & Business Media. p. 185. ISBN 978-0-387-79146-3. Extract of page 185
37. Jeffrey, Alan; Dai, Hui-hui (2008). "Section 2.4.1.6". Handbook of Mathematical Formulas and Integrals (4th ed.). Academic Press. ISBN 978-0-12-374288-9.
38. Fay, Temple H.; Kloppers, P. Hendrik (2001). "The Gibbs' phenomenon". International Journal of Mathematical Education in Science and Technology. 32 (1): 73–89. doi:10.1080/00207390117151.
39. Abramowitz and Stegun, p. 74, 4.3.47
40. Abramowitz and Stegun, p. 71, 4.3.2
41. Abramowitz and Stegun, p. 71, 4.3.1
42. Abramowitz and Stegun, p. 80, 4.4.26–31
43. Hawkins, Faith Mary; Hawkins, J. Q. (March 1, 1969). Complex Numbers and Elementary Complex Functions. London: MacDonald Technical & Scientific London (published 1968). p. 122. ISBN 978-0356025056.{{cite book}}: CS1 maint: date and year (link)
44. Markushevich, A. I. (1966). The Remarkable Sine Function. New York: American Elsevier Publishing Company, Inc. pp. 35–37, 81. ISBN 978-1483256313.
45. Abramowitz and Stegun, p. 74, 4.3.65–66
46. Abramowitz and Stegun, p. 75, 4.3.89–90
47. Abramowitz and Stegun, p. 85, 4.5.68–69
48. Abramowitz & Stegun 1972, p. 73, 4.3.45
49. ^ Wu, Rex H. "Proof Without Words: Euler's Arctangent Identity", Mathematics Magazine 77(3), June 2004, p. 189.
50. S. M. Abrarov, R. K. Jagpal, R. Siddiqui and B. M. Quine (2021), "Algorithmic determination of a large integer in the two-term Machin-like formula for π", Mathematics, 9 (17), 2162, arXiv:2107.01027, doi:10.3390/math9172162{{citation}}: CS1 maint: multiple names: authors list (link)
51. Humble, Steve (Nov 2004). "Grandma's identity". Mathematical Gazette. 88: 524–525. doi:10.1017/s0025557200176223. S2CID 125105552.
52. Weisstein, Eric W. "Sine". MathWorld.
53. Harris, Edward M. "Sums of Arctangents", in Roger B. Nelson, Proofs Without Words (1993, Mathematical Association of America), p. 39.
54. Milton Abramowitz and Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover Publications, New York, 1972, formulae 9.1.42–9.1.45
55. Er. K. C. Joshi, Krishna's IIT MATHEMATIKA. Krishna Prakashan Media. Meerut, India. page 636.
56. Abramowitz and Stegun, p. 72, 4.3.23

Bibliography

• Abramowitz, Milton; Stegun, Irene A., eds. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover Publications. ISBN 978-0-486-61272-0.
• Nielsen, Kaj L. (1966), Logarithmic and Trigonometric Tables to Five Places (2nd ed.), New York: Barnes & Noble, LCCN 61-9103
• Selby, Samuel M., ed. (1970), Standard Mathematical Tables (18th ed.), The Chemical Rubber Co.

External links

• Values of sin and cos, expressed in surds, for integer multiples of 3° and of ⁠5+5/8⁠°, and for the same angles csc and sec and tan

Categories:

• Mathematical identities
• Trigonometry
• Mathematics-related lists