Misplaced Pages

A joint Politics and Economics series
Social choice and electoral systems
Social choice Mechanism design Comparative politics Comparison List (By country)
Single-winner methodsSingle vote - plurality methods First preference plurality (FPP) Two-round (US: Jungle primary) Partisan primary Instant-runoff UK: Alternative vote (AV) US: Ranked-choice (RCV) Condorcet methods Condorcet-IRV Round-robin voting Minimax Schulze Ranked pairs Maximal lottery Positional voting Plurality (el. IRV) Borda count (el. Baldwin) Antiplurality (el. Coombs) Cardinal voting Score voting Approval voting Majority judgment STAR voting
Proportional representationParty-list Apportionment Highest averages Largest remainders National remnant Biproportional List type Closed list Open list Panachage List-free PR Localized list Quota-remainder methods Hare STV Schulze STV CPO-STV Quota Borda Approval-based committees Thiele's method Phragmen's method Expanding approvals rule Method of equal shares Fractional social choice Direct representation Interactive representation Liquid democracy Fractional approval voting Maximal lottery Random ballot Semi-proportional representation Cumulative SNTV Limited voting
Mixed systemsBy results of combination Mixed-member majoritarian Mixed-member proportional By mechanism of combination Non-compensatory Parallel (superposition) Coexistence Conditional Fusion (majority bonus) Compensatory Seat linkage system UK: 'AMS' NZ: 'MMP' Vote linkage system Negative vote transfer Mixed ballot Supermixed systems Dual-member proportional Rural–urban proportional Majority jackpot By ballot type Single vote Double simultaneous vote Dual-vote
Paradoxes and pathologiesSpoiler effects Spoiler effect Cloning paradox Frustrated majorities paradox Center squeeze Pathological response Perverse response Best-is-worst paradox No-show paradox Multiple districts paradox Strategic voting Lesser evil voting Exaggeration Truncation Turkey-raising Paradoxes of majority rule Tyranny of the majority Discursive dilemma Conflicting majorities paradox
Social and collective choiceImpossibility theorems Arrow's theorem Majority impossibility Moulin's impossibility theorem McKelvey–Schofield chaos theorem Gibbard's theorem Positive results Median voter theorem Condorcet's jury theorem May's theorem Condorcet dominance theorems Harsanyi's utilitarian theorem
Politics portal Economics portal Mathematics portal
v t e

In voting systems, the Minimax Condorcet method is a single-winner ranked-choice voting method that always elects the majority (Condorcet) winner. Minimax compares all candidates against each other in a round-robin tournament, then ranks candidates by their worst election result (the result where they would receive the fewest votes). The candidate with the largest (maximum) number of votes in their worst (minimum) matchup is declared the winner.

Description of the method

The Minimax Condorcet method selects the candidate for whom the greatest pairwise score for another candidate against him or her is the least such score among all candidates.

Football analogy

Imagine politicians compete like football teams in a round-robin tournament, where every team plays against every other team once. In each matchup, a candidate's score is equal to the number of voters who support them over their opponent.

Minimax finds each team's (or candidate's) worst game – the one where they received the smallest number of points (votes). Each team's tournament score is equal to the number of points they got in their worst game. The first place in the tournament goes to the team with the best tournament score.

Formal definition

Formally, let ${\displaystyle \operatorname {score} (X,Y)}$ denote the pairwise score for ${\displaystyle X}$ against ${\displaystyle Y}$. Then the candidate, ${\displaystyle W}$ selected by minimax (aka the winner) is given by:

${\displaystyle W=\arg \min _{X}\left(\max _{Y}\operatorname {score} (Y,X)\right)}$

Variants of the pairwise score

When it is permitted to rank candidates equally, or not rank all candidates, three interpretations of the rule are possible. When voters must rank all the candidates, all three variants are equivalent.

Let ${\displaystyle d(X,Y)}$ be the number of voters ranking X over Y. The variants define the score ${\displaystyle \operatorname {score} (X,Y)}$ for candidate X against Y as:

1. The number of voters ranking X above Y, but only when this score exceeds the number of voters ranking Y above X. If not, then the score for X against Y is zero. This variant is sometimes called winning votes is the most commonly used and preferred by social choice theorists.
   • ${\displaystyle \operatorname {score} (X,Y):={\begin{cases}d(X,Y),&d(X,Y)>d(Y,X)\\0,&{\text{else}}\end{cases}}}$
2. The number of voters ranking X above Y minus the number of voters ranking Y above X. This variant is called margins, and is less used.
   • ${\displaystyle \operatorname {score} (X,Y):=d(X,Y)-d(Y,X)}$
3. The number of voters ranking X above Y, regardless of whether more voters rank X above Y or vice versa. This variant is called pairwise opposition, and is also rarely used.
   • ${\displaystyle \operatorname {score} (X,Y):=d(X,Y)}$

When one of the first two variants is used, the method can be restated as: "Disregard the weakest pairwise defeat until one candidate is unbeaten." An "unbeaten" candidate possesses a maximum score against him which is zero or negative.

Satisfied and failed criteria

Minimax using winning votes or margins satisfies the Condorcet and the majority criterion, but not the Smith criterion, mutual majority criterion, or Condorcet loser criterion. When winning votes is used, minimax also satisfies the plurality criterion.

Minimax fails independence of irrelevant alternatives, independence of clones, local independence of irrelevant alternatives, and independence of Smith-dominated alternatives.

With the pairwise opposition variant (sometimes called MMPO), minimax only satisfies the majority-strength Condorcet criterion; a candidate with a relative majority over every other may not be elected. MMPO is a later-no-harm system and also satisfies sincere favorite criterion.

Nicolaus Tideman modified minimax to only drop edges that create Condorcet cycles, allowing his method to satisfy many of the above properties. Schulze's method similarly reduces to minimax when there are only three candidates.

Examples

Example with Condorcet winner

• v
• t
• e

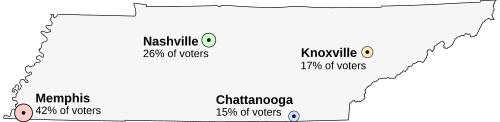
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:

• Memphis, the largest city, but far from the others (42% of voters)
• Nashville, near the center of the state (26% of voters)
• Chattanooga, somewhat east (15% of voters)
• Knoxville, far to the northeast (17% of voters)

The preferences of each region's voters are:

The results of the pairwise scores would be tabulated as follows:

• indicates voters who preferred the candidate listed in the column caption to the candidate listed in the row caption
• indicates voters who preferred the candidate listed in the row caption to the candidate listed in the column caption

Result: In all three alternatives Nashville has the lowest value and is elected winner.

Example with Condorcet winner that is not elected winner (for pairwise opposition)

Assume three candidates A, B and C and voters with the following preferences:

The results would be tabulated as follows:

• indicates voters who preferred the candidate listed in the column caption to the candidate listed in the row caption
• indicates voters who preferred the candidate listed in the row caption to the candidate listed in the column caption

Result: With the winning votes and margins alternatives, the Condorcet winner A is declared Minimax winner. However, using the pairwise opposition alternative, C is declared winner, since less voters strongly oppose him in his worst pairwise score against A than A is opposed by in his worst pairwise score against B.

Example without Condorcet winner

Assume four candidates A, B, C and D. Voters are allowed to not consider some candidates (denoting an n/a in the table), so that their ballots are not taken into account for pairwise scores of that candidates.

The results would be tabulated as follows:

• indicates voters who preferred the candidate listed in the column caption to the candidate listed in the row caption
• indicates voters who preferred the candidate listed in the row caption to the candidate listed in the column caption

Result: Each of the three alternatives gives another winner:

• the winning votes alternative chooses A as winner, since it has the lowest value of 35 votes for the winner in his biggest defeat;
• the margin alternative chooses B as winner, since it has the lowest difference of votes in his biggest defeat;
• and pairwise opposition chooses the Condorcet loser D as winner, since it has the lowest votes of the biggest opponent in all pairwise scores.

See also

• Minimax – main minimax article
• Multiwinner voting – contains information on some multiwinner variants of Minimax Condorcet.

References

1. "[EM] the name of the rose". lists.electorama.com. Retrieved 2024-02-12.

• Levin, Jonathan, and Barry Nalebuff. 1995. "An Introduction to Vote-Counting Schemes." Journal of Economic Perspectives, 9(1): 3–26.

External links

• Description of ranked ballot voting methods: Simpson by Rob LeGrand
• Condorcet Class PHP library supporting multiple Condorcet methods, including the three variants of Minimax method.
• Electowiki: minmax

• Monotonic Condorcet methods