| Revision as of 15:48, 13 August 2022 view sourceAlgebraicLandScape (talk | contribs)1 edit →Conjectures, problems and hypotheses: The second to last bullet point had “exactly one” repeated twice.Tags: Mobile edit Mobile web edit← Previous edit | Revision as of 02:05, 17 August 2022 view source Duckmather (talk | contribs)Extended confirmed users9,195 edits remove unnecessary "Conjectures and problems", "Open questions", "Other", etc headers; copy-edit (and LaTeXify) for clarity; expand/cleanup refs; added {{Duplication}}Tag: Visual editNext edit → | ||
| Line 1: | Line 1: | ||
| {{Short description| |
{{Short description|List article of unsolved mathematical problems}} | ||
| {{Dynamic list}} | {{Dynamic list}} | ||
| Many ] have not yet |
Many ] have been stated but not yet solved. These problems come from many ], such as ], ], ], ], ], ], ], ] and ], ], ], ], ], ], ], ]s, and ]s. Some problems belong to more than one discipline and are studied using techniques from different areas. Prizes are often awarded for the solution to a long-standing problem, and some lists of unsolved problems, such as the ], receive considerable attention. | ||
| This |
This list is a composite of notable unsolved problems mentioned in previously published lists, including but not limited to lists considered authoritative. Although this list may never be comprehensive, the problems listed here vary widely in both difficulty and importance. | ||
| == Lists of unsolved problems in mathematics == | == Lists of unsolved problems in mathematics == | ||
| Line 11: | Line 12: | ||
| {| class="wikitable sortable" | {| class="wikitable sortable" | ||
| |- | |- | ||
| ! List !! Number of<br />problems !! Number |
! List !! Number of<br />problems !! Number unsolved <br /> or incompletely solved !! Proposed by !! Proposed<br />in | ||
| |- | |- | ||
| | ]<ref>{{citation|last=Thiele|first=Rüdiger|chapter=On Hilbert and his twenty-four problems|title=Mathematics and the historian's craft. The Kenneth O. May Lectures|pages=243–295|isbn=978-0-387-25284-1|editor-last=Van Brummelen|editor-first=Glen|year=2005|series=] Books in Mathematics/Ouvrages de Mathématiques de la SMC|volume=21|title-link=Kenneth May}}</ref> || 23 || 15 || ] || 1900 | | ]<ref>{{citation|last=Thiele|first=Rüdiger|chapter=On Hilbert and his twenty-four problems|title=Mathematics and the historian's craft. The Kenneth O. May Lectures|pages=243–295|isbn=978-0-387-25284-1|editor-last=Van Brummelen|editor-first=Glen|year=2005|series=] Books in Mathematics/Ouvrages de Mathématiques de la SMC|volume=21|title-link=Kenneth May}}</ref> || 23 || 15 || ] || 1900 | ||
| Line 43: | Line 44: | ||
| | ] || 18 || 14 || ] || 1998 | | ] || 18 || 14 || ] || 1998 | ||
| |- | |- | ||
| | ] || 7 || 6<ref name="auto1">{{cite web|url=http://claymath.org/millennium-problems |
| ] || 7 || 6<ref name="auto1">{{cite web |title=Millennium Problems |url=http://claymath.org/millennium-problems |url-status=dead |archive-url=https://web.archive.org/web/20170606121331/http://claymath.org/millennium-problems |archive-date=2017-06-06 |access-date=2015-01-20 |website=claymath.org}}</ref>|| ] || 2000 | ||
| |- | |- | ||
| | ] || 15 || <12<ref>{{cite web |url=http://www2.cnrs.fr/en/2435.htm?debut=8&theme1=12 |title=Fields Medal awarded to Artur Avila |website=] |date=2014-08-13 |access-date=2018-07-07 |archive-url=https://web.archive.org/web/20180710010437/http://www2.cnrs.fr/en/2435.htm?debut=8&theme1=12 |archive-date=2018-07-10 |url-status=dead }}</ref><ref name="guardian">{{cite web |url=https://www.theguardian.com/science/alexs-adventures-in-numberland/2014/aug/13/fields-medals-2014-maths-avila-bhargava-hairer-mirzakhani |title=Fields Medals 2014: the maths of Avila, Bhargava, Hairer and Mirzakhani explained |website=] |last=Bellos |first=Alex |date=2014-08-13 |access-date=2018-07-07 |archive-url=https://web.archive.org/web/20161021115900/https://www.theguardian.com/science/alexs-adventures-in-numberland/2014/aug/13/fields-medals-2014-maths-avila-bhargava-hairer-mirzakhani |archive-date=2016-10-21 |url-status=live }}</ref> || ] || 2000 | | ] || 15 || <12<ref>{{cite web |url=http://www2.cnrs.fr/en/2435.htm?debut=8&theme1=12 |title=Fields Medal awarded to Artur Avila |website=] |date=2014-08-13 |access-date=2018-07-07 |archive-url=https://web.archive.org/web/20180710010437/http://www2.cnrs.fr/en/2435.htm?debut=8&theme1=12 |archive-date=2018-07-10 |url-status=dead }}</ref><ref name="guardian">{{cite web |url=https://www.theguardian.com/science/alexs-adventures-in-numberland/2014/aug/13/fields-medals-2014-maths-avila-bhargava-hairer-mirzakhani |title=Fields Medals 2014: the maths of Avila, Bhargava, Hairer and Mirzakhani explained |website=] |last=Bellos |first=Alex |date=2014-08-13 |access-date=2018-07-07 |archive-url=https://web.archive.org/web/20161021115900/https://www.theguardian.com/science/alexs-adventures-in-numberland/2014/aug/13/fields-medals-2014-maths-avila-bhargava-hairer-mirzakhani |archive-date=2016-10-21 |url-status=live }}</ref> || ] || 2000 | ||
| Line 49: | Line 50: | ||
| | Unsolved Problems on Mathematics for the 21st Century<ref>{{cite book | last1 = Abe | first1 = Jair Minoro | last2 = Tanaka | first2 = Shotaro | title = Unsolved Problems on Mathematics for the 21st Century | publisher = IOS Press | year = 2001 | url = https://books.google.com/books?id=yHzfbqtVGLIC&q=unsolved+problems+in+mathematics | isbn = 978-9051994902}}</ref> || 22 || - || Jair Minoro Abe, Shotaro Tanaka || 2001 | | Unsolved Problems on Mathematics for the 21st Century<ref>{{cite book | last1 = Abe | first1 = Jair Minoro | last2 = Tanaka | first2 = Shotaro | title = Unsolved Problems on Mathematics for the 21st Century | publisher = IOS Press | year = 2001 | url = https://books.google.com/books?id=yHzfbqtVGLIC&q=unsolved+problems+in+mathematics | isbn = 978-9051994902}}</ref> || 22 || - || Jair Minoro Abe, Shotaro Tanaka || 2001 | ||
| |- | |- | ||
| | DARPA's math challenges<ref>{{cite web | title = DARPA invests in math | publisher = ] | date = 2008-10-14 | url = http://edition.cnn.com/2008/TECH/science/10/09/darpa.challenges/index.html | access-date = 2013-01-14 | archive-url = https://web.archive.org/web/20090304121240/http://edition.cnn.com/2008/TECH/science/10/09/darpa.challenges/index.html | archive-date = 2009-03-04}}</ref><ref>{{cite web | title = Broad Agency Announcement (BAA 07-68) for Defense Sciences Office (DSO) | publisher = DARPA | date = 2007-09-10 | url = http://www.math.utk.edu/~vasili/refs/darpa07.MathChallenges.html | access-date = 2013-06-25 | archive-url = https://web.archive.org/web/20121001111057/http://www.math.utk.edu/~vasili/refs/darpa07.MathChallenges.html | | ]'s math challenges<ref>{{cite web | title = DARPA invests in math | publisher = ] | date = 2008-10-14 | url = http://edition.cnn.com/2008/TECH/science/10/09/darpa.challenges/index.html | access-date = 2013-01-14 | archive-url = https://web.archive.org/web/20090304121240/http://edition.cnn.com/2008/TECH/science/10/09/darpa.challenges/index.html | archive-date = 2009-03-04}}</ref><ref>{{cite web | title = Broad Agency Announcement (BAA 07-68) for Defense Sciences Office (DSO) | publisher = DARPA | date = 2007-09-10 | url = http://www.math.utk.edu/~vasili/refs/darpa07.MathChallenges.html | access-date = 2013-06-25 | archive-url = https://web.archive.org/web/20121001111057/http://www.math.utk.edu/~vasili/refs/darpa07.MathChallenges.html | ||
| | archive-date = 2012-10-01}}</ref> || 23 || - || ] || 2007 | | archive-date = 2012-10-01}}</ref> || 23 || - || ] || 2007 | ||
| |} | |} | ||
| Line 55: | Line 56: | ||
| === Millennium Prize Problems === | === Millennium Prize Problems === | ||
| Of the original seven ] set by the ] in 2000, six |
Of the original seven ] set by the ] in 2000, six remain unsolved:<ref name="auto1"/> | ||
| * ] | * ] | ||
| Line 64: | Line 65: | ||
| * ] | * ] | ||
| The seventh problem, the ], |
The seventh problem, the ], was solved by ] in 2003.<ref>{{cite web |title=Poincaré Conjecture |url=http://www.claymath.org/millenium-problems/poincar%C3%A9-conjecture |archive-url=https://web.archive.org/web/20131215120130/http://www.claymath.org/millenium-problems/poincar%C3%A9-conjecture |archive-date=2013-12-15 |website=Clay Mathematics Institute}}</ref> However, a generalization called the ]—that is, whether a ''four''-dimensional topological sphere can have two or more inequivalent ]s—is unsolved.<ref>{{cite web |title=Smooth 4-dimensional Poincare conjecture |url=http://www.openproblemgarden.org/?q=op/smooth_4_dimensional_poincare_conjecture |url-status=live |archive-url=https://web.archive.org/web/20180125203721/http://www.openproblemgarden.org/?q=op%2Fsmooth_4_dimensional_poincare_conjecture |archive-date=2018-01-25 |access-date=2019-08-06 |website=Open Problem Garden}}</ref> | ||
| == Unsolved problems == | == Unsolved problems == | ||
| Line 72: | Line 73: | ||
| ] representation of a ], a ] forms a ]. Zauner conjectured that analogous structures exist in complex ]s of all finite dimensions.]] | ] representation of a ], a ] forms a ]. Zauner conjectured that analogous structures exist in complex ]s of all finite dimensions.]] | ||
| ====Notebook problems==== | |||
| * The Dniester Notebook (''Dnestrovskaya Tetrad'') collects several hundred unresolved problems in algebra, particularly ] and ].<ref>{{citation|year=1993|title=Dnestrovskaya notebook|publisher=The Russian Academy of Sciences|language=ru |url=http://math.nsc.ru/LBRT/a1/files/dnestr93.pdf}}<br />{{citation |url=https://math.usask.ca/~bremner/research/publications/dniester.pdf |title=Dniester Notebook: Unsolved Problems in the Theory of Rings and Modules |website=] |access-date=2019-08-15}}</ref> | |||
| * The Erlagol Notebook (''Erlagolskaya Tetrad'') collects unresolved problems in algebra and model theory.<ref>{{citation|year=2018|title=Erlagol notebook|publisher=The Novosibirsk State University|language=ru |url=http://uamt.conf.nstu.ru/erl_note.pdf}}</ref> | |||
| ====Conjectures and problems==== | |||
| * ] on the relation between the order of the ] of the ] of the ] of a ] to the field's ]. | * ] on the relation between the order of the ] of the ] of the ] of a ] to the field's ]. | ||
| * ]s on densities of rational points of ]s and ] defined on ] and their ]s. | * ]s on densities of rational points of ]s and ] defined on ] and their ]s. | ||
| * ] in ] theory |
* ] in ] theory | ||
| * ] |
* ]: the ] of a complex function <math>f</math> applied to a complex matrix <math>A</math> is at most twice the ] of <math>|f(z)|</math> over the ] of <math>A</math>. | ||
| * ] on ]s of ]s over the integers. | * ] on ]s of ]s over the integers. | ||
| * ] |
* ]: a group with ] 2 also has a 2-dimensional ] <math>K(G, 1)</math>. | ||
| * ] on whether certain ]s are ]. | * ] on whether certain ]s are ]. | ||
| ** ] |
** ]. a specific case of the Farrell–Jones conjecture | ||
| * ]:<ref>{{cite journal |last1=Dowling |first1=T. A. |title=A class of geometric lattices based on finite groups|journal=] |series=Series B |date=February 1973 |volume=14 |issue=1 |pages=61–86 |doi=10.1016/S0095-8956(73)80007-3 | doi-access=free }}</ref> |
* ]: is every finite ] isomorphic to the ] of some finite ]?<ref>{{cite journal |last1=Dowling |first1=T. A. |title=A class of geometric lattices based on finite groups|journal=] |series=Series B |date=February 1973 |volume=14 |issue=1 |pages=61–86 |doi=10.1016/S0095-8956(73)80007-3 | doi-access=free }}</ref> | ||
| * ] |
* ]: the ] of a non-] is determined by the extent to which it, as a ], has ]. | ||
| * ] | * ] | ||
| * ]: for every positive integer <math>k</math>, a ] of order <math>4k</math> exists. | * ]: for every positive integer <math>k</math>, a ] of order <math>4k</math> exists. | ||
| * ]: what is the largest ] of a matrix with entries all equal to 1 or |
* ]: what is the largest ] of a matrix with entries all equal to 1 or –1? | ||
| * ]: put ] on a rigorous foundation. | * ]: put ] on a rigorous foundation. | ||
| * ]: what are the possible configurations of the ] of ]? | * ]: what are the possible configurations of the ] of ]? | ||
| * ] | * ] | ||
| * ] |
* ]: the intersection of all powers of the ] of a left-and-right ] is precisely 0. | ||
| * ] | * ] | ||
| * ] |
* ]: if a ring has no ] other than <math>\{0\}</math>, then it has no nil ] other than <math>\{0\}</math>. | ||
| * Existence of ]s and associated ] | * Existence of ]s and associated ] | ||
| * ] |
* ]: every piecewise-polynomial <math>f:\mathbb{R}^{n}\rightarrow\mathbb{R}</math> is the maximum of a finite set of minimums of finite collections of polynomials. | ||
| * ] |
* ]: for matroids of rank <math>n</math> with <math>n</math> disjoint bases <math>B_{i}</math>, it is possible to create an <math>n \times n</math> matrix whose rows are <math>B_{i}</math> and whose columns are also bases. | ||
| * ] |
* ]: if a complex polynomial with degree at least <math>2</math> has all roots in the closed ], then each root is within distance <math>1</math> from some ]. | ||
| * ] |
* ]: if <math>G</math> is a ] ] over a perfect ] of ] at most <math>2</math>, then the ] set <math>H^{1}(F, G)</math> is zero. | ||
| * ] | * ] | ||
| * ]: ]s of ] <math>g \geq 2</math> over ] <math>K</math> have at most some bounded number <math>N(K, g)</math> of <math>K</math>-]s |
* ]: do ]s of ] <math>g \geq 2</math> over ] <math>K</math> have at most some bounded number <math>N(K, g)</math> of <math>K</math>-]s? | ||
| * ]: classification of pairs of |
* ]: classification of pairs of <math>n\times n</math> matrices under simultaneous conjugation and problems containing it such as a lot of classification problems | ||
| * ] |
* ]: for a ] <math>V</math> with ] <math>R</math>, if the ] of <math>R</math> are a ] over <math>R</math>, then <math>V</math> is ]. | ||
| * Zauner's conjecture |
* Zauner's conjecture: do ]s exist in all dimensions? | ||
| ==== Notebook problems ==== | |||
| * The Dniester Notebook ({{Lang-ru|Днестровская тетрадъ}}) lists several hundred unsolved problems in algebra, particularly ] and ].<ref>* {{citation |title=ДНЕСТРОВСКАЯ ТЕТРАДЪ |url=http://math.nsc.ru/LBRT/a1/files/dnestr93.pdf |year=1993 |trans-title=DNIESTER NOTEBOOK |publisher=The Russian Academy of Sciences |language=ru}} | |||
| * {{citation |title=Dniester Notebook: Unsolved Problems in the Theory of Rings and Modules |url=https://math.usask.ca/~bremner/research/publications/dniester.pdf |website=] |access-date=2019-08-15}}</ref> | |||
| * The Erlagol Notebook ({{Lang-ru|Эрлаголъская тетрадъ}}) lists unsolved problems in algebra and model theory.<ref>{{citation |title=Эрлаголъская тетрадъ |url=http://uamt.conf.nstu.ru/erl_note.pdf |year=2018 |trans-title=Erlagol notebook |publisher=The Novosibirsk State University |language=ru}}</ref> | |||
| === Analysis === | === Analysis === | ||
| {{Main|Mathematical analysis}} | {{Main|Mathematical analysis}} | ||
| ], which may or may not be a rational number.]] | ], which may or may not be a rational number.]] | ||
| * The ]: estimating the integral of powers of the moduli of the derivative of ]s into the open unit disk, on certain subsets of <math>\mathbb{C}</math> | |||
| ====Conjectures and problems==== | |||
| * The ]: the transcendence of at least one of four exponentials of combinations of irrationals<ref name=waldschmidt>{{citation|pages=14, 16|url=https://books.google.com/books?id=Wrj0CAAAQBAJ&pg=PA14|title=Diophantine Approximation on Linear Algebraic Groups: Transcendence Properties of the Exponential Function in Several Variables|first=Michel|last=Waldschmidt|publisher=Springer|year=2013|isbn=9783662115695}}</ref> | |||
| * The ] on estimating the integral of powers of the moduli of the derivative of ]s into the open unit disk, on certain subsets of <math>\mathbb{C}</math> | |||
| * The ] on the transcendence of at least one of four exponentials of combinations of irrationals<ref name=waldschmidt>{{citation|pages=14, 16|url=https://books.google.com/books?id=Wrj0CAAAQBAJ&pg=PA14|title=Diophantine Approximation on Linear Algebraic Groups: Transcendence Properties of the Exponential Function in Several Variables|first=Michel|last=Waldschmidt|publisher=Springer|year=2013|isbn=9783662115695}}</ref> | |||
| * ] on the coefficients of ]s | * ] on the coefficients of ]s | ||
| * ] – does every ] on a complex ] send some non-trivial ] subspace to itself? | * ] – does every ] on a complex ] send some non-trivial ] subspace to itself? | ||
| Line 121: | Line 121: | ||
| * ] on compact subsets of <math>\mathbb{C}</math> with analytic capacity <math>0</math> | * ] on compact subsets of <math>\mathbb{C}</math> with analytic capacity <math>0</math> | ||
| * Are <math>\gamma</math> (the ]),<math>\pi + e, \pi - e, \pi e, \pi/e, \pi^e, \pi^{\sqrt{2}}, \pi^{\pi}, e^{\pi^2}, \ln\pi, 2^e, e^e</math>, ], or ] rational, ] irrational, or ]? What is the ] of each of these numbers?<ref>For some background on the numbers in this problem, see articles by ] at ] (all articles accessed 15 December 2014): | |||
| ====Open questions==== | |||
| * Are <math>\gamma</math> (the ]), ] + '']'', {{pi}} − ''e'', {{pi}}''e'', {{pi}}/''e'', {{pi}}<sup>''e''</sup>, {{pi}}<sup>]</sup>, {{pi}}<sup>{{pi}}</sup>, ''e''<sup>{{pi}}<sup>2</sup></sup>, ] {{pi}}, 2<sup>''e''</sup>, ''e''<sup>''e''</sup>, ], or ]; rational, ] irrational, or ]? What is the ] of each of these numbers?<ref>For background on the numbers that are the focus of this problem, see articles by Eric W. Weisstein, on pi ( {{Webarchive|url=https://web.archive.org/web/20141206023912/http://mathworld.wolfram.com/Pi.html |date=2014-12-06 }}), e ( {{Webarchive|url=https://web.archive.org/web/20141121122615/http://mathworld.wolfram.com/e.html |date=2014-11-21 }}), Khinchin's Constant ( {{Webarchive|url=https://web.archive.org/web/20141105201509/http://mathworld.wolfram.com/KhinchinsConstant.html |date=2014-11-05 }}), irrational numbers ( {{Webarchive|url=https://web.archive.org/web/20150327024040/http://mathworld.wolfram.com/IrrationalNumber.html |date=2015-03-27 }}), transcendental numbers ( {{Webarchive|url=https://web.archive.org/web/20141113174913/http://mathworld.wolfram.com/TranscendentalNumber.html |date=2014-11-13 }}), and irrationality measures ( {{Webarchive|url=https://web.archive.org/web/20150421203736/http://mathworld.wolfram.com/IrrationalityMeasure.html |date=2015-04-21 }}) at Wolfram ''MathWorld'', all articles accessed 15 December 2014.</ref><ref>Michel Waldschmidt, 2008, "An introduction to irrationality and transcendence methods," at The University of Arizona The Southwest Center for Arithmetic Geometry 2008 Arizona Winter School, March 15–19, 2008 (Special Functions and Transcendence), see {{Webarchive|url=https://web.archive.org/web/20141216004531/http://webusers.imj-prg.fr/~michel.waldschmidt/articles/pdf/AWSLecture5.pdf |date=2014-12-16 }}, accessed 15 December 2014.</ref><ref>John Albert, posting date unknown, "Some unsolved problems in number theory" , in University of Oklahoma Math 4513 course materials, see {{Webarchive|url=https://web.archive.org/web/20140117150133/http://www2.math.ou.edu/~jalbert/courses/openprob2.pdf |date=2014-01-17 }}, accessed 15 December 2014.</ref> | |||
| * ({{Webarchive|url=https://web.archive.org/web/20141206023912/http://mathworld.wolfram.com/Pi.html|date=2014-12-06}}) | |||
| * ({{Webarchive|url=https://web.archive.org/web/20141121122615/http://mathworld.wolfram.com/e.html|date=2014-11-21}}) | |||
| * ({{Webarchive|url=https://web.archive.org/web/20141105201509/http://mathworld.wolfram.com/KhinchinsConstant.html|date=2014-11-05}}) | |||
| * ({{Webarchive|url=https://web.archive.org/web/20150327024040/http://mathworld.wolfram.com/IrrationalNumber.html|date=2015-03-27}}) | |||
| * ({{Webarchive|url=https://web.archive.org/web/20141113174913/http://mathworld.wolfram.com/TranscendentalNumber.html|date=2014-11-13}}) | |||
| * ({{Webarchive|url=https://web.archive.org/web/20150421203736/http://mathworld.wolfram.com/IrrationalityMeasure.html|date=2015-04-21}})</ref><ref>{{Cite conference |last=Waldschmidt |first=Michel |date=2008 |title=An introduction to irrationality and transcendence methods. |url=https://webusers.imj-prg.fr/~michel.waldschmidt/articles/pdf/AWSLecture5.pdf |conference=2008 Arizona Winter School |archive-url=https://web.archive.org/web/20141216004531/http://webusers.imj-prg.fr/~michel.waldschmidt/articles/pdf/AWSLecture5.pdf |archive-date=16 December 2014 |access-date=15 December 2014}}</ref><ref>{{Citation |last=Albert |first=John |title=Some unsolved problems in number theory |url=http://www2.math.ou.edu/~jalbert/courses/openprob2.pdf |archive-url=https://web.archive.org/web/20140117150133/http://www2.math.ou.edu/~jalbert/courses/openprob2.pdf |access-date=15 December 2014 |archive-date=17 December 2014}}</ref> | |||
| * What is the exact value of ], including ]? | * What is the exact value of ], including ]? | ||
| * How are suspended infinite-infinitesimals paradoxes justified? | * How are suspended infinite-infinitesimals paradoxes justified? | ||
| ====Other==== | |||
| * Regularity of solutions of ] | * Regularity of solutions of ] | ||
| * Convergence of ] | * Convergence of ] | ||
| Line 132: | Line 137: | ||
| === Combinatorics === | === Combinatorics === | ||
| {{Main|Combinatorics}} |
{{Main|Combinatorics}} | ||
| ====Conjectures and problems==== | |||
| * The ] – does every finite ] that is not ] contain two elements ''x'' and ''y'' such that the probability that ''x'' appears before ''y'' in a random ] is between 1/3 and 2/3?<ref>{{citation | * The ] – does every finite ] that is not ] contain two elements ''x'' and ''y'' such that the probability that ''x'' appears before ''y'' in a random ] is between 1/3 and 2/3?<ref>{{citation | ||
| | last1 = Brightwell | first1 = Graham R. | | last1 = Brightwell | first1 = Graham R. | ||
| Line 183: | Line 187: | ||
| }}</ref> | }}</ref> | ||
| ====Other==== | |||
| * The values of the ]s <math>M(n)</math> for <math>n \ge 9</math>.<ref>{{Cite web |url=http://www.sfu.ca/~tyusun/ThesisDedekind.pdf |title=Dedekind Numbers and Related Sequences |access-date=2020-04-30 |archive-date=2015-03-15 |archive-url=https://web.archive.org/web/20150315021125/http://www.sfu.ca/~tyusun/ThesisDedekind.pdf |url-status=dead }}</ref> | * The values of the ]s <math>M(n)</math> for <math>n \ge 9</math>.<ref>{{Cite web |url=http://www.sfu.ca/~tyusun/ThesisDedekind.pdf |title=Dedekind Numbers and Related Sequences |access-date=2020-04-30 |archive-date=2015-03-15 |archive-url=https://web.archive.org/web/20150315021125/http://www.sfu.ca/~tyusun/ThesisDedekind.pdf |url-status=dead }}</ref> | ||
| * Give a combinatorial interpretation of the ]s.<ref>{{citation | * Give a combinatorial interpretation of the ]s.<ref>{{citation | ||
| Line 205: | Line 208: | ||
| {{Main|Dynamical system}} | {{Main|Dynamical system}} | ||
| ]. It is not known whether the Mandelbrot set is ] or not.]] | ]. It is not known whether the Mandelbrot set is ] or not.]] | ||
| ====Conjectures and problems==== | |||
| * ] and ] – relating symplectic geometry to Morse theory | * ] and ] – relating symplectic geometry to Morse theory | ||
| * ] | * ] | ||
| * ] problem – is there an ] with simple Lebesgue spectrum?<ref>S. M. Ulam, Problems in Modern Mathematics. Science Editions John Wiley & Sons, Inc., New York, 1964, page 76.</ref> | * ] problem – is there an ] with simple Lebesgue spectrum?<ref>S. M. Ulam, Problems in Modern Mathematics. Science Editions John Wiley & Sons, Inc., New York, 1964, page 76.</ref> | ||
| * ] conjecture – if a ] is strictly convex and integrable, is its boundary necessarily an ellipse?<ref>{{cite journal |last1=Kaloshin |first1=Vadim |author-link1=Vadim Kaloshin |last2=Sorrentino |first2=Alfonso |title=On the local Birkhoff conjecture for convex billiards |doi=10.4007/annals.2018.188.1.6 |volume=188 |number=1 |year=2018 |pages=315–380 |journal=]|arxiv=1612.09194 |s2cid=119171182 }}</ref> | * ] conjecture – if a ] is strictly convex and integrable, is its boundary necessarily an ellipse?<ref>{{cite journal |last1=Kaloshin |first1=Vadim |author-link1=Vadim Kaloshin |last2=Sorrentino |first2=Alfonso |title=On the local Birkhoff conjecture for convex billiards |doi=10.4007/annals.2018.188.1.6 |volume=188 |number=1 |year=2018 |pages=315–380 |journal=]|arxiv=1612.09194 |s2cid=119171182 }}</ref> | ||
| * ] ( |
* ] (''aka'' the <math>3n + 1</math> conjecture) | ||
| * ] conjecture |
* ] conjecture: every component of the ] of an ] ] function is unbounded | ||
| * ] conjecture – is every invariant and ] measure for the <math>\times 2,\times 3</math> action on the circle either Lebesgue or atomic? | * ] conjecture – is every invariant and ] measure for the <math>\times 2,\times 3</math> action on the circle either Lebesgue or atomic? | ||
| * ] on the dimension of an ] in terms of its ]s | * ] on the dimension of an ] in terms of its ]s | ||
| Line 221: | Line 223: | ||
| * ] – does a regular compact ] ] of a ] on a ] carry at least one periodic orbit of the Hamiltonian flow? | * ] – does a regular compact ] ] of a ] on a ] carry at least one periodic orbit of the Hamiltonian flow? | ||
| ====Open questions==== | |||
| * Does every positive integer generate a ] terminating at 1? | * Does every positive integer generate a ] terminating at 1? | ||
| * ] – For what classes of ], describing dynamical systems, does the Lyapunov’s second method formulated in the classical and canonically generalized forms define the necessary and sufficient conditions for the (asymptotical) stability of motion? | * ] – For what classes of ], describing dynamical systems, does the Lyapunov’s second method formulated in the classical and canonically generalized forms define the necessary and sufficient conditions for the (asymptotical) stability of motion? | ||
| * Is every ] in three or more dimensions locally reversible?<ref>{{cite conference |last=Kari |first=Jarkko |author-link=Jarkko Kari |year=2009 |title=Structure of Reversible Cellular Automata |conference=International Conference on Unconventional Computation |series=] |publisher=Springer |volume=5715 |page=6 |bibcode=2009LNCS.5715....6K |doi=10.1007/978-3-642-03745-0_5 |isbn=978-3-642-03744-3 |doi-access=free |contribution=Structure of reversible cellular automata}}</ref> | |||
| * Is every ] in three or more dimensions locally reversible?<ref>{{citation | |||
| | last = Kari | first = Jarkko | author-link = Jarkko Kari | |||
| | contribution = Structure of reversible cellular automata | |||
| | doi = 10.1007/978-3-642-03745-0_5 | |||
| | page = 6 | |||
| | publisher = Springer | |||
| | series = ] | |||
| | title = Unconventional Computation: 8th International Conference, UC 2009, Ponta Delgada, Portugal, September 7ÔÇô11, 2009, Proceedings | |||
| | volume = 5715 | |||
| | year = 2009| bibcode = 2009LNCS.5715....6K| isbn = 978-3-642-03744-3 | doi-access = free | |||
| }}</ref> | |||
| === Games and puzzles === | === Games and puzzles === | ||
| Line 258: | Line 249: | ||
| ==== Algebraic geometry ==== | ==== Algebraic geometry ==== | ||
| {{Main|Algebraic geometry}} | {{Main|Algebraic geometry}} | ||
| * ]: if the ] of a ] with ] is ], then it is semiample. | |||
| =====Conjectures===== | |||
| * ] that if the ] of a ] with ] is ], then it is semiample. | |||
| * ] on the ] of certain ]. | * ] on the ] of certain ]. | ||
| * ]: any one of numerous named for ]. | * ]: any one of numerous named for ]. | ||
| * ] |
* ]: any ] of a ] is an ]. | ||
| * ] on the ] of a set of forms. | * ] on the ] of a set of forms. | ||
| * ] regarding the line bundle <math>K_{M} \otimes L^{\otimes m}</math> constructed from a ] ] <math>L</math> on a ] ] <math>M</math> and the ] <math>K_{M}</math> of <math>M</math> | * ] regarding the line bundle <math>K_{M} \otimes L^{\otimes m}</math> constructed from a ] ] <math>L</math> on a ] ] <math>M</math> and the ] <math>K_{M}</math> of <math>M</math> | ||
| * Hartshorne's conjectures<ref>{{cite journal|title=On two conjectures of Hartshorne's |last1=Barlet |first1=Daniel |last2=Peternell |first2=Thomas |last3=Schneider |first3=Michael |doi=10.1007/BF01453563 |journal=] |year=1990 |volume=286 |issue=1–3 |pages=13–25|s2cid=122151259 }}</ref> | * Hartshorne's conjectures<ref>{{cite journal|title=On two conjectures of Hartshorne's |last1=Barlet |first1=Daniel |last2=Peternell |first2=Thomas |last3=Schneider |first3=Michael |doi=10.1007/BF01453563 |journal=] |year=1990 |volume=286 |issue=1–3 |pages=13–25|s2cid=122151259 }}</ref> | ||
| * ] |
* ]: if a ] over a ]-0 field has a constant nonzero ], then it has a ] (i.e. with polynomial components) inverse function. | ||
| * ] on the distribution of ]s of bounded ] in certain subsets of ] | * ] on the distribution of ]s of bounded ] in certain subsets of ] | ||
| * ] on an equivalence between ] and ]<ref>{{citation | * ] on an equivalence between ] and ]<ref>{{citation | ||
| Line 278: | Line 267: | ||
| |date=2004-06-05|bibcode=2003math.....12059M | |date=2004-06-05|bibcode=2003math.....12059M | ||
| }}</ref> | }}</ref> | ||
| * ] |
* ]: if a ] has a ring of ]s generated by its contained ], then it must be ]. | ||
| * ] |
* ]: the higher ] of any ] ] defined over a ] must vanish up to torsion. | ||
| * ] on splittings of ]s from ]s of complete ] over finitely-generated ] <math>k</math> to the ] of <math>k</math>. | * ] on splittings of ]s from ]s of complete ] over finitely-generated ] <math>k</math> to the ] of <math>k</math>. | ||
| * ] on algebraic cycles | * ] on algebraic cycles | ||
| * ] on the connection between ]s on ] and ] on ]. | * ] on the connection between ]s on ] and ] on ]. | ||
| * ] |
* ]: a certain ] encoding the ]s of a ] ] is fixed by an action of half of the ]. | ||
| * Zariski multiplicity conjecture on the topological equisingularity and equimultiplicity of ] at ]<ref>{{cite journal|last=Zariski |first=Oscar |author-link=Oscar Zariski |title=Some open questions in the theory of singularities |journal=] |volume=77 |issue=4 |year=1971 |pages=481–491 |doi=10.1090/S0002-9904-1971-12729-5 |mr=0277533|doi-access=free }}</ref> | * Zariski multiplicity conjecture on the topological equisingularity and equimultiplicity of ] at ]<ref>{{cite journal|last=Zariski |first=Oscar |author-link=Oscar Zariski |title=Some open questions in the theory of singularities |journal=] |volume=77 |issue=4 |year=1971 |pages=481–491 |doi=10.1090/S0002-9904-1971-12729-5 |mr=0277533|doi-access=free }}</ref> | ||
| =====Other===== | |||
| * Are infinite sequences of ] possible in dimensions greater than 3? | * Are infinite sequences of ] possible in dimensions greater than 3? | ||
| * ] in characteristic <math>p</math> | * ] in characteristic <math>p</math> | ||
| ====Covering and packing==== | ====Covering and packing==== | ||
| =====Conjectures and problems===== | |||
| * ] on upper and lower bounds for the number of smaller-diameter subsets needed to cover a ] ''n''-dimensional set. | * ] on upper and lower bounds for the number of smaller-diameter subsets needed to cover a ] ''n''-dimensional set. | ||
| * The ]: if the union of finitely many axis-parallel squares has unit area, how small can the largest area covered by a disjoint subset of squares be?<ref>{{citation|last1=Bereg|first1=Sergey|last2=Dumitrescu|first2=Adrian|last3=Jiang|first3=Minghui|doi=10.1007/s00453-009-9298-z|issue=3|journal=Algorithmica|mr=2609053|pages=538–561|title=On covering problems of Rado|volume=57|year=2010|s2cid=6511998}}</ref> | * The ]: if the union of finitely many axis-parallel squares has unit area, how small can the largest area covered by a disjoint subset of squares be?<ref>{{citation|last1=Bereg|first1=Sergey|last2=Dumitrescu|first2=Adrian|last3=Jiang|first3=Minghui|doi=10.1007/s00453-009-9298-z|issue=3|journal=Algorithmica|mr=2609053|pages=538–561|title=On covering problems of Rado|volume=57|year=2010|s2cid=6511998}}</ref> | ||
| * The ] |
* The ]: when <math>n</math> is a ], packing <math>n-1</math> circles in an equilateral triangle requires a triangle of the same size as packing <math>n</math> circles<ref>{{citation|last=Melissen|first=Hans|doi=10.2307/2324212|issue=10|journal=American Mathematical Monthly|mr=1252928|pages=916–925|title=Densest packings of congruent circles in an equilateral triangle|volume=100|year=1993|jstor=2324212}}</ref> | ||
| * The ] for dimensions other than 1, 2, 3, 4, 8 and 24<ref>{{citation |first=John H. |last=Conway |author-link=John Horton Conway |author2=Neil J.A. Sloane |author-link2=Neil Sloane |year=1999 |title=Sphere Packings, Lattices and Groups |edition=3rd |publisher=Springer-Verlag |location=New York |isbn=978-0-387-98585-5|pages=}}</ref> | * The ] for dimensions other than 1, 2, 3, 4, 8 and 24<ref>{{citation |first=John H. |last=Conway |author-link=John Horton Conway |author2=Neil J.A. Sloane |author-link2=Neil Sloane |year=1999 |title=Sphere Packings, Lattices and Groups |edition=3rd |publisher=Springer-Verlag |location=New York |isbn=978-0-387-98585-5|pages=}}</ref> | ||
| * ] |
* ]: the smoothed octagon has the lowest maximum packing density of all centrally-symmetric convex plane sets<ref>{{citation | ||
| | last = Hales | first = Thomas | author-link = Thomas Callister Hales | | last = Hales | first = Thomas | author-link = Thomas Callister Hales | ||
| | arxiv = 1703.01352 | | arxiv = 1703.01352 | ||
| Line 307: | Line 294: | ||
| ==== Differential geometry ==== | ==== Differential geometry ==== | ||
| {{Main|Differential geometry}} | {{Main|Differential geometry}} | ||
| * The ], a generalization of ] | |||
| =====Conjectures and problems===== | |||
| * ]: any convex, closed, and twice-differentiable surface in three-dimensional ] admits at least two ]s | |||
| * The ], a possible generalization of the original ] | |||
| * ] that any convex, closed, and twice-differentiable surface in three-dimensional ] admits at least two ]s | |||
| * ]: Can the classical ] for subsets of Euclidean space be extended to spaces of nonpositive curvature, known as ]? | * ]: Can the classical ] for subsets of Euclidean space be extended to spaces of nonpositive curvature, known as ]? | ||
| * ] that the ] of a ] ] vanishes. | * ] that the ] of a ] ] vanishes. | ||
| Line 349: | Line 335: | ||
| | volume = 31 | | volume = 31 | ||
| | year = 1997}}</ref> | | year = 1997}}</ref> | ||
| * ] |
* ]: a ] ] ] has an infinite number of ] closed ] ]s. | ||
| * ] that the first ] for the ] on an embedded ] of <math>S^{n+1}</math> is <math>n</math>. | * ] that the first ] for the ] on an embedded ] of <math>S^{n+1}</math> is <math>n</math>. | ||
| Line 355: | Line 341: | ||
| {{Main|Discrete geometry }} | {{Main|Discrete geometry }} | ||
| ] is 12, because 12 non-overlapping unit spheres can be put into contact with a central unit sphere. (Here, the centers of outer spheres form the vertices of a ].) Kissing numbers are only known exactly in dimensions 1, 2, 3, 4, 8 and 24.]] | ] is 12, because 12 non-overlapping unit spheres can be put into contact with a central unit sphere. (Here, the centers of outer spheres form the vertices of a ].) Kissing numbers are only known exactly in dimensions 1, 2, 3, 4, 8 and 24.]] | ||
| =====Conjectures and problems===== | |||
| * The ] on covering ''n''-dimensional convex bodies with at most 2<sup>''n''</sup> smaller copies<ref>{{citation|title=Results and Problems in Combinatorial Geometry|first1=V.|last1=Boltjansky|first2=I.|last2=Gohberg|publisher=Cambridge University Press|year=1985|contribution=11. Hadwiger's Conjecture|pages=44–46}}.</ref> | * The ] on covering ''n''-dimensional convex bodies with at most 2<sup>''n''</sup> smaller copies<ref>{{citation|title=Results and Problems in Combinatorial Geometry|first1=V.|last1=Boltjansky|first2=I.|last2=Gohberg|publisher=Cambridge University Press|year=1985|contribution=11. Hadwiger's Conjecture|pages=44–46}}.</ref> | ||
| * Solving the ] for arbitrary <math>n</math><ref>{{citation | * Solving the ] for arbitrary <math>n</math><ref>{{citation | ||
| Line 391: | Line 376: | ||
| | year = 1989| s2cid = 8917264 }}.</ref> | | year = 1989| s2cid = 8917264 }}.</ref> | ||
| * The ] on triangles in line arrangements<ref>{{MathWorld|urlname=KobonTriangle|title=Kobon Triangle}}</ref> | * The ] on triangles in line arrangements<ref>{{MathWorld|urlname=KobonTriangle|title=Kobon Triangle}}</ref> | ||
| * The ] |
* The ]: at most <math>2d</math> points can be equidistant in <math>L^1</math> spaces<ref>{{citation | ||
| | last = Guy | first = Richard K. | authorlink = Richard K. Guy | | last = Guy | first = Richard K. | authorlink = Richard K. Guy | ||
| | issue = 3 | | issue = 3 | ||
| Line 415: | Line 400: | ||
| *] on finding ]s for various planar shapes | *] on finding ]s for various planar shapes | ||
| =====Open questions===== | |||
| * ] can be determined by a set of {{mvar|n}} points in the Euclidean plane?<ref>{{citation | * ] can be determined by a set of {{mvar|n}} points in the Euclidean plane?<ref>{{citation | ||
| | last1 = Brass | first1 = Peter | | last1 = Brass | first1 = Peter | ||
| Line 428: | Line 412: | ||
| | year = 2005}}</ref> | | year = 2005}}</ref> | ||
| =====Other===== | |||
| * Finding matching upper and lower bounds for ] and halving lines<ref>{{citation | * Finding matching upper and lower bounds for ] and halving lines<ref>{{citation | ||
| | last = Dey | first = Tamal K. | author-link = Tamal Dey | | last = Dey | first = Tamal K. | author-link = Tamal Dey | ||
| Line 454: | Line 437: | ||
| ====Euclidean geometry==== | ====Euclidean geometry==== | ||
| {{Main|Euclidean geometry}} | {{Main|Euclidean geometry}} | ||
| =====Conjectures and problems===== | |||
| * The ] on the invertibility of a certain <math>n</math>-by-<math>n</math> matrix depending on <math>n</math> points in <math>\mathbb{R}^{3}</math><ref>{{Citation | last1=Atiyah | first1=Michael | author1-link=Michael Atiyah | title=Configurations of points | doi=10.1098/rsta.2001.0840 | mr=1853626 | year=2001 | journal= Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences| issn=1364-503X | volume=359 | issue=1784 | pages=1375–1387| bibcode=2001RSPTA.359.1375A | s2cid=55833332 }}</ref> | * The ] on the invertibility of a certain <math>n</math>-by-<math>n</math> matrix depending on <math>n</math> points in <math>\mathbb{R}^{3}</math><ref>{{Citation | last1=Atiyah | first1=Michael | author1-link=Michael Atiyah | title=Configurations of points | doi=10.1098/rsta.2001.0840 | mr=1853626 | year=2001 | journal= Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences| issn=1364-503X | volume=359 | issue=1784 | pages=1375–1387| bibcode=2001RSPTA.359.1375A | s2cid=55833332 }}</ref> | ||
| * ] – find the shortest route that is guaranteed to reach the boundary of a given shape, starting at an unknown point of the shape with unknown orientation<ref>{{citation|last1=Finch|first1=S. R.|last2=Wetzel|first2=J. E.|title=Lost in a forest|volume=11|issue=8|year=2004|journal=]|pages=645–654|mr=2091541|doi=10.2307/4145038|jstor=4145038}}</ref> | * ] – find the shortest route that is guaranteed to reach the boundary of a given shape, starting at an unknown point of the shape with unknown orientation<ref>{{citation|last1=Finch|first1=S. R.|last2=Wetzel|first2=J. E.|title=Lost in a forest|volume=11|issue=8|year=2004|journal=]|pages=645–654|mr=2091541|doi=10.2307/4145038|jstor=4145038}}</ref> | ||
| * Danzer's problem and Conway's dead fly problem – do ]s of bounded density or bounded separation exist?<ref>{{citation|last1=Solomon|first1=Yaar|last2=Weiss|first2=Barak|arxiv=1406.3807|doi=10.24033/asens.2303|issue=5|journal=Annales Scientifiques de l'École Normale Supérieure|mr=3581810|pages=1053–1074|title=Dense forests and Danzer sets|volume=49|year=2016|s2cid=672315}}; {{citation|last=Conway|first=John H.|author-link=John Horton Conway|access-date=2019-02-12|publisher=]|title=Five $1,000 Problems (Update 2017)|url=https://oeis.org/A248380/a248380.pdf|archive-url=https://web.archive.org/web/20190213123825/https://oeis.org/A248380/a248380.pdf|archive-date=2019-02-13|url-status=live}}</ref> | * Danzer's problem and Conway's dead fly problem – do ]s of bounded density or bounded separation exist?<ref>{{citation|last1=Solomon|first1=Yaar|last2=Weiss|first2=Barak|arxiv=1406.3807|doi=10.24033/asens.2303|issue=5|journal=Annales Scientifiques de l'École Normale Supérieure|mr=3581810|pages=1053–1074|title=Dense forests and Danzer sets|volume=49|year=2016|s2cid=672315}}; {{citation|last=Conway|first=John H.|author-link=John Horton Conway|access-date=2019-02-12|publisher=]|title=Five $1,000 Problems (Update 2017)|url=https://oeis.org/A248380/a248380.pdf|archive-url=https://web.archive.org/web/20190213123825/https://oeis.org/A248380/a248380.pdf|archive-date=2019-02-13|url-status=live}}</ref> | ||
| * ] |
* ]: a convex body <math>K</math> in <math>n</math> dimensions containing a single lattice point in its interior as its ] cannot have volume greater than <math>(n+1)^{n}/n!</math> | ||
| * The {{not a typo|]}} – does there exist a two-dimensional shape that forms the ] for an ], but not for any periodic tiling?<ref>{{citation|last1=Socolar|first1=Joshua E. S.|last2=Taylor|first2=Joan M.|arxiv=1009.1419|doi=10.1007/s00283-011-9255-y|issue=1|journal=The Mathematical Intelligencer|mr=2902144|pages=18–28|title=Forcing nonperiodicity with a single tile|volume=34|year=2012|s2cid=10747746}}</ref> | * The {{not a typo|]}} – does there exist a two-dimensional shape that forms the ] for an ], but not for any periodic tiling?<ref>{{citation|last1=Socolar|first1=Joshua E. S.|last2=Taylor|first2=Joan M.|arxiv=1009.1419|doi=10.1007/s00283-011-9255-y|issue=1|journal=The Mathematical Intelligencer|mr=2902144|pages=18–28|title=Forcing nonperiodicity with a single tile|volume=34|year=2012|s2cid=10747746}}</ref> | ||
| * ] |
* ]: sets of Hausdorff dimension greater than <math>d/2</math> in <math>\mathbb{R}^d</math> must have a distance set of nonzero ]<ref>{{citation|last1=Arutyunyants|first1=G.|last2=Iosevich|first2=A.|editor-last=Pach|editor-first=János|editor-link=János Pach|contribution=Falconer conjecture, spherical averages and discrete analogs|doi=10.1090/conm/342/06127|mr=2065249|pages=15–24|publisher=Amer. Math. Soc., Providence, RI|series=Contemp. Math.|title=Towards a Theory of Geometric Graphs|volume=342|year=2004|isbn=9780821834848|doi-access=free}}</ref> | ||
| * ], also known as ] and the square peg problem – does every ] have an inscribed square?<ref name="matschke">{{citation|last=Matschke|first=Benjamin|date=2014|title=A survey on the square peg problem|journal=]|volume=61|issue=4|pages=346–352|doi=10.1090/noti1100|doi-access=free}}</ref> | * ], also known as ] and the square peg problem – does every ] have an inscribed square?<ref name="matschke">{{citation|last=Matschke|first=Benjamin|date=2014|title=A survey on the square peg problem|journal=]|volume=61|issue=4|pages=346–352|doi=10.1090/noti1100|doi-access=free}}</ref> | ||
| * The ] – do <math>n</math>-dimensional sets that contain a unit line segment in every direction necessarily have ] and ] equal to <math>n</math>?<ref>{{citation|last1=Katz|first1=Nets|author1-link=Nets Katz|last2=Tao|first2=Terence|author2-link=Terence Tao|department=Proceedings of the 6th International Conference on Harmonic Analysis and Partial Differential Equations (El Escorial, 2000)|doi=10.5565/PUBLMAT_Esco02_07|issue=Vol. Extra|journal=Publicacions Matemàtiques|mr=1964819|pages=161–179|title=Recent progress on the Kakeya conjecture|year=2002|citeseerx=10.1.1.241.5335|s2cid=77088}}</ref> | * The ] – do <math>n</math>-dimensional sets that contain a unit line segment in every direction necessarily have ] and ] equal to <math>n</math>?<ref>{{citation|last1=Katz|first1=Nets|author1-link=Nets Katz|last2=Tao|first2=Terence|author2-link=Terence Tao|department=Proceedings of the 6th International Conference on Harmonic Analysis and Partial Differential Equations (El Escorial, 2000)|doi=10.5565/PUBLMAT_Esco02_07|issue=Vol. Extra|journal=Publicacions Matemàtiques|mr=1964819|pages=161–179|title=Recent progress on the Kakeya conjecture|year=2002|citeseerx=10.1.1.241.5335|s2cid=77088}}</ref> | ||
| Line 473: | Line 455: | ||
| * The ] – what is the minimum energy configuration of <math>n</math> mutually-repelling particles on a unit sphere?<ref>{{citation|last=Whyte|first=L. L.|doi=10.2307/2306764|journal=The American Mathematical Monthly|mr=0050303|pages=606–611|title=Unique arrangements of points on a sphere|volume=59|issue=9|year=1952|jstor=2306764}}</ref> | * The ] – what is the minimum energy configuration of <math>n</math> mutually-repelling particles on a unit sphere?<ref>{{citation|last=Whyte|first=L. L.|doi=10.2307/2306764|journal=The American Mathematical Monthly|mr=0050303|pages=606–611|title=Unique arrangements of points on a sphere|volume=59|issue=9|year=1952|jstor=2306764}}</ref> | ||
| =====Open questions===== | |||
| * ] — are there three unknotted space curves, not all three circles, which cannot be arranged to form this link?<ref>{{citation | * ] — are there three unknotted space curves, not all three circles, which cannot be arranged to form this link?<ref>{{citation | ||
| | last = Howards | first = Hugh Nelson | | last = Howards | first = Hugh Nelson | ||
| Line 488: | Line 469: | ||
| * ] – is it possible for ] of every dimension?<ref>{{citation|last1=Brandts|first1=Jan|last2=Korotov|first2=Sergey|last3=Křížek|first3=Michal|last4=Šolc|first4=Jakub|doi=10.1137/060669073|issue=2|journal=SIAM Review|mr=2505583|pages=317–335|title=On nonobtuse simplicial partitions|volume=51|year=2009|url=https://pure.uva.nl/ws/files/836396/73198_315330.pdf|bibcode=2009SIAMR..51..317B|access-date=2018-11-22|archive-url=https://web.archive.org/web/20181104211116/https://pure.uva.nl/ws/files/836396/73198_315330.pdf|archive-date=2018-11-04|url-status=live}}. See in particular Conjecture 23, p. 327.</ref> | * ] – is it possible for ] of every dimension?<ref>{{citation|last1=Brandts|first1=Jan|last2=Korotov|first2=Sergey|last3=Křížek|first3=Michal|last4=Šolc|first4=Jakub|doi=10.1137/060669073|issue=2|journal=SIAM Review|mr=2505583|pages=317–335|title=On nonobtuse simplicial partitions|volume=51|year=2009|url=https://pure.uva.nl/ws/files/836396/73198_315330.pdf|bibcode=2009SIAMR..51..317B|access-date=2018-11-22|archive-url=https://web.archive.org/web/20181104211116/https://pure.uva.nl/ws/files/836396/73198_315330.pdf|archive-date=2018-11-04|url-status=live}}. See in particular Conjecture 23, p. 327.</ref> | ||
| =====Other===== | |||
| * ]s – find and classify the complete set of these shapes<ref>{{citation|url=http://www.openproblemgarden.org/op/convex_uniform_5_polytopes|work=Open Problem Garden|title=Convex uniform 5-polytopes|access-date=2016-10-04|date=May 24, 2012|author=ACW|archive-url=https://web.archive.org/web/20161005164840/http://www.openproblemgarden.org/op/convex_uniform_5_polytopes|archive-date=October 5, 2016|url-status=live}}.</ref> | * ]s – find and classify the complete set of these shapes<ref>{{citation|url=http://www.openproblemgarden.org/op/convex_uniform_5_polytopes|work=Open Problem Garden|title=Convex uniform 5-polytopes|access-date=2016-10-04|date=May 24, 2012|author=ACW|archive-url=https://web.archive.org/web/20161005164840/http://www.openproblemgarden.org/op/convex_uniform_5_polytopes|archive-date=October 5, 2016|url-status=live}}.</ref> | ||
| Line 496: | Line 476: | ||
| ==== Graph coloring and labeling ==== | ==== Graph coloring and labeling ==== | ||
| ] | ] | ||
| =====Conjectures and problems===== | |||
| * ] on the diameter of the space of colorings of degenerate graphs<ref>{{citation | * ] on the diameter of the space of colorings of degenerate graphs<ref>{{citation | ||
| | last1 = Bousquet | first1 = Nicolas | | last1 = Bousquet | first1 = Nicolas | ||
| Line 547: | Line 526: | ||
| | publisher = Springer-Verlag | | publisher = Springer-Verlag | ||
| | year = 1991}}, Problem G10.</ref> | | year = 1991}}, Problem G10.</ref> | ||
| * ] |
* ]: every bridgeless cubic graph has a cycle-continuous mapping to the Petersen graph<ref>{{citation | ||
| | last1 = Hägglund | | last1 = Hägglund | ||
| | first1 = Jonas | | first1 = Jonas | ||
| Line 567: | Line 546: | ||
| | doi-access = free | | doi-access = free | ||
| }}.</ref> | }}.</ref> | ||
| * The ] |
* The ]:, for every graph, the list chromatic index equals the chromatic index<ref>{{citation|last1=Jensen|first1=Tommy R.|last2=Toft|first2=Bjarne|year=1995|title=Graph Coloring Problems|location=New York|publisher=Wiley-Interscience|isbn=978-0-471-02865-9|chapter=12.20 List-Edge-Chromatic Numbers|pages=201–202}}.</ref> | ||
| * The ] of Behzad and Vizing that the total chromatic number is at most two plus the maximum degree<ref>{{citation | * The ] of Behzad and Vizing that the total chromatic number is at most two plus the maximum degree<ref>{{citation | ||
| | last1 = Molloy | first1 = Michael | | last1 = Molloy | first1 = Michael | ||
| Line 583: | Line 562: | ||
| ==== Graph drawing ==== | ==== Graph drawing ==== | ||
| * The ]: the crossing number can be lower-bounded by the crossing number of a ] with the same ]<ref>{{citation|first1=János|last1=Barát|first2=Géza|last2=Tóth|year=2010|title=Towards the Albertson Conjecture|arxiv=0909.0413|journal=Electronic Journal of Combinatorics|volume=17|issue=1|page=R73|bibcode=2009arXiv0909.0413B|doi-access=free|doi=10.37236/345}}.</ref> | |||
| =====Conjectures and problems===== | |||
| * The ] that the crossing number can be lower-bounded by the crossing number of a ] with the same ]<ref>{{citation|first1=János|last1=Barát|first2=Géza|last2=Tóth|year=2010|title=Towards the Albertson Conjecture|arxiv=0909.0413|journal=Electronic Journal of Combinatorics|volume=17|issue=1|page=R73|bibcode=2009arXiv0909.0413B|doi-access=free|doi=10.37236/345}}.</ref> | |||
| * ]<ref>{{citation |last1=Fulek |first1=Radoslav |last2=Pach |first2=János |authorlink2=János Pach |title=A computational approach to Conway's thrackle conjecture|journal=] |volume=44 |year=2011|issue=6–7 |pages=345–355 |mr=2785903 |doi=10.1016/j.comgeo.2011.02.001|doi-access=free|arxiv=1002.3904 }}.</ref> that ]s cannot have more edges than vertices | * ]<ref>{{citation |last1=Fulek |first1=Radoslav |last2=Pach |first2=János |authorlink2=János Pach |title=A computational approach to Conway's thrackle conjecture|journal=] |volume=44 |year=2011|issue=6–7 |pages=345–355 |mr=2785903 |doi=10.1016/j.comgeo.2011.02.001|doi-access=free|arxiv=1002.3904 }}.</ref> that ]s cannot have more edges than vertices | ||
| * ] |
* ]: every planar graph can be drawn with integer edge lengths<ref>{{citation|title=Pearls in Graph Theory: A Comprehensive Introduction|title-link= Pearls in Graph Theory |series=Dover Books on Mathematics|last1=Hartsfield|first1=Nora|last2=Ringel|first2=Gerhard|author2-link=Gerhard Ringel|publisher=Courier Dover Publications|year=2013|isbn=978-0-486-31552-2|at=|mr=2047103}}.</ref> | ||
| * ] on projective-plane embeddings of graphs with planar covers<ref>{{citation | last = Hliněný | first = Petr | doi = 10.1007/s00373-010-0934-9 | issue = 4 | journal = ] | mr = 2669457 | pages = 525–536 | title = 20 years of Negami's planar cover conjecture | url = http://www.fi.muni.cz/~hlineny/papers/plcover20-gc.pdf | volume = 26 | year = 2010 | citeseerx = 10.1.1.605.4932 | s2cid = 121645 | access-date = 2016-10-04 | archive-url = https://web.archive.org/web/20160304030722/http://www.fi.muni.cz/~hlineny/papers/plcover20-gc.pdf | archive-date = 2016-03-04 | url-status = live }}.</ref> | * ] on projective-plane embeddings of graphs with planar covers<ref>{{citation | last = Hliněný | first = Petr | doi = 10.1007/s00373-010-0934-9 | issue = 4 | journal = ] | mr = 2669457 | pages = 525–536 | title = 20 years of Negami's planar cover conjecture | url = http://www.fi.muni.cz/~hlineny/papers/plcover20-gc.pdf | volume = 26 | year = 2010 | citeseerx = 10.1.1.605.4932 | s2cid = 121645 | access-date = 2016-10-04 | archive-url = https://web.archive.org/web/20160304030722/http://www.fi.muni.cz/~hlineny/papers/plcover20-gc.pdf | archive-date = 2016-03-04 | url-status = live }}.</ref> | ||
| * The ] |
* The ]: every polyhedral graph has a convex greedy embedding<ref>{{citation | last1 = Nöllenburg | first1 = Martin | last2 = Prutkin | first2 = Roman | last3 = Rutter | first3 = Ignaz | doi = 10.20382/jocg.v7i1a3 | issue = 1 | journal = ] | mr = 3463906 | pages = 47–69 | title = On self-approaching and increasing-chord drawings of 3-connected planar graphs | volume = 7 | year = 2016| arxiv = 1409.0315 | s2cid = 1500695 }}</ref> | ||
| * ] – Is there a drawing of any complete bipartite graph with fewer crossings than the number given by Zarankiewicz?<ref>{{citation | last1 = Pach | first1 = János | author1-link = János Pach | last2 = Sharir | first2 = Micha | author2-link = Micha Sharir | contribution = 5.1 Crossings—the Brick Factory Problem | pages = 126–127 | publisher = ] | series = Mathematical Surveys and Monographs | title = Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures | volume = 152 | year = 2009}}.</ref> | * ] – Is there a drawing of any complete bipartite graph with fewer crossings than the number given by Zarankiewicz?<ref>{{citation | last1 = Pach | first1 = János | author1-link = János Pach | last2 = Sharir | first2 = Micha | author2-link = Micha Sharir | contribution = 5.1 Crossings—the Brick Factory Problem | pages = 126–127 | publisher = ] | series = Mathematical Surveys and Monographs | title = Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures | volume = 152 | year = 2009}}.</ref> | ||
| =====Other===== | |||
| * ]s of subquadratic size for planar graphs<ref>{{citation | last1 = Demaine | first1 = E. | author1-link = Erik Demaine | last2 = O'Rourke | first2 = J. | author2-link = Joseph O'Rourke (professor) | contribution = Problem 45: Smallest Universal Set of Points for Planar Graphs | title = The Open Problems Project | url = http://cs.smith.edu/~orourke/TOPP/P45.html | year = 2002–2012 | access-date = 2013-03-19 | archive-url = https://web.archive.org/web/20120814154255/http://cs.smith.edu/~orourke/TOPP/P45.html | archive-date = 2012-08-14 | url-status = live }}.</ref> | * ]s of subquadratic size for planar graphs<ref>{{citation | last1 = Demaine | first1 = E. | author1-link = Erik Demaine | last2 = O'Rourke | first2 = J. | author2-link = Joseph O'Rourke (professor) | contribution = Problem 45: Smallest Universal Set of Points for Planar Graphs | title = The Open Problems Project | url = http://cs.smith.edu/~orourke/TOPP/P45.html | year = 2002–2012 | access-date = 2013-03-19 | archive-url = https://web.archive.org/web/20120814154255/http://cs.smith.edu/~orourke/TOPP/P45.html | archive-date = 2012-08-14 | url-status = live }}.</ref> | ||
| ==== Paths and cycles in graphs ==== | ==== Paths and cycles in graphs ==== | ||
| * ]: every cubic bipartite three-connected planar graph has a Hamiltonian cycle<ref>{{citation | |||
| =====Conjectures and problems===== | |||
| * ] that every cubic bipartite three-connected planar graph has a Hamiltonian cycle<ref>{{citation | |||
| | last = Florek | first = Jan | | last = Florek | first = Jan | ||
| | doi = 10.1016/j.disc.2010.01.018 | | doi = 10.1016/j.disc.2010.01.018 | ||
| Line 619: | Line 595: | ||
| | year = 2014| s2cid = 1377980 | | year = 2014| s2cid = 1377980 | ||
| }}</ref> | }}</ref> | ||
| * The ] |
* The ]: every bridgeless graph has a family of cycles that includes each edge twice<ref>{{citation | ||
| | last = Jaeger | first = F. | | last = Jaeger | first = F. | ||
| | contribution = A survey of the cycle double cover conjecture | | contribution = A survey of the cycle double cover conjecture | ||
| Line 654: | Line 630: | ||
| | volume = 97 | | volume = 97 | ||
| | year = 1991}}</ref> | | year = 1991}}</ref> | ||
| * ] |
* ]: every ] on the <math>n</math>-dimensional doubly-] ] can be routed with edge-disjoint ]. | ||
| ==== Word-representation of graphs ==== | ==== Word-representation of graphs ==== | ||
| *Are there any graphs on ''n'' vertices whose ] requires more than floor(''n''/2) copies of each letter?<ref name="KL15">{{Cite book|url=https://link.springer.com/book/10.1007/978-3-319-25859-1|title=Words and Graphs|series=Monographs in Theoretical Computer Science. An EATCS Series |year=2015 |doi=10.1007/978-3-319-25859-1 |isbn=978-3-319-25857-7 |s2cid=7727433 |via=link.springer.com}}</ref><ref name="K17"> |
*Are there any graphs on ''n'' vertices whose ] requires more than floor(''n''/2) copies of each letter?<ref name="KL15">{{Cite book|url=https://link.springer.com/book/10.1007/978-3-319-25859-1|title=Words and Graphs|series=Monographs in Theoretical Computer Science. An EATCS Series |year=2015 |doi=10.1007/978-3-319-25859-1 |isbn=978-3-319-25857-7 |s2cid=7727433 |via=link.springer.com}}</ref><ref name="K17">{{Cite conference |last=Kitaev |first=Sergey |date=2017-05-16 |title=A Comprehensive Introduction to the Theory of Word-Representable Graphs |url=https://arxiv.org/abs/1705.05924v1 |conference=] |language=en |doi=10.1007/978-3-319-62809-7_2}}</ref><ref name="KP18">{{Cite journal|url=https://doi.org/10.1134/S1990478918020084|title=Word-Representable Graphs: a Survey|first1=S. V.|last1=Kitaev|first2=A. V.|last2=Pyatkin|date=April 1, 2018|journal=Journal of Applied and Industrial Mathematics|volume=12|issue=2|pages=278–296|via=Springer Link|doi=10.1134/S1990478918020084|s2cid=125814097 }}</ref><ref name="KP18-2">{{Cite journal |last=Kitaev |first=Sergey V. |last2=Pyatkin |first2=Artem V. |date=2018 |title=Графы, представимые в виде слов. Обзор результатов |trans-title=Word-representable graphs: A survey |url=http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=da&paperid=894&option_lang=rus |journal=Дискретн. анализ и исслед. опер. |language=ru |volume=25 |issue=2 |pages=19–53 |doi=10.17377/daio.2018.25.588}}</ref> | ||
| *Characterise (non-)] ]s<ref name="KL15"/><ref name="K17"/><ref name="KP18"/><ref name="KP18-2"/> | *Characterise (non-)] ]s<ref name="KL15"/><ref name="K17"/><ref name="KP18"/><ref name="KP18-2"/> | ||
| *Characterise ]s in terms of (induced) forbidden subgraphs.<ref name="KL15"/><ref name="K17"/><ref name="KP18"/><ref name="KP18-2"/> | *Characterise ]s in terms of (induced) forbidden subgraphs.<ref name="KL15"/><ref name="K17"/><ref name="KP18"/><ref name="KP18-2"/> | ||
| *Characterise ] near-triangulations containing the complete graph ''K''<sub>4</sub> (such a characterisation is known for ''K''<sub>4</sub>-free planar graphs<ref name="Glen2019">{{cite arXiv |eprint=1605.01688|author1=Marc Elliot Glen|title=Colourability and word-representability of near-triangulations|class=math.CO|year=2016}}</ref>) | *Characterise ] near-triangulations containing the complete graph ''K''<sub>4</sub> (such a characterisation is known for ''K''<sub>4</sub>-free planar graphs<ref name="Glen2019">{{cite arXiv |eprint=1605.01688|author1=Marc Elliot Glen|title=Colourability and word-representability of near-triangulations|class=math.CO|year=2016}}</ref>) | ||
| *Classify graphs with representation number 3, that is, graphs that can be ] using 3 copies of each letter, but cannot be represented using 2 copies of each letter<ref name="Kit2013-3-repr"> |
*Classify graphs with representation number 3, that is, graphs that can be ] using 3 copies of each letter, but cannot be represented using 2 copies of each letter<ref name="Kit2013-3-repr">{{Cite journal |last=Kitaev |first=Sergey |date=2014-03-06 |title=On graphs with representation number 3 |url=https://arxiv.org/abs/1403.1616v1 |language=en |doi=10.48550/arXiv.1403.1616}}</ref> | ||
| *Is it true that out of all ]s, ]s require longest word-representants?<ref name="GKP18">{{cite journal|url = https://www.sciencedirect.com/science/article/pii/S0166218X18301045 | doi=10.1016/j.dam.2018.03.013 | volume=244 | title=On the representation number of a crown graph | year=2018 | journal=Discrete Applied Mathematics | pages=89–93 | last1 = Glen | first1 = Marc | last2 = Kitaev | first2 = Sergey | last3 = Pyatkin | first3 = Artem| arxiv=1609.00674 | s2cid=46925617 }}</ref> | *Is it true that out of all ]s, ]s require longest word-representants?<ref name="GKP18">{{cite journal|url = https://www.sciencedirect.com/science/article/pii/S0166218X18301045 | doi=10.1016/j.dam.2018.03.013 | volume=244 | title=On the representation number of a crown graph | year=2018 | journal=Discrete Applied Mathematics | pages=89–93 | last1 = Glen | first1 = Marc | last2 = Kitaev | first2 = Sergey | last3 = Pyatkin | first3 = Artem| arxiv=1609.00674 | s2cid=46925617 }}</ref> | ||
| *Is the ] of a non-] graph always non-]?<ref name="KL15"/><ref name="K17"/><ref name="KP18"/><ref name="KP18-2"/> | *Is the ] of a non-] graph always non-]?<ref name="KL15"/><ref name="K17"/><ref name="KP18"/><ref name="KP18-2"/> | ||
| Line 667: | Line 643: | ||
| ==== Miscellaneous graph theory ==== | ==== Miscellaneous graph theory ==== | ||
| =====Conjectures and problems===== | |||
| * ]: which groups are Babai invariant groups? | * ]: which groups are Babai invariant groups? | ||
| * ] on upper bounds for sums of ] of ] of graphs in terms of their number of edges. | * ] on upper bounds for sums of ] of ] of graphs in terms of their number of edges. | ||
| Line 804: | Line 779: | ||
| * ]: how many edges can there be in a ] on a given number of vertices with no ] of a given size? | * ]: how many edges can there be in a ] on a given number of vertices with no ] of a given size? | ||
| =====Open questions===== | |||
| * Does a ] with girth 5 and degree 57 exist?<ref>{{citation|last=Ducey|first=Joshua E.|doi=10.1016/j.disc.2016.10.001|issue=5|journal=]|mr=3612450|pages=1104–1109|title=On the critical group of the missing Moore graph|volume=340|year=2017|arxiv=1509.00327|s2cid=28297244}}</ref> | * Does a ] with girth 5 and degree 57 exist?<ref>{{citation|last=Ducey|first=Joshua E.|doi=10.1016/j.disc.2016.10.001|issue=5|journal=]|mr=3612450|pages=1104–1109|title=On the critical group of the missing Moore graph|volume=340|year=2017|arxiv=1509.00327|s2cid=28297244}}</ref> | ||
| * What is the largest possible ] of an {{mvar|n}}-vertex ]?<ref>{{citation | * What is the largest possible ] of an {{mvar|n}}-vertex ]?<ref>{{citation | ||
| Line 821: | Line 795: | ||
| {{Main|Group theory }} | {{Main|Group theory }} | ||
| ] <math>B(2,3)</math> is finite; in its ], shown here, each of its 27 elements is represented by a vertex. The question of which other groups <math>B(m,n)</math> are finite remains open.]] | ] <math>B(2,3)</math> is finite; in its ], shown here, each of its 27 elements is represented by a vertex. The question of which other groups <math>B(m,n)</math> are finite remains open.]] | ||
| * ]: every balanced ] of the ] can be transformed into a trivial presentation by a sequence of ]s on ] and conjugations of relators | |||
| ====Notebook problems==== | |||
| * The Kourovka Notebook is a collection of unsolved problems in group theory, first published in 1965 and updated many times since.<ref>{{citation | |||
| | last1 = Khukhro | first1 = Evgeny I. | |||
| | last2 = Mazurov | first2 = Victor D. |author-link2 = Victor Mazurov | |||
| | arxiv = 1401.0300v16 | |||
| | title = Unsolved Problems in Group Theory. The Kourovka Notebook | |||
| | year = 2019}}</ref> | |||
| ====Conjectures and problems==== | |||
| * ] that every balanced ] of the ] can be transformed into a trivial presentation by a sequence of ]s on ] and conjugations of relators | |||
| * Guralnick–Thompson conjecture on the composition factors of groups in genus-0 systems<ref>{{citation |last=Aschbacher |first=Michael |author-link=Michael Aschbacher |title=On Conjectures of Guralnick and Thompson |journal=] |volume=135 |issue=2 |pages=277–343 |year=1990 |doi=10.1016/0021-8693(90)90292-V}}</ref> | * Guralnick–Thompson conjecture on the composition factors of groups in genus-0 systems<ref>{{citation |last=Aschbacher |first=Michael |author-link=Michael Aschbacher |title=On Conjectures of Guralnick and Thompson |journal=] |volume=135 |issue=2 |pages=277–343 |year=1990 |doi=10.1016/0021-8693(90)90292-V}}</ref> | ||
| * ] |
* ]: if a finite system of left ]s of subgroups of a group <math>G</math> form a partition of <math>G</math>, then the finite indices of said subgroups cannot be distinct. | ||
| * The ]: is every finite group the Galois group of a Galois extension of the rationals? | * The ]: is every finite group the Galois group of a Galois extension of the rationals? | ||
| * ] consider generalizations of groups | * ] consider generalizations of groups | ||
| ====Open questions==== | |||
| * Are there an infinite number of ]s? | * Are there an infinite number of ]s? | ||
| * Does ] exist? | * Does ] exist? | ||
| Line 843: | Line 807: | ||
| * Is every group ]? | * Is every group ]? | ||
| ==== Notebook problems ==== | |||
| * The Kourovka Notebook is a collection of unsolved problems in group theory, first published in 1965 and updated many times since.<ref>{{citation |last1=Khukhro |first1=Evgeny I. |title=Unsolved Problems in Group Theory. The Kourovka Notebook |year=2019 |arxiv=1401.0300v16 |last2=Mazurov |first2=Victor D. |author-link2=Victor Mazurov}}</ref> | |||
| === Model theory and formal languages === | === Model theory and formal languages === | ||
| {{Main|Model theory|formal languages}} |
{{Main|Model theory|formal languages}} | ||
| ====Conjectures and problems==== | |||
| * The ]: A simple group whose first-order theory is ] in <math>\aleph_0</math> is a simple algebraic group over an algebraically closed field. | * The ]: A simple group whose first-order theory is ] in <math>\aleph_0</math> is a simple algebraic group over an algebraically closed field. | ||
| * ]: can all ]s be expressed using ] with limited nesting depths of ]s? | * ]: can all ]s be expressed using ] with limited nesting depths of ]s? | ||
| Line 865: | Line 830: | ||
| * The universality problem for C-free graphs: For which finite sets C of graphs does the class of C-free countable graphs have a universal member under strong embeddings?<ref>{{cite journal |last1=Cherlin |first1=G. |last2=Shelah |first2=S. |date=May 2007 |title=Universal graphs with a forbidden subtree |journal=] |arxiv=math/0512218 |doi=10.1016/j.jctb.2006.05.008 |volume=97 |issue=3 |pages=293–333|s2cid=10425739 }}</ref> | * The universality problem for C-free graphs: For which finite sets C of graphs does the class of C-free countable graphs have a universal member under strong embeddings?<ref>{{cite journal |last1=Cherlin |first1=G. |last2=Shelah |first2=S. |date=May 2007 |title=Universal graphs with a forbidden subtree |journal=] |arxiv=math/0512218 |doi=10.1016/j.jctb.2006.05.008 |volume=97 |issue=3 |pages=293–333|s2cid=10425739 }}</ref> | ||
| * The universality spectrum problem: Is there a first-order theory whose universality spectrum is minimum?<ref>Džamonja, Mirna, "Club guessing and the universal models." ''On PCF'', ed. M. Foreman, (Banff, Alberta, 2004).</ref> | * The universality spectrum problem: Is there a first-order theory whose universality spectrum is minimum?<ref>Džamonja, Mirna, "Club guessing and the universal models." ''On PCF'', ed. M. Foreman, (Banff, Alberta, 2004).</ref> | ||
| * ] |
* ]: the number of ] models of a ] ] in a countable ] is either finite, <math>\aleph_{0}</math>, or <math>2^{\aleph_{0}}</math>. | ||
| ====Open questions==== | |||
| * Assume K is the class of models of a countable first order theory omitting countably many ]. If K has a model of cardinality <math>\aleph_{\omega_1}</math> does it have a model of cardinality continuum?<ref>{{cite journal |last=Shelah |first=Saharon |author-link=Saharon Shelah |date=1999 |title=Borel sets with large squares |journal=] |arxiv=math/9802134 |volume=159 |issue=1 |pages=1–50|bibcode=1998math......2134S |doi=10.4064/fm-159-1-1-50 |s2cid=8846429 }}</ref> | * Assume K is the class of models of a countable first order theory omitting countably many ]. If K has a model of cardinality <math>\aleph_{\omega_1}</math> does it have a model of cardinality continuum?<ref>{{cite journal |last=Shelah |first=Saharon |author-link=Saharon Shelah |date=1999 |title=Borel sets with large squares |journal=] |arxiv=math/9802134 |volume=159 |issue=1 |pages=1–50|bibcode=1998math......2134S |doi=10.4064/fm-159-1-1-50 |s2cid=8846429 }}</ref> | ||
| * Do the ]s have the ]? | * Do the ]s have the ]? | ||
| Line 878: | Line 842: | ||
| * Is there a logic L which satisfies both the Beth property and Δ-interpolation, is compact but does not satisfy the interpolation property?<ref>Makowsky J, "Compactness, embeddings and definability," in ''Model-Theoretic Logics'', eds Barwise and Feferman, Springer 1985 pps. 645–715.</ref> | * Is there a logic L which satisfies both the Beth property and Δ-interpolation, is compact but does not satisfy the interpolation property?<ref>Makowsky J, "Compactness, embeddings and definability," in ''Model-Theoretic Logics'', eds Barwise and Feferman, Springer 1985 pps. 645–715.</ref> | ||
| ====Other==== | |||
| * Determine the structure of Keisler's order<ref>{{cite journal | last1 = Keisler | first1 = HJ | year = 1967 | title = Ultraproducts which are not saturated | journal = J. Symb. Log. | volume = 32 | issue = 1| pages = 23–46 | doi=10.2307/2271240| jstor = 2271240 | s2cid = 250345806 }}</ref><ref>], ], "A dividing line in simple unstable theories." https://arxiv.org/abs/1208.2140 {{Webarchive|url=https://web.archive.org/web/20170802171447/https://arxiv.org/abs/1208.2140 |date=2017-08-02 }}</ref> | * Determine the structure of Keisler's order<ref>{{cite journal | last1 = Keisler | first1 = HJ | year = 1967 | title = Ultraproducts which are not saturated | journal = J. Symb. Log. | volume = 32 | issue = 1| pages = 23–46 | doi=10.2307/2271240| jstor = 2271240 | s2cid = 250345806 }}</ref><ref>], ], "A dividing line in simple unstable theories." https://arxiv.org/abs/1208.2140 {{Webarchive|url=https://web.archive.org/web/20170802171447/https://arxiv.org/abs/1208.2140 |date=2017-08-02 }}</ref> | ||
| Line 887: | Line 850: | ||
| ==== General ==== | ==== General ==== | ||
| ] because it is the sum of its proper positive divisors, 1, 2 and 3. It is not known how many perfect numbers there are, nor if any of them are odd.]] | ] because it is the sum of its proper positive divisors, 1, 2 and 3. It is not known how many perfect numbers there are, nor if any of them are odd.]] | ||
| * ]: a generalization of the ''abc'' conjecture to more than three integers. | |||
| ** ]: for any <math>\epsilon > 0</math>, <math>\text{rad}(abc)^{1+\epsilon} < c</math> is true for only finitely many positive <math>a, b, c</math> such that <math>a + b = c</math>. | |||
| =====Conjectures, problems and hypotheses===== | |||
| ** ]: for any <math>\epsilon > 0</math>, there is some constant <math>C(\epsilon)</math> such that, for any elliptic curve <math>E</math> defined over <math>\mathbb{Q}</math> with minimal discriminant <math>\Delta</math> and conductor <math>f</math>, we have <math>|\Delta| \leq C(\epsilon) \cdot f^{6+\epsilon}</math>. | |||
| * ]: a generalization of the abc conjecture to more than three integers. | |||
| ** ] that for any <math>\epsilon > 0</math>, <math>rad(abc)^{1+\epsilon} < c</math> is true for only finitely many positive <math>a, b, c</math> such that <math>a + b = c</math>. | |||
| ** ] that for any <math>\epsilon > 0</math>, there is some constant <math>C(\epsilon)</math> such that for any elliptic curve <math>E</math> defined over <math>\mathbb{Q}</math> with minimal discriminant <math>\Delta</math> and conductor <math>f</math>, we have <math>|\Delta| \leq C(\epsilon) \cdot f^{6+\epsilon}</math>. | |||
| *] | *] | ||
| * ]: classify ]s over ]s. | * ]: classify ]s over ]s. | ||
| * ]: find the most general ] for the ] of <math>k</math>-th order in a general ], where <math>k</math> is a power of a prime. | * ]: find the most general ] for the ] of <math>k</math>-th order in a general ], where <math>k</math> is a power of a prime. | ||
| * ]: extend the ] on ]s of <math>\mathbb{Q}</math> to any base number field. | * ]: extend the ] on ]s of <math>\mathbb{Q}</math> to any base number field. | ||
| *] |
*]: do the nontrivial zeros of all ]s lie on the critical line <math>1/2 + it</math> with real <math>t</math>? | ||
| **] |
**]: do the nontrivial zeros of all ]s lie on the critical line <math>1/2 + it</math> with real <math>t</math>? | ||
| ***] |
***]: do the nontrivial zeros of the ] lie on the critical line <math>1/2 + it</math> with real <math>t</math>? | ||
| *] |
*]: is every irreducible component of the ] of a set of special points in a ] a special ]? | ||
| *] | *] | ||
| * ]: are there any integer solutions to <math>n! + 1 = m^{2}</math> other than <math>n = 4, 5, 7</math>? | * ]: are there any integer solutions to <math>n! + 1 = m^{2}</math> other than <math>n = 4, 5, 7</math>? | ||
| * ] |
* ]: do all values of ] have ] greater than <math>1</math>? | ||
| * ] |
* ]: if a polynomial of degree <math>d</math> defined over a ] <math>K</math> of ] <math>0</math> has a factor in common with its first through <math>d - 1</math>-th derivative, then must <math>f</math> be the <math>d</math>-th power of a linear polynomial? | ||
| * ]: no ]s are infinite but non-repeating. | * ]: no ]s are infinite but non-repeating. | ||
| * ] (a corollary to ], per ]): determine precisely what rational numbers are ]s. | * ] (a corollary to ], per ]): determine precisely what rational numbers are ]s. | ||
| * Erdős–Moser problem: is <math>1^{1} + 2^{1} = 3^{1}</math> the only solution to the ]? | * Erdős–Moser problem: is <math>1^{1} + 2^{1} = 3^{1}</math> the only solution to the ]? | ||
| * ] |
* ]: for every <math>n \geq 2</math>, there are positive integers <math>x, y, z</math> such that <math>4/n = 1/x + 1/y + 1/z</math>. | ||
| * ]: is there a ] of points in the plane all at rational distances from one-another? | * ]: is there a ] of points in the plane all at rational distances from one-another? | ||
| * ]: for all <math>\epsilon > 0</math>, the pair <math>(\epsilon, 1/2 + \epsilon)</math> is an ]. | * ]: for all <math>\epsilon > 0</math>, the pair <math>(\epsilon, 1/2 + \epsilon)</math> is an ]. | ||
| * The ]: how far can the number of integer points in a circle centered at the origin be from the area of the circle? | * The ]: how far can the number of integer points in a circle centered at the origin be from the area of the circle? | ||
| * ] on solutions to <math>(x^{m} - 1)/(x - 1) = (y^{n} - 1)/(y - 1)</math> where <math>x > y > 1</math> and <math>m, n > 2</math>. | * ] on solutions to <math>(x^{m} - 1)/(x - 1) = (y^{n} - 1)/(y - 1)</math> where <math>x > y > 1</math> and <math>m, n > 2</math>. | ||
| * ] |
* ]: each element of a set of consecutive ]s can be assigned a distinct ] that divides it. | ||
| * ] |
* ]: for any <math>\epsilon > 0</math>, there is some constant <math>c(\epsilon)</math> such that either <math>y^{2} = x^{3}</math> or <math>|y^{2} - x^{3}| > c(\epsilon)x^{1/2 - \epsilon}</math>. | ||
| * ] |
* ]: the nontrivial zeros of the ] correspond to ] of a ]. | ||
| * Keating–Snaith conjecture concerning the asymptotics of an integral involving the ]<ref>{{citation | * Keating–Snaith conjecture concerning the asymptotics of an integral involving the ]<ref>{{citation | ||
| |last=Conrey |first=Brian |author-link=Brian Conrey | |last=Conrey |first=Brian |author-link=Brian Conrey | ||
| Line 922: | Line 883: | ||
| |volume=53 |number=3 |pages=507–512 |year=2016|doi-access=free}}</ref> | |volume=53 |number=3 |pages=507–512 |year=2016|doi-access=free}}</ref> | ||
| *]: if <math>\phi(n)</math> divides <math>n - 1</math>, must <math>n</math> be prime? | *]: if <math>\phi(n)</math> divides <math>n - 1</math>, must <math>n</math> be prime? | ||
| * ] |
* ]: a ] analogue of the ] of an ] does not vanish. | ||
| * ] that for all <math>\epsilon > 0</math>, <math>\zeta(1/2 + it) = o(t^{\epsilon})</math> | * ] that for all <math>\epsilon > 0</math>, <math>\zeta(1/2 + it) = o(t^{\epsilon})</math> | ||
| ** The ] for zeroes of the Riemann zeta function | ** The ] for zeroes of the Riemann zeta function | ||
| * ] |
* ]: for any two real numbers <math>\alpha, \beta</math>, <math>\liminf_{n \rightarrow \infty} n\,\Vert n\alpha\Vert\,\Vert n\beta\Vert = 0</math>, where <math>\Vert x\Vert</math> is the distance from <math>x</math> to the nearest integer. | ||
| * ] that no real number <math>x</math> has the property that the fractional parts of <math>x(3/2)^{n}</math> are less than <math>1/2</math> for all positive integers <math>n</math>. | * ] that no real number <math>x</math> has the property that the fractional parts of <math>x(3/2)^{n}</math> are less than <math>1/2</math> for all positive integers <math>n</math>. | ||
| * ] |
* ]: the normalized pair ] between pairs of zeros of the ] is the same as the pair correlation function of ]. | ||
| * ] |
* ]: the ] satisfies any arbitrary congruence infinitely often. | ||
| * ] |
* ]: for any <math>A, B, C</math>, the equation <math>Ax^{m} - By^{n} = C</math> has finitely many solutions when <math>m, n</math> are not both <math>2</math>. | ||
| * ] on bounding <math>\Delta_{k}(x) = D_{k}(x) - xP_{k}(log(x))</math> | * ] on bounding <math>\Delta_{k}(x) = D_{k}(x) - xP_{k}(log(x))</math> | ||
| ** ]: the specific case of the Piltz divisor problem for <math>k = 1</math> | ** ]: the specific case of the Piltz divisor problem for <math>k = 1</math> | ||
| * ]: a number of related conjectures that are generalizations of the original conjecture. | * ]: a number of related conjectures that are generalizations of the original conjecture. | ||
| * ]: also a number of related conjectures that are generalizations of the original conjecture. | * ]: also a number of related conjectures that are generalizations of the original conjecture. | ||
| * ] |
* ]: the length of the shortest ] producing <math>2^{n} - 1</math> is at most <math>n - 1</math> plus the length of the shortest addition chain producing <math>n</math>. | ||
| * Do ]s exist? | * Do ]s exist? | ||
| * ]: is there a finite upper bound on the multiplicities of the entries greater than 1 in ]?<ref>{{citation | * ]: is there a finite upper bound on the multiplicities of the entries greater than 1 in ]?<ref>{{citation | ||
| Line 958: | Line 919: | ||
| * ] on ] of points on ] over ]s. | * ] on ] of points on ] over ]s. | ||
| =====Open questions===== | |||
| * Are there infinitely many ]s? | * Are there infinitely many ]s? | ||
| *Do any ]s exist? | *Do any ]s exist? | ||
| Line 988: | Line 948: | ||
| | s2cid = 835158 | | s2cid = 835158 | ||
| }}</ref> | }}</ref> | ||
| * Is |
* Is <math>\pi</math> a ] (i.e., is each digit 0–9 equally frequent)?<ref>{{cite web|url=http://www2.lbl.gov/Science-Articles/Archive/pi-random.html|title=Are the Digits of Pi Random? Berkeley Lab Researcher May Hold Key|access-date=2016-03-18|archive-url=https://web.archive.org/web/20160327035021/http://www2.lbl.gov/Science-Articles/Archive/pi-random.html|archive-date=2016-03-27|url-status=live}}</ref> | ||
| * Is 10 a ]? | * Is 10 a ]? | ||
| * Can a 3×3 ] be constructed from 9 distinct perfect square numbers?{{ |
* Can a 3×3 ] be constructed from 9 distinct perfect square numbers?<ref>{{Cite journal |last=Robertson |first=John P. |date=1996-10-01 |title=Magic Squares of Squares |url=https://doi.org/10.1080/0025570X.1996.11996457 |journal=Mathematics Magazine |volume=69 |issue=4 |pages=289–293 |doi=10.1080/0025570X.1996.11996457 |issn=0025-570X}}</ref> | ||
| * Which integers can be written as the ]?<ref>{{Cite arXiv |eprint = 1604.07746|last1 = Huisman |first1 = Sander G.|title = Newer sums of three cubes|class = math.NT|year = 2016}}</ref> | * Which integers can be written as the ]?<ref>{{Cite arXiv |eprint = 1604.07746|last1 = Huisman |first1 = Sander G.|title = Newer sums of three cubes|class = math.NT|year = 2016}}</ref> | ||
| * ] | * ] | ||
| * Find the value of the ]. | |||
| =====Other===== | |||
| * Find the value of the ] | |||
| ==== Additive number theory ==== | ==== Additive number theory ==== | ||
| {{Main|Additive number theory }} | {{Main|Additive number theory }} | ||
| =====Conjectures and problems===== | |||
| {{See also|Problems involving arithmetic progressions}} | {{See also|Problems involving arithmetic progressions}} | ||
| * ] |
* ]: for all integral solutions to <math>A^{x} + B^{y} = C^{z}</math> where <math>x, y, z > 2</math>, all three numbers <math>A, B, C</math> must share some prime factor. | ||
| * ] that if the sum of the reciprocals of the members of a set of positive integers diverges, then the set contains arbitrarily long ]s. | * ] that if the sum of the reciprocals of the members of a set of positive integers diverges, then the set contains arbitrarily long ]s. | ||
| * ] that if <math>B</math> is an ] of order <math>2</math>, then the number of ways that positive integers <math>n</math> can be expressed as the sum of two numbers in <math>B</math> must tend to infinity as <math>n</math> tends to infinity. | * ] that if <math>B</math> is an ] of order <math>2</math>, then the number of ways that positive integers <math>n</math> can be expressed as the sum of two numbers in <math>B</math> must tend to infinity as <math>n</math> tends to infinity. | ||
| * ] |
* ]: there are finitely many distinct solutions <math>(a^{m}, b^{n}, c^{k})</math> to the equation <math>a^{m} + b^{n} = c^{k}</math> with <math>a, b, c</math> being positive ] and <math>m, n, k</math> being positive integers satisfying <math>1/m + 1/n + 1/k < 1</math>. | ||
| * ] on consecutive applications of the unsigned ] operator to the sequence of ]s. | * ] on consecutive applications of the unsigned ] operator to the sequence of ]s. | ||
| * ] |
* ]: every even natural number greater than <math>2</math> is the sum of two ]s. | ||
| * ] |
* ]: if the sum of <math>m</math> <math>k</math>-th powers of positive integers is equal to a different sum of <math>n</math> <math>k</math>-th powers of positive integers, then <math>m + n \geq k</math>. | ||
| * ] |
* ]: all odd integers greater than <math>5</math> can be represented as the sum of an odd ] and an even ]. | ||
| * ] of estimating the minimum possible maximum number of times a number appears in the termwise difference of two equally large sets partitioning the set <math>\{1, \ldots, 2n\}</math> | * ] of estimating the minimum possible maximum number of times a number appears in the termwise difference of two equally large sets partitioning the set <math>\{1, \ldots, 2n\}</math> | ||
| * ] | * ] | ||
| Line 1,014: | Line 972: | ||
| * The values of ''g''(''k'') and ''G''(''k'') in ] | * The values of ''g''(''k'') and ''G''(''k'') in ] | ||
| =====Open questions===== | |||
| * Do the ]s have a positive density? | * Do the ]s have a positive density? | ||
| =====Other===== | |||
| * Determine growth rate of ''r''<sub>''k''</sub>(''N'') (see ]) | * Determine growth rate of ''r''<sub>''k''</sub>(''N'') (see ]) | ||
| ==== Algebraic number theory ==== | ==== Algebraic number theory ==== | ||
| {{Main|Algebraic number theory }} | {{Main|Algebraic number theory }} | ||
| =====Conjectures and problems===== | |||
| * ]: are there infinitely many ] with ]? | * ]: are there infinitely many ] with ]? | ||
| * ]: actually numerous conjectures, all proposed by ] and ]. | * ]: actually numerous conjectures, all proposed by ] and ]. | ||
| Line 1,028: | Line 983: | ||
| * ] | * ] | ||
| * ]: is it possible, for any natural number <math>n</math>, to assign a sequence of ]s to each ] such that the sequence for <math>x</math> is eventually ] if and only if <math>x</math> is ] of degree <math>n</math>? | * ]: is it possible, for any natural number <math>n</math>, to assign a sequence of ]s to each ] such that the sequence for <math>x</math> is eventually ] if and only if <math>x</math> is ] of degree <math>n</math>? | ||
| * ] |
* ]: primes <math>p</math> do not divide the ] of the maximal real ] of the <math>p</math>-th ]. | ||
| * Lang and Trotter's conjecture on ] that the number of ] less than a constant <math>X</math> is within a constant multiple of <math>\sqrt{X}/\ln{X}</math> | * Lang and Trotter's conjecture on ] that the number of ] less than a constant <math>X</math> is within a constant multiple of <math>\sqrt{X}/\ln{X}</math> | ||
| * ] |
* ]: the ] of the ] on ]s of ]s are at least <math>1/4</math>. | ||
| * ] (including ]) | * ] (including ]) | ||
| =====Other===== | |||
| * Characterize all algebraic number fields that have some ]. | * Characterize all algebraic number fields that have some ]. | ||
| ====Computational number theory==== | ====Computational number theory==== | ||
| {{Main|Computational number theory}} | {{Main|Computational number theory}} | ||
| * ] |
* Can ] be done in ]? | ||
| ==== Prime numbers ==== | ==== Prime numbers ==== | ||
| Line 1,048: | Line 1,002: | ||
| * ] on the ]s that <math>p</math> is prime if and only if <math>pB_{p-1} \equiv -1 \pmod p</math> | * ] on the ]s that <math>p</math> is prime if and only if <math>pB_{p-1} \equiv -1 \pmod p</math> | ||
| * ] that if an integer is neither a perfect square nor <math>-1</math>, then it is a ] modulo infinitely many ]s <math>p</math> | * ] that if an integer is neither a perfect square nor <math>-1</math>, then it is a ] modulo infinitely many ]s <math>p</math> | ||
| * ] |
* ]: there are always at least <math>4</math> ]s between consecutive squares of prime numbers, aside from <math>2^{2}</math> and <math>3^{2}</math>. | ||
| * ] |
* ]: if an integer-coefficient polynomial <math>f</math> has a positive leading coefficient, is irreducible over the integers, and has no common factors over all <math>f(x)</math> where <math>x</math> is a positive integer, then <math>f(x)</math> is prime infinitely often. | ||
| * ] |
* ]: some ] is composite and thus all Catalan–Mersenne numbers are composite after some point. | ||
| * ] |
* ]: for a finite set of linear forms <math>a_{1} + b_{1}n, \ldots, a_{k} + b_{k}n</math> with each <math>b_{i} \geq 1</math>, there are infinitely many <math>n</math> for which all forms are ], unless there is some ] condition preventing it. | ||
| * ] |
* ]: every number greater than <math>2408</math> is the sum of two ] which both have ]. | ||
| * ] on the distribution of ]s in ]s. | * ] on the distribution of ]s in ]s. | ||
| * ] |
* ]: no three consecutive numbers are all ]. | ||
| * ] |
* ]: for all distinct ]s <math>p</math> and <math>q</math>, <math>(p^{q} - 1)/(p - 1)</math> does not divide <math>(q^{p} - 1)/(q - 1)</math> | ||
| * Fortune's conjecture that no ] is composite. | * Fortune's conjecture that no ] is composite. | ||
| * The ] problem: is it possible to find an infinite sequence of distinct ]s such that the difference between consecutive numbers in the sequence is bounded? | * The ] problem: is it possible to find an infinite sequence of distinct ]s such that the difference between consecutive numbers in the sequence is bounded? | ||
| * ] on the distribution of ] divisors of ]. | * ] on the distribution of ] divisors of ]. | ||
| * ] |
* ]: all even ]s greater than <math>2</math> are the sum of two ]s. | ||
| * ] | * ] | ||
| * Problems associated to ] | * Problems associated to ] | ||
| * ] |
* ]: for any odd ] <math>p</math>, if any two of the three conditions <math>p = 2^{k} \pm 1</math> or <math>p = 4^{k} \pm 3</math>, <math>2^{p} - 1</math> is prime, and <math>(2^{p} + 1)/3</math> is prime are true, then the third condition is true. | ||
| * ] |
* ]: for all positive even numbers <math>n</math>, there are infinitely many ]s of size <math>n</math>. | ||
| * ] that for every finite collection <math>\{f_{1}, \ldots, f_{k}\}</math> of nonconstant ]s over the integers with positive leading coefficients, either there are infinitely many positive integers <math>n</math> for which <math>f_{1}(n), \ldots, f_{k}(n)</math> are all ], or there is some fixed divisor <math>m > 1</math> which, for all <math>n</math>, divides some <math>f_{i}(n)</math>. | * ] that for every finite collection <math>\{f_{1}, \ldots, f_{k}\}</math> of nonconstant ]s over the integers with positive leading coefficients, either there are infinitely many positive integers <math>n</math> for which <math>f_{1}(n), \ldots, f_{k}(n)</math> are all ], or there is some fixed divisor <math>m > 1</math> which, for all <math>n</math>, divides some <math>f_{i}(n)</math>. | ||
| * ]: is 78,557 the lowest ]? | * ]: is 78,557 the lowest ]? | ||
| * ] |
* ]: there are infinitely many ]s. | ||
| * Does the ] hold for all natural numbers? | * Does the ] hold for all natural numbers? | ||
| =====Open questions===== | |||
| * Are all ]s ]? | * Are all ]s ]? | ||
| * Are all ]s ]? | * Are all ]s ]? | ||
| Line 1,101: | Line 1,054: | ||
| * Are there infinitely many ]s? | * Are there infinitely many ]s? | ||
| * Are there infinitely many ]s? | * Are there infinitely many ]s? | ||
| * Can a prime ''p'' satisfy |
* Can a prime ''p'' satisfy <math>2^{p-1}\equiv 1\pmod{p^2}</math> and <math>3^{p-1}\equiv 1\pmod{p^2}</math> simultaneously?<ref>{{cite arXiv |last=Dobson |first= J. B. |date=1 April 2017 |title=On Lerch's formula for the Fermat quotient |eprint=1103.3907v6|page=23|mode=cs2|class= math.NT }}</ref> | ||
| * Does every prime number appear in the ]? | * Does every prime number appear in the ]? | ||
| * Find the smallest ] | * Find the smallest ] | ||
| Line 1,108: | Line 1,061: | ||
| * For any given integer ''a'' which is not a square and does not equal to −1, are there infinitely many primes with ''a'' as a primitive root? | * For any given integer ''a'' which is not a square and does not equal to −1, are there infinitely many primes with ''a'' as a primitive root? | ||
| * For any given integer ''b'' which is not a perfect power and not of the form −4''k''<sup>4</sup> for integer ''k'', are there infinitely many ] primes to base ''b''? | * For any given integer ''b'' which is not a perfect power and not of the form −4''k''<sup>4</sup> for integer ''k'', are there infinitely many ] primes to base ''b''? | ||
| * For any given integers |
* For any given integers <math>k\geq 1, b\geq 2, c\neq 0</math>, with {{nowrap|1=gcd(''k'', ''c'') = 1}} and {{nowrap|1=gcd(''b'', ''c'') = 1,}} are there infinitely many primes of the form <math>(k\times b^n+c)/\text{gcd}(k+c,b-1)</math> with integer ''n'' ≥ 1? | ||
| * Is every ] |
* Is every ] <math>2^{2^n} + 1</math> composite for <math>n > 4</math>? | ||
| * Is 509,203 the lowest ]? | * Is 509,203 the lowest ]? | ||
| Line 1,116: | Line 1,069: | ||
| Note: These conjectures are about ] of ] with ], and may not be able to be expressed in models of other set theories such as the various ] or ]. | Note: These conjectures are about ] of ] with ], and may not be able to be expressed in models of other set theories such as the various ] or ]. | ||
| ====Conjectures, problems, and hypotheses==== | |||
| * (]) Does the ] below a ] imply the ] everywhere? | * (]) Does the ] below a ] imply the ] everywhere? | ||
| * Does the ] entail ] for every ] <math>\lambda</math>? | * Does the ] entail ] for every ] <math>\lambda</math>? | ||
| * Does the ] imply the existence of an ]? | * Does the ] imply the existence of an ]? | ||
| * If ℵ<sub>ω</sub> is a strong limit cardinal, |
* If ℵ<sub>ω</sub> is a strong limit cardinal, is <math>2^{\aleph_\omega} < \aleph_{\omega_1}</math> (see ])? The best bound, ℵ<sub>ω<sub>4</sub></sub>, was obtained by ] using his ]. | ||
| * The problem of finding the ultimate ], one that contains all ]. | * The problem of finding the ultimate ], one that contains all ]. | ||
| * ] ] |
* ] ]: if there is a ] of ]s, then ] satisfies an analogue of ]. | ||
| ====Open questions==== | |||
| * Does the ] of the existence of a ] imply the consistent existence of a ]? | * Does the ] of the existence of a ] imply the consistent existence of a ]? | ||
| * Does there exist a ] on ℵ<sub>ω</sub>? | * Does there exist a ] on ℵ<sub>ω</sub>? | ||
| Line 1,134: | Line 1,084: | ||
| {{Main|Topology}} | {{Main|Topology}} | ||
| ] asks whether there is an efficient algorithm to identify when the shape presented in a ] is actually the ].]] | ] asks whether there is an efficient algorithm to identify when the shape presented in a ] is actually the ].]] | ||
| * ]: the ] is an ]. | |||
| ====Conjectures and problems==== | |||
| * ]: every <math>n</math>-dimensional ] ] is a ]. | |||
| * ] that the ] is an ]. | |||
| * ] |
* ]: ] ]s are determined up to ] by their ]s. | ||
| * ] that ] ]s are determined up to ] by their ]s. | |||
| * ] on rational ]s of certain ]s. | * ] on rational ]s of certain ]s. | ||
| * ] |
* ]: if a ] ] has a ], ] on a ], then the group must be a ]. | ||
| * Mazur's conjectures<ref>{{citation |last=Mazur |first=Barry |author-link=Barry Mazur |title=The topology of rational points |journal=] |volume=1 |number=1 |year=1992 |pages=35–45 |doi=10.1080/10586458.1992.10504244 |s2cid=17372107 |url=https://projecteuclid.org/euclid.em/1048709114 |access-date=2019-04-07 |archive-url=https://web.archive.org/web/20190407161124/https://projecteuclid.org/euclid.em/1048709114 |archive-date=2019-04-07 |url-status=live }}</ref> | * Mazur's conjectures<ref>{{citation |last=Mazur |first=Barry |author-link=Barry Mazur |title=The topology of rational points |journal=] |volume=1 |number=1 |year=1992 |pages=35–45 |doi=10.1080/10586458.1992.10504244 |s2cid=17372107 |url=https://projecteuclid.org/euclid.em/1048709114 |access-date=2019-04-07 |archive-url=https://web.archive.org/web/20190407161124/https://projecteuclid.org/euclid.em/1048709114 |archive-date=2019-04-07 |url-status=live }}</ref> | ||
| * ] on the ] of certain ]s in the ]es of a ], arising from the ]. | * ] on the ] of certain ]s in the ]es of a ], arising from the ]. | ||
| Line 1,155: | Line 1,104: | ||
| * ]: can ]s be recognized in ]? | * ]: can ]s be recognized in ]? | ||
| * ] relating ]s of ] to the ] of their ]s. | * ] relating ]s of ] to the ] of their ]s. | ||
| * ] |
* ]: every ] ] of a two-dimensional ] ] is aspherical. | ||
| * ]: given a finite ] two-dimensional ] <math>K</math>, is the space <math>K \times </math> ]? | * ]: given a finite ] two-dimensional ] <math>K</math>, is the space <math>K \times </math> ]? | ||
| == Problems solved since 1995 == | == Problems solved since 1995 == | ||
| ], here illustrated with a 2D manifold, was the key tool in ]'s ].]] | {{Duplication|date=August 2022|section=y}}], here illustrated with a 2D manifold, was the key tool in ]'s ].]] | ||
| ===Analysis=== | ===Analysis=== | ||
| Line 1,395: | Line 1,344: | ||
| ====20th century==== | ====20th century==== | ||
| * ] (], 1998)<ref>{{Citation | last1=Lafforgue | first1=Laurent | title=Chtoucas de Drinfeld et applications | language=fr | trans-title=Drinfelʹd shtukas and applications | url=http://www.math.uni-bielefeld.de/documenta/xvol-icm/07/Lafforgue.MAN.html | mr=1648105 | year=1998 | journal=Documenta Mathematica | issn=1431-0635 | volume=II | pages=563–570 | access-date=2016-03-18 | archive-url=https://web.archive.org/web/20180427200241/https://www.math.uni-bielefeld.de/documenta/xvol-icm/07/Lafforgue.MAN.html | archive-date=2018-04-27 | url-status=live }}</ref> | * ] (], 1998)<ref>{{Citation | last1=Lafforgue | first1=Laurent | title=Chtoucas de Drinfeld et applications | language=fr | trans-title=Drinfelʹd shtukas and applications | url=http://www.math.uni-bielefeld.de/documenta/xvol-icm/07/Lafforgue.MAN.html | mr=1648105 | year=1998 | journal=Documenta Mathematica | issn=1431-0635 | volume=II | pages=563–570 | access-date=2016-03-18 | archive-url=https://web.archive.org/web/20180427200241/https://www.math.uni-bielefeld.de/documenta/xvol-icm/07/Lafforgue.MAN.html | archive-date=2018-04-27 | url-status=live }}</ref> | ||
| * ] (] and ], 1995)<ref>{{cite journal|last=Wiles|first=Andrew|author-link=Andrew Wiles|year=1995|title=Modular elliptic curves and Fermat's Last Theorem|url=http://math.stanford.edu/~lekheng/flt/wiles.pdf|journal=Annals of Mathematics|volume=141|issue=3|pages=443–551|oclc=37032255|doi=10.2307/2118559|jstor=2118559|citeseerx=10.1.1.169.9076|access-date=2016-03-06|archive-url=https://web.archive.org/web/20110510062158/http://math.stanford.edu/%7Elekheng/flt/wiles.pdf|archive-date=2011-05-10|url-status=live}}</ref><ref>{{cite journal |author |
* ] (] and ], 1995)<ref>{{cite journal|last=Wiles|first=Andrew|author-link=Andrew Wiles|year=1995|title=Modular elliptic curves and Fermat's Last Theorem|url=http://math.stanford.edu/~lekheng/flt/wiles.pdf|journal=Annals of Mathematics|volume=141|issue=3|pages=443–551|oclc=37032255|doi=10.2307/2118559|jstor=2118559|citeseerx=10.1.1.169.9076|access-date=2016-03-06|archive-url=https://web.archive.org/web/20110510062158/http://math.stanford.edu/%7Elekheng/flt/wiles.pdf|archive-date=2011-05-10|url-status=live}}</ref><ref>{{cite journal |author=], ] |year=1995 |title=Ring theoretic properties of certain Hecke algebras |url=http://www.math.harvard.edu/~rtaylor/hecke.ps |url-status=dead |journal=Annals of Mathematics |volume=141 |issue=3 |pages=553–572 |citeseerx=10.1.1.128.531 |doi=10.2307/2118560 |jstor=2118560 |oclc=37032255 |archive-url=https://web.archive.org/web/20000916161311/http://www.math.harvard.edu/~rtaylor/hecke.ps |archive-date=16 September 2000}}</ref> | ||
| ===Ramsey theory=== | ===Ramsey theory=== | ||
| Line 1,419: | Line 1,368: | ||
| ===Theoretical computer science=== | ===Theoretical computer science=== | ||
| *] for Boolean functions (], 2019) |
*] for Boolean functions (], 2019)<ref>{{cite web | ||
| | url = https://www.popularmechanics.com/science/math/g30346822/biggest-math-breakthroughs-2019/ | | url = https://www.popularmechanics.com/science/math/g30346822/biggest-math-breakthroughs-2019/ | ||
| |author =Linkletter, David | |author =Linkletter, David | ||
| Line 1,431: | Line 1,380: | ||
| ===Topology=== | ===Topology=== | ||
| *Deciding whether the ] is a ] (], 2020)<ref> |
*Deciding whether the ] is a ] (], 2020)<ref>{{Cite journal |last=Piccirillo |first=Lisa |date=2020 |title=The Conway knot is not slice |url=https://annals.math.princeton.edu/2020/191-2/p05 |journal=] |volume=191 |pages=581–591 |doi=10.4007/annals.2020.191.2.5}}</ref><ref>{{Cite web |last=Klarreich |first=Erica |author-link=Erica Klarreich |date=2020-05-19 |title=Graduate Student Solves Decades-Old Conway Knot Problem |url=https://www.quantamagazine.org/graduate-student-solves-decades-old-conway-knot-problem-20200519/ |access-date=2022-08-17 |website=] |language=en}}</ref> | ||
| * ] (], Daniel Groves, Jason Manning, 2012)<ref>{{Cite journal | * ] (], Daniel Groves, Jason Manning, 2012)<ref>{{Cite journal | ||
| | arxiv = 1204.2810v1 | | arxiv = 1204.2810v1 | ||
| Line 1,494: | Line 1,443: | ||
| | date=2015 | | date=2015 | ||
| | doi=10.4007/annals.2015.182.3.5 | doi-access=free}}</ref> | | doi=10.4007/annals.2015.182.3.5 | doi-access=free}}</ref> | ||
| * ] (], 2014)<ref>{{Cite magazine |date=March 28, 2017 |title=A Long-Sought Proof, Found and Almost Lost |url=https://www.quantamagazine.org/20170328-statistician-proves-gaussian-correlation-inequality/ | |
* ] (], 2014)<ref>{{Cite magazine |last=Wolchover |first=Natalie |date=March 28, 2017 |title=A Long-Sought Proof, Found and Almost Lost |url=https://www.quantamagazine.org/20170328-statistician-proves-gaussian-correlation-inequality/ |url-status=live |magazine=] |publisher= |archive-url=https://web.archive.org/web/20170424133433/https://www.quantamagazine.org/20170328-statistician-proves-gaussian-correlation-inequality/ |archive-date=April 24, 2017 |access-date=May 2, 2017}}</ref> | ||
| * Beck's conjecture on discrepancies of set systems constructed from three permutations (Alantha Newman, ], 2011)<ref>{{Cite arXiv |eprint = 1104.2922|last1=Newman |first1=Alantha | last2=Nikolov | first2=Aleksandar |title = A counterexample to Beck's conjecture on the discrepancy of three permutations|class = cs.DM|year = 2011}}</ref> | * Beck's conjecture on discrepancies of set systems constructed from three permutations (Alantha Newman, ], 2011)<ref>{{Cite arXiv |eprint = 1104.2922|last1=Newman |first1=Alantha | last2=Nikolov | first2=Aleksandar |title = A counterexample to Beck's conjecture on the discrepancy of three permutations|class = cs.DM|year = 2011}}</ref> | ||
| * ] (], 2011)<ref>{{Cite web |url=https://annals.math.princeton.edu/wp-content/uploads/annals-v174-n1-p11-p.pdf |title=On motivic cohomology with Z/''l''-coefficients |last=Voevodsky |first=Vladimir |access-date=2016-03-18 |archive-url=https://web.archive.org/web/20160327035457/http://annals.math.princeton.edu/wp-content/uploads/annals-v174-n1-p11-p.pdf |location=School of Mathematics Institute for Advanced Study Einstein Drive Princeton, NJ 08540|publisher=annals.math.princeton.edu (])|date=1 July 2011|volume=174|issue=1|pages=401–438|archive-date=2016-03-27 |url-status=live }}</ref> (and ] and by work of ] and ] (2001) also ]<ref>{{cite journal | * ] (], 2011)<ref>{{Cite web |url=https://annals.math.princeton.edu/wp-content/uploads/annals-v174-n1-p11-p.pdf |title=On motivic cohomology with Z/''l''-coefficients |last=Voevodsky |first=Vladimir |access-date=2016-03-18 |archive-url=https://web.archive.org/web/20160327035457/http://annals.math.princeton.edu/wp-content/uploads/annals-v174-n1-p11-p.pdf |location=School of Mathematics Institute for Advanced Study Einstein Drive Princeton, NJ 08540|publisher=annals.math.princeton.edu (])|date=1 July 2011|volume=174|issue=1|pages=401–438|archive-date=2016-03-27 |url-status=live }}</ref> (and ] and by work of ] and ] (2001) also ]<ref>{{cite journal | ||
| Line 1,506: | Line 1,455: | ||
| | volume = 2001 | | volume = 2001 | ||
| | year = 2001| issue = 530 | | year = 2001| issue = 530 | ||
| }}</ref><ref>{{cite web|url=https://webusers.imj-prg.fr/~bruno.kahn/preprints/kcag.pdf |
}}</ref><ref>{{cite web |last=Kahn |first=Bruno |title=Algebraic K-Theory, Algebraic Cycles and Arithmetic Geometry |url=https://webusers.imj-prg.fr/~bruno.kahn/preprints/kcag.pdf |url-status=live |archive-url=https://web.archive.org/web/20160327035553/https://webusers.imj-prg.fr/~bruno.kahn/preprints/kcag.pdf |archive-date=2016-03-27 |access-date=2016-03-18 |website=webusers.imj-prg.fr}}</ref>{{Rp|page=359}}<ref>{{cite web|url=https://mathoverflow.net/q/87162 |title=motivic cohomology – Milnor–Bloch–Kato conjecture implies the Beilinson-Lichtenbaum conjecture – MathOverflow|access-date=2016-03-18 }}</ref>) | ||
| =====2000s===== | =====2000s===== | ||
| Line 1,666: | Line 1,615: | ||
| * | * | ||
| * | * | ||
| * |
* | ||
| * | * | ||
| * . MathPro Press. | * . MathPro Press. | ||
Revision as of 02:05, 17 August 2022
List article of unsolved mathematical problems This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources.Many mathematical problems have been stated but not yet solved. These problems come from many areas of mathematics, such as theoretical physics, computer science, algebra, analysis, combinatorics, algebraic, differential, discrete and Euclidean geometries, graph theory, group theory, model theory, number theory, set theory, Ramsey theory, dynamical systems, and partial differential equations. Some problems belong to more than one discipline and are studied using techniques from different areas. Prizes are often awarded for the solution to a long-standing problem, and some lists of unsolved problems, such as the Millennium Prize Problems, receive considerable attention.
This list is a composite of notable unsolved problems mentioned in previously published lists, including but not limited to lists considered authoritative. Although this list may never be comprehensive, the problems listed here vary widely in both difficulty and importance.
Lists of unsolved problems in mathematics
Various mathematicians and organizations have published and promoted lists of unsolved mathematical problems. In some cases, the lists have been associated with prizes for the discoverers of solutions.
| List | Number of problems |
Number unsolved or incompletely solved |
Proposed by | Proposed in |
|---|---|---|---|---|
| Hilbert's problems | 23 | 15 | David Hilbert | 1900 |
| Landau's problems | 4 | 4 | Edmund Landau | 1912 |
| Taniyama's problems | 36 | - | Yutaka Taniyama | 1955 |
| Thurston's 24 questions | 24 | - | William Thurston | 1982 |
| Smale's problems | 18 | 14 | Stephen Smale | 1998 |
| Millennium Prize Problems | 7 | 6 | Clay Mathematics Institute | 2000 |
| Simon problems | 15 | <12 | Barry Simon | 2000 |
| Unsolved Problems on Mathematics for the 21st Century | 22 | - | Jair Minoro Abe, Shotaro Tanaka | 2001 |
| DARPA's math challenges | 23 | - | DARPA | 2007 |
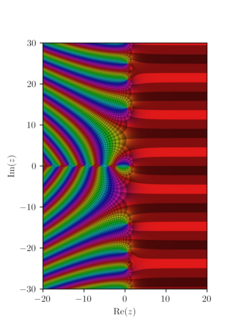
Millennium Prize Problems
Of the original seven Millennium Prize Problems set by the Clay Mathematics Institute in 2000, six remain unsolved:
- Birch and Swinnerton-Dyer conjecture
- Hodge conjecture
- Navier–Stokes existence and smoothness
- P versus NP
- Riemann hypothesis
- Yang–Mills existence and mass gap
The seventh problem, the Poincaré conjecture, was solved by Grigori Perelman in 2003. However, a generalization called the smooth four-dimensional Poincaré conjecture—that is, whether a four-dimensional topological sphere can have two or more inequivalent smooth structures—is unsolved.
Unsolved problems
Algebra
Main article: Algebra
- Birch–Tate conjecture on the relation between the order of the center of the Steinberg group of the ring of integers of a number field to the field's Dedekind zeta function.
- Bombieri–Lang conjectures on densities of rational points of algebraic surfaces and algebraic varieties defined on number fields and their field extensions.
- Connes embedding problem in Von Neumann algebra theory
- Crouzeix's conjecture: the matrix norm of a complex function applied to a complex matrix is at most twice the supremum of over the field of values of .
- Demazure conjecture on representations of algebraic groups over the integers.
- Eilenberg–Ganea conjecture: a group with cohomological dimension 2 also has a 2-dimensional Eilenberg–MacLane space .
- Farrell–Jones conjecture on whether certain assembly maps are isomorphisms.
- Bost conjecture. a specific case of the Farrell–Jones conjecture
- Finite lattice representation problem: is every finite lattice isomorphic to the congruence lattice of some finite algebra?
- Green's conjecture: the Clifford index of a non-hyperelliptic curve is determined by the extent to which it, as a canonical curve, has linear syzygies.
- Grothendieck–Katz p-curvature conjecture
- Hadamard conjecture: for every positive integer , a Hadamard matrix of order exists.
- Hadamard's maximal determinant problem: what is the largest determinant of a matrix with entries all equal to 1 or –1?
- Hilbert's fifteenth problem: put Schubert calculus on a rigorous foundation.
- Hilbert's sixteenth problem: what are the possible configurations of the connected components of M-curves?
- Homological conjectures in commutative algebra
- Jacobson's conjecture: the intersection of all powers of the Jacobson radical of a left-and-right Noetherian ring is precisely 0.
- Kaplansky's conjectures
- Köthe conjecture: if a ring has no nil ideal other than , then it has no nil one-sided ideal other than .
- Existence of perfect cuboids and associated cuboid conjectures
- Pierce–Birkhoff conjecture: every piecewise-polynomial is the maximum of a finite set of minimums of finite collections of polynomials.
- Rota's basis conjecture: for matroids of rank with disjoint bases , it is possible to create an matrix whose rows are and whose columns are also bases.
- Sendov's conjecture: if a complex polynomial with degree at least has all roots in the closed unit disk, then each root is within distance from some critical point.
- Serre's conjecture II: if is a simply connected semisimple algebraic group over a perfect field of cohomological dimension at most , then the Galois cohomology set is zero.
- Serre's multiplicity conjectures
- Uniform boundedness conjecture for rational points: do algebraic curves of genus over number fields have at most some bounded number of -rational points?
- Wild problem: classification of pairs of matrices under simultaneous conjugation and problems containing it such as a lot of classification problems
- Zariski–Lipman conjecture: for a complex algebraic variety with coordinate ring , if the derivations of are a free module over , then is smooth.
- Zauner's conjecture: do SIC-POVMs exist in all dimensions?
Notebook problems
- The Dniester Notebook (Template:Lang-ru) lists several hundred unsolved problems in algebra, particularly ring theory and modulus theory.
- The Erlagol Notebook (Template:Lang-ru) lists unsolved problems in algebra and model theory.
Analysis
Main article: Mathematical analysis
- The Brennan conjecture: estimating the integral of powers of the moduli of the derivative of conformal maps into the open unit disk, on certain subsets of
- The four exponentials conjecture: the transcendence of at least one of four exponentials of combinations of irrationals
- Goodman's conjecture on the coefficients of multivalent functions
- Invariant subspace problem – does every bounded operator on a complex Banach space send some non-trivial closed subspace to itself?
- Kung–Traub conjecture on the optimal order of a multipoint iteration without memory
- Lehmer's conjecture on the Mahler measure of non-cyclotomic polynomials
- The Pompeiu problem on the topology of domains for which some nonzero function has integrals that vanish over every congruent copy
- Schanuel's conjecture on the transcendence degree of exponentials of linearly independent irrationals
- Vitushkin's conjecture on compact subsets of with analytic capacity
- Are (the Euler–Mascheroni constant),, Catalan's constant, or Khinchin's constant rational, algebraic irrational, or transcendental? What is the irrationality measure of each of these numbers?
- What is the exact value of Landau's constants, including Bloch's constant?
- How are suspended infinite-infinitesimals paradoxes justified?
- Regularity of solutions of Euler equations
- Convergence of Flint Hills series
- Regularity of solutions of Vlasov–Maxwell equations
Combinatorics
Main article: Combinatorics- The 1/3–2/3 conjecture – does every finite partially ordered set that is not totally ordered contain two elements x and y such that the probability that x appears before y in a random linear extension is between 1/3 and 2/3?
- Problems in Latin squares – Open questions concerning Latin squares
- The lonely runner conjecture – if runners with pairwise distinct speeds run round a track of unit length, will every runner be "lonely" (that is, be at least a distance from each other runner) at some time?
- The sunflower conjecture: can the number of size sets required for the existence of a sunflower of sets be bounded by an exponential function in for every fixed ?
- No-three-in-line problem – how many points can be placed in the grid so that no three of them lie on a line?
- Frankl's union-closed sets conjecture – for any family of sets closed under sums there exists an element (of the underlying space) belonging to half or more of the sets
- The values of the Dedekind numbers for .
- Give a combinatorial interpretation of the Kronecker coefficients.
- The values of the Ramsey numbers, particularly
- Finding a function to model n-step self-avoiding walks.
- The values of the Van der Waerden numbers
Dynamical systems
Main article: Dynamical system
- Arnold–Givental conjecture and Arnold conjecture – relating symplectic geometry to Morse theory
- Quantum chaos: Berry–Tabor conjecture
- Banach's problem – is there an ergodic system with simple Lebesgue spectrum?
- Birkhoff conjecture – if a billiard table is strictly convex and integrable, is its boundary necessarily an ellipse?
- Collatz conjecture (aka the conjecture)
- Eremenko's conjecture: every component of the escaping set of an entire transcendental function is unbounded
- Furstenberg conjecture – is every invariant and ergodic measure for the action on the circle either Lebesgue or atomic?
- Kaplan–Yorke conjecture on the dimension of an attractor in terms of its Lyapunov exponents
- Margulis conjecture – measure classification for diagonalizable actions in higher-rank groups
- MLC conjecture – is the Mandelbrot set locally connected?
- Many problems concerning an outer billiard, for example showing that outer billiards relative to almost every convex polygon have unbounded orbits.
- Quantum unique ergodicity conjecture on the distribution of large-frequency eigenfunctions of the Laplacian on a negatively-curved manifold
- Rokhlin's multiple mixing problem – are all strongly mixing systems also strongly 3-mixing?
- Weinstein conjecture – does a regular compact contact type level set of a Hamiltonian on a symplectic manifold carry at least one periodic orbit of the Hamiltonian flow?
- Does every positive integer generate a juggler sequence terminating at 1?
- Lyapunov function: Lyapunov's second method for stability – For what classes of ODEs, describing dynamical systems, does the Lyapunov’s second method formulated in the classical and canonically generalized forms define the necessary and sufficient conditions for the (asymptotical) stability of motion?
- Is every reversible cellular automaton in three or more dimensions locally reversible?
Games and puzzles
Main article: Game theoryCombinatorial games
Main article: Combinatorial game theory- Is there a non-terminating game of beggar-my-neighbour?
- Sudoku:
- How many puzzles have exactly one solution?
- How many puzzles with exactly one solution are minimal?
- What is the maximum number of givens for a minimal puzzle?
- How many puzzles have exactly one solution?
- Tic-tac-toe variants:
- Given a width of tic-tac-toe board, what is the smallest dimension such that X is guaranteed a winning strategy?
- What is the Turing completeness status of all unique elementary cellular automata?
Games with imperfect information
Geometry
Main article: GeometryAlgebraic geometry
Main article: Algebraic geometry- Abundance conjecture: if the canonical bundle of a projective variety with Kawamata log terminal singularities is nef, then it is semiample.
- Bass conjecture on the finite generation of certain algebraic K-groups.
- Deligne conjecture: any one of numerous named for Pierre Deligne.
- Dixmier conjecture: any endomorphism of a Weyl algebra is an automorphism.
- Fröberg conjecture on the Hilbert functions of a set of forms.
- Fujita conjecture regarding the line bundle constructed from a positive holomorphic line bundle on a compact complex manifold and the canonical line bundle of
- Hartshorne's conjectures
- Jacobian conjecture: if a polynomial mapping over a characteristic-0 field has a constant nonzero Jacobian determinant, then it has a regular (i.e. with polynomial components) inverse function.
- Manin conjecture on the distribution of rational points of bounded height in certain subsets of Fano varieties
- Maulik–Nekrasov–Okounkov–Pandharipande conjecture on an equivalence between Gromov–Witten theory and Donaldson–Thomas theory
- Nakai conjecture: if a complex algebraic variety has a ring of differential operators generated by its contained derivations, then it must be smooth.
- Parshin's conjecture: the higher algebraic K-groups of any smooth projective variety defined over a finite field must vanish up to torsion.
- Section conjecture on splittings of group homomorphisms from fundamental groups of complete smooth curves over finitely-generated fields to the Galois group of .
- Standard conjectures on algebraic cycles
- Tate conjecture on the connection between algebraic cycles on algebraic varieties and Galois representations on étale cohomology groups.
- Virasoro conjecture: a certain generating function encoding the Gromov–Witten invariants of a smooth projective variety is fixed by an action of half of the Virasoro algebra.
- Zariski multiplicity conjecture on the topological equisingularity and equimultiplicity of varieties at singular points
- Are infinite sequences of flips possible in dimensions greater than 3?
- Resolution of singularities in characteristic
Covering and packing
- Borsuk's problem on upper and lower bounds for the number of smaller-diameter subsets needed to cover a bounded n-dimensional set.
- The covering problem of Rado: if the union of finitely many axis-parallel squares has unit area, how small can the largest area covered by a disjoint subset of squares be?
- The Erdős–Oler conjecture: when is a triangular number, packing circles in an equilateral triangle requires a triangle of the same size as packing circles
- The kissing number problem for dimensions other than 1, 2, 3, 4, 8 and 24
- Reinhardt's conjecture: the smoothed octagon has the lowest maximum packing density of all centrally-symmetric convex plane sets
- Sphere packing problems, including the density of the densest packing in dimensions other than 1, 2, 3, 8 and 24, and its asymptotic behavior for high dimensions.
- Square packing in a square: what is the asymptotic growth rate of wasted space?
- Ulam's packing conjecture about the identity of the worst-packing convex solid
Differential geometry
Main article: Differential geometry- The spherical Bernstein's problem, a generalization of Bernstein's problem
- Carathéodory conjecture: any convex, closed, and twice-differentiable surface in three-dimensional Euclidean space admits at least two umbilical points
- Cartan–Hadamard conjecture: Can the classical isoperimetric inequality for subsets of Euclidean space be extended to spaces of nonpositive curvature, known as Cartan–Hadamard manifolds?
- Chern's conjecture (affine geometry) that the Euler characteristic of a compact affine manifold vanishes.
- Chern's conjecture for hypersurfaces in spheres, a number of closely-related conjectures.
- Closed curve problem: Find (explicit) necessary and sufficient conditions that determine when, given two periodic functions with the same period, the integral curve is closed.
- The filling area conjecture, that a hemisphere has the minimum area among shortcut-free surfaces in Euclidean space whose boundary forms a closed curve of given length
- The Hopf conjectures relating the curvature and Euler characteristic of higher-dimensional Riemannian manifolds
- Yau's conjecture: a closed Riemannian 3-manifold has an infinite number of smooth closed immersed minimal surfaces.
- Yau's conjecture on the first eigenvalue that the first eigenvalue for the Laplace–Beltrami operator on an embedded minimal hypersurface of is .
Discrete geometry
Main article: Discrete geometry
- The Hadwiger conjecture on covering n-dimensional convex bodies with at most 2 smaller copies
- Solving the happy ending problem for arbitrary
- Improving lower and upper bounds for the Heilbronn triangle problem.
- Kalai's 3 conjecture on the least possible number of faces of centrally symmetric polytopes.
- The Kobon triangle problem on triangles in line arrangements
- The Kusner conjecture: at most points can be equidistant in spaces
- The McMullen problem on projectively transforming sets of points into convex position
- Opaque forest problem on finding opaque sets for various planar shapes
- How many unit distances can be determined by a set of n points in the Euclidean plane?
- Finding matching upper and lower bounds for k-sets and halving lines
- Tripod packing: how many tripods can have their apexes packed into a given cube?
Euclidean geometry
Main article: Euclidean geometry- The Atiyah conjecture on configurations on the invertibility of a certain -by- matrix depending on points in
- Bellman's lost in a forest problem – find the shortest route that is guaranteed to reach the boundary of a given shape, starting at an unknown point of the shape with unknown orientation
- Danzer's problem and Conway's dead fly problem – do Danzer sets of bounded density or bounded separation exist?
- Ehrhart's volume conjecture: a convex body in dimensions containing a single lattice point in its interior as its center of mass cannot have volume greater than
- The einstein problem – does there exist a two-dimensional shape that forms the prototile for an aperiodic tiling, but not for any periodic tiling?
- Falconer's conjecture: sets of Hausdorff dimension greater than in must have a distance set of nonzero Lebesgue measure
- Inscribed square problem, also known as Toeplitz' conjecture and the square peg problem – does every Jordan curve have an inscribed square?
- The Kakeya conjecture – do -dimensional sets that contain a unit line segment in every direction necessarily have Hausdorff dimension and Minkowski dimension equal to ?
- The Kelvin problem on minimum-surface-area partitions of space into equal-volume cells, and the optimality of the Weaire–Phelan structure as a solution to the Kelvin problem
- Lebesgue's universal covering problem on the minimum-area convex shape in the plane that can cover any shape of diameter one
- Mahler's conjecture on the product of the volumes of a centrally symmetric convex body and its polar.
- Moser's worm problem – what is the smallest area of a shape that can cover every unit-length curve in the plane?
- The moving sofa problem – what is the largest area of a shape that can be maneuvered through a unit-width L-shaped corridor?
- Does every convex polyhedron have Rupert's property?
- Shephard's problem (a.k.a. Dürer's conjecture) – does every convex polyhedron have a net, or simple edge-unfolding?
- Is there a non-convex polyhedron without self-intersections with more than seven faces, all of which share an edge with each other?
- The Thomson problem – what is the minimum energy configuration of mutually-repelling particles on a unit sphere?
- Borromean rings — are there three unknotted space curves, not all three circles, which cannot be arranged to form this link?
- Dissection into orthoschemes – is it possible for simplices of every dimension?
- Uniform 5-polytopes – find and classify the complete set of these shapes
Graph theory
Main article: Graph theoryGraph coloring and labeling

- Cereceda's conjecture on the diameter of the space of colorings of degenerate graphs
- The Erdős–Faber–Lovász conjecture on coloring unions of cliques
- The Gyárfás–Sumner conjecture on χ-boundedness of graphs with a forbidden induced tree
- The Hadwiger conjecture relating coloring to clique minors
- The Hadwiger–Nelson problem on the chromatic number of unit distance graphs
- Jaeger's Petersen-coloring conjecture: every bridgeless cubic graph has a cycle-continuous mapping to the Petersen graph
- The list coloring conjecture:, for every graph, the list chromatic index equals the chromatic index
- The total coloring conjecture of Behzad and Vizing that the total chromatic number is at most two plus the maximum degree
Graph drawing
- The Albertson conjecture: the crossing number can be lower-bounded by the crossing number of a complete graph with the same chromatic number
- Conway's thrackle conjecture that thrackles cannot have more edges than vertices
- Harborth's conjecture: every planar graph can be drawn with integer edge lengths
- Negami's conjecture on projective-plane embeddings of graphs with planar covers
- The strong Papadimitriou–Ratajczak conjecture: every polyhedral graph has a convex greedy embedding
- Turán's brick factory problem – Is there a drawing of any complete bipartite graph with fewer crossings than the number given by Zarankiewicz?
- Universal point sets of subquadratic size for planar graphs
Paths and cycles in graphs
- Barnette's conjecture: every cubic bipartite three-connected planar graph has a Hamiltonian cycle
- Chvátal's toughness conjecture, that there is a number t such that every t-tough graph is Hamiltonian
- The cycle double cover conjecture: every bridgeless graph has a family of cycles that includes each edge twice
- The Erdős–Gyárfás conjecture on cycles with power-of-two lengths in cubic graphs
- The linear arboricity conjecture on decomposing graphs into disjoint unions of paths according to their maximum degree
- The Lovász conjecture on Hamiltonian paths in symmetric graphs
- The Oberwolfach problem on which 2-regular graphs have the property that a complete graph on the same number of vertices can be decomposed into edge-disjoint copies of the given graph.
- Szymanski's conjecture: every permutation on the -dimensional doubly-directed hypercube graph can be routed with edge-disjoint paths.
Word-representation of graphs
- Are there any graphs on n vertices whose representation requires more than floor(n/2) copies of each letter?
- Characterise (non-)word-representable planar graphs
- Characterise word-representable graphs in terms of (induced) forbidden subgraphs.
- Characterise word-representable near-triangulations containing the complete graph K4 (such a characterisation is known for K4-free planar graphs)
- Classify graphs with representation number 3, that is, graphs that can be represented using 3 copies of each letter, but cannot be represented using 2 copies of each letter
- Is it true that out of all bipartite graphs, crown graphs require longest word-representants?
- Is the line graph of a non-word-representable graph always non-word-representable?
- Which (hard) problems on graphs can be translated to words representing them and solved on words (efficiently)?
Miscellaneous graph theory
- Babai's problem: which groups are Babai invariant groups?
- Brouwer's conjecture on upper bounds for sums of eigenvalues of Laplacians of graphs in terms of their number of edges.
- Conway's 99-graph problem: does there exist a strongly regular graph with parameters (99,14,1,2)?
- Degree diameter problem: given two positive integers , what is the largest graph of diameter such that all vertices have degrees at most ?
- The Erdős–Hajnal conjecture on large cliques or independent sets in graphs with a forbidden induced subgraph
- The GNRS conjecture on whether minor-closed graph families have embeddings with bounded distortion
- Graham's pebbling conjecture on the pebbling number of Cartesian products of graphs
- The implicit graph conjecture on the existence of implicit representations for slowly-growing hereditary families of graphs
- Jørgensen's conjecture that every 6-vertex-connected K6-minor-free graph is an apex graph
- Meyniel's conjecture that cop number is
- The reconstruction conjecture and new digraph reconstruction conjecture on whether a graph is uniquely determined by its vertex-deleted subgraphs.
- The second neighborhood problem: does every oriented graph contain a vertex for which there are at least as many other vertices at distance two as at distance one?
- Do there exist infinitely many strongly regular geodetic graphs, or any strongly regular geodetic graphs that are not Moore graphs?
- Sumner's conjecture: does every -vertex tournament contain as a subgraph every -vertex oriented tree?
- Tutte's conjectures that every bridgeless graph has a nowhere-zero 5-flow and every Petersen-minor-free bridgeless graph has a nowhere-zero 4-flow
- Vizing's conjecture on the domination number of cartesian products of graphs
- Zarankiewicz problem: how many edges can there be in a bipartite graph on a given number of vertices with no complete bipartite subgraphs of a given size?
- Does a Moore graph with girth 5 and degree 57 exist?
- What is the largest possible pathwidth of an n-vertex cubic graph?
Group theory
Main article: Group theory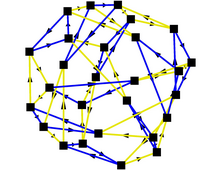
- Andrews–Curtis conjecture: every balanced presentation of the trivial group can be transformed into a trivial presentation by a sequence of Nielsen transformations on relators and conjugations of relators
- Guralnick–Thompson conjecture on the composition factors of groups in genus-0 systems
- Herzog–Schönheim conjecture: if a finite system of left cosets of subgroups of a group form a partition of , then the finite indices of said subgroups cannot be distinct.
- The inverse Galois problem: is every finite group the Galois group of a Galois extension of the rationals?
- Problems in loop theory and quasigroup theory consider generalizations of groups
- Are there an infinite number of Leinster groups?
- Does generalized moonshine exist?
- For which positive integers m, n is the free Burnside group B(m,n) finite? In particular, is B(2, 5) finite?
- Is every finitely presented periodic group finite?
- Is every group surjunctive?
Notebook problems
- The Kourovka Notebook is a collection of unsolved problems in group theory, first published in 1965 and updated many times since.
Model theory and formal languages
Main articles: Model theory and formal languages- The Cherlin–Zilber conjecture: A simple group whose first-order theory is stable in is a simple algebraic group over an algebraically closed field.
- Generalized star height problem: can all regular languages be expressed using generalized regular expressions with limited nesting depths of Kleene stars?
- For which number fields does Hilbert's tenth problem hold?
- Kueker's conjecture
- The main gap conjecture, e.g. for uncountable first order theories, for AECs, and for -saturated models of a countable theory.
- Shelah's categoricity conjecture for : If a sentence is categorical above the Hanf number then it is categorical in all cardinals above the Hanf number.
- Shelah's eventual categoricity conjecture: For every cardinal there exists a cardinal such that if an AEC K with LS(K)<= is categorical in a cardinal above then it is categorical in all cardinals above .
- The stable field conjecture: every infinite field with a stable first-order theory is separably closed.
- The stable forking conjecture for simple theories
- Tarski's exponential function problem: is the theory of the real numbers with the exponential function decidable?
- The universality problem for C-free graphs: For which finite sets C of graphs does the class of C-free countable graphs have a universal member under strong embeddings?
- The universality spectrum problem: Is there a first-order theory whose universality spectrum is minimum?
- Vaught conjecture: the number of countable models of a first-order complete theory in a countable language is either finite, , or .
- Assume K is the class of models of a countable first order theory omitting countably many types. If K has a model of cardinality does it have a model of cardinality continuum?
- Do the Henson graphs have the finite model property?
- Does a finitely presented homogeneous structure for a finite relational language have finitely many reducts?
- Does there exist an o-minimal first order theory with a trans-exponential (rapid growth) function?
- If the class of atomic models of a complete first order theory is categorical in the , is it categorical in every cardinal?
- Is every infinite, minimal field of characteristic zero algebraically closed? (Here, "minimal" means that every definable subset of the structure is finite or co-finite.)
- (BMTO) Is the Borel monadic theory of the real order decidable? (MTWO) Is the monadic theory of well-ordering consistently decidable?
- Is the theory of the field of Laurent series over decidable? of the field of polynomials over ?
- Is there a logic L which satisfies both the Beth property and Δ-interpolation, is compact but does not satisfy the interpolation property?
- Determine the structure of Keisler's order
Number theory
Main page: Category:Unsolved problems in number theory See also: Number theoryGeneral
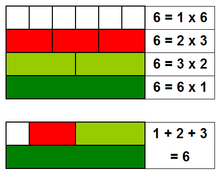
- n conjecture: a generalization of the abc conjecture to more than three integers.
- abc conjecture: for any , is true for only finitely many positive such that .
- Szpiro's conjecture: for any , there is some constant such that, for any elliptic curve defined over with minimal discriminant and conductor , we have .
- Hardy–Littlewood zeta-function conjectures
- Hilbert's eleventh problem: classify quadratic forms over algebraic number fields.
- Hilbert's ninth problem: find the most general reciprocity law for the norm residues of -th order in a general algebraic number field, where is a power of a prime.
- Hilbert's twelfth problem: extend the Kronecker–Weber theorem on Abelian extensions of to any base number field.
- Grand Riemann hypothesis: do the nontrivial zeros of all automorphic L-functions lie on the critical line with real ?
- Generalized Riemann hypothesis: do the nontrivial zeros of all Dirichlet L-functions lie on the critical line with real ?
- Riemann hypothesis: do the nontrivial zeros of the Riemann zeta function lie on the critical line with real ?
- Generalized Riemann hypothesis: do the nontrivial zeros of all Dirichlet L-functions lie on the critical line with real ?
- André–Oort conjecture: is every irreducible component of the Zariski closure of a set of special points in a Shimura variety a special subvariety?
- Beilinson's conjectures
- Brocard's problem: are there any integer solutions to other than ?
- Carmichael's totient function conjecture: do all values of Euler's totient function have multiplicity greater than ?
- Casas-Alvero conjecture: if a polynomial of degree defined over a field of characteristic has a factor in common with its first through -th derivative, then must be the -th power of a linear polynomial?
- Catalan–Dickson conjecture on aliquot sequences: no aliquot sequences are infinite but non-repeating.
- Congruent number problem (a corollary to Birch and Swinnerton-Dyer conjecture, per Tunnell's theorem): determine precisely what rational numbers are congruent numbers.
- Erdős–Moser problem: is the only solution to the Erdős–Moser equation?
- Erdős–Straus conjecture: for every , there are positive integers such that .
- Erdős–Ulam problem: is there a dense set of points in the plane all at rational distances from one-another?
- Exponent pair conjecture (Van der Corput's method): for all , the pair is an exponent pair.
- The Gauss circle problem: how far can the number of integer points in a circle centered at the origin be from the area of the circle?
- Goormaghtigh conjecture on solutions to where and .
- Grimm's conjecture: each element of a set of consecutive composite numbers can be assigned a distinct prime number that divides it.
- Hall's conjecture: for any , there is some constant such that either or .
- Hilbert–Pólya conjecture: the nontrivial zeros of the Riemann zeta function correspond to eigenvalues of a self-adjoint operator.
- Keating–Snaith conjecture concerning the asymptotics of an integral involving the Riemann zeta function
- Lehmer's totient problem: if divides , must be prime?
- Leopoldt's conjecture: a p-adic analogue of the regulator of an algebraic number field does not vanish.
- Lindelöf hypothesis that for all ,
- The density hypothesis for zeroes of the Riemann zeta function
- Littlewood conjecture: for any two real numbers , , where is the distance from to the nearest integer.
- Mahler's 3/2 problem that no real number has the property that the fractional parts of are less than for all positive integers .
- Montgomery's pair correlation conjecture: the normalized pair correlation function between pairs of zeros of the Riemann zeta function is the same as the pair correlation function of random Hermitian matrices.
- Newman's conjecture: the partition function satisfies any arbitrary congruence infinitely often.
- Pillai's conjecture: for any , the equation has finitely many solutions when are not both .
- Piltz divisor problem on bounding
- Dirichlet's divisor problem: the specific case of the Piltz divisor problem for
- Ramanujan–Petersson conjecture: a number of related conjectures that are generalizations of the original conjecture.
- Sato–Tate conjecture: also a number of related conjectures that are generalizations of the original conjecture.
- Scholz conjecture: the length of the shortest addition chain producing is at most plus the length of the shortest addition chain producing .
- Do Siegel zeros exist?
- Singmaster's conjecture: is there a finite upper bound on the multiplicities of the entries greater than 1 in Pascal's triangle?
- The uniqueness conjecture for Markov numbers that every Markov number is the largest number in exactly one normalized solution to the Markov Diophantine equation.
- Vojta's conjecture on heights of points on algebraic varieties over algebraic number fields.
- Are there infinitely many perfect numbers?
- Do any odd perfect numbers exist?
- Do quasiperfect numbers exist?
- Do any non-power of 2 almost perfect numbers exist?
- Are there 65, 66, or 67 idoneal numbers?
- Are there any pairs of amicable numbers which have opposite parity?
- Are there any pairs of betrothed numbers which have same parity?
- Are there any pairs of relatively prime amicable numbers?
- Are there infinitely many amicable numbers?
- Are there infinitely many betrothed numbers?
- Are there infinitely many Giuga numbers?
- Does every rational number with an odd denominator have an odd greedy expansion?
- Do any Lychrel numbers exist?
- Do any odd noncototients exist?
- Do any odd weird numbers exist?
- Do any Taxicab(5, 2, n) exist for n > 1?
- Is there a covering system with odd distinct moduli?
- Is a normal number (i.e., is each digit 0–9 equally frequent)?
- Is 10 a solitary number?
- Can a 3×3 magic square be constructed from 9 distinct perfect square numbers?
- Which integers can be written as the sum of three perfect cubes?
- Can every integer be written as a sum of four perfect cubes?
- Find the value of the De Bruijn–Newman constant.
Additive number theory
Main article: Additive number theory See also: Problems involving arithmetic progressions- Beal's conjecture: for all integral solutions to where , all three numbers must share some prime factor.
- Erdős conjecture on arithmetic progressions that if the sum of the reciprocals of the members of a set of positive integers diverges, then the set contains arbitrarily long arithmetic progressions.
- Erdős–Turán conjecture on additive bases that if is an additive basis of order , then the number of ways that positive integers can be expressed as the sum of two numbers in must tend to infinity as tends to infinity.
- Fermat–Catalan conjecture: there are finitely many distinct solutions to the equation with being positive coprime integers and being positive integers satisfying .
- Gilbreath's conjecture on consecutive applications of the unsigned forward difference operator to the sequence of prime numbers.
- Goldbach's conjecture: every even natural number greater than is the sum of two prime numbers.
- Lander, Parkin, and Selfridge conjecture: if the sum of -th powers of positive integers is equal to a different sum of -th powers of positive integers, then .
- Lemoine's conjecture: all odd integers greater than can be represented as the sum of an odd prime number and an even semiprime.
- Minimum overlap problem of estimating the minimum possible maximum number of times a number appears in the termwise difference of two equally large sets partitioning the set
- Pollock's conjectures
- Skolem problem: can an algorithm determine if a constant-recursive sequence contains a zero?
- The values of g(k) and G(k) in Waring's problem
- Do the Ulam numbers have a positive density?
- Determine growth rate of rk(N) (see Szemerédi's theorem)
Algebraic number theory
Main article: Algebraic number theory- Class number problem: are there infinitely many real quadratic number fields with unique factorization?
- Fontaine–Mazur conjecture: actually numerous conjectures, all proposed by Jean-Marc Fontaine and Barry Mazur.
- Gan–Gross–Prasad conjecture: a restriction problem in representation theory of real or p-adic Lie groups.
- Greenberg's conjectures
- Hermite's problem: is it possible, for any natural number , to assign a sequence of natural numbers to each real number such that the sequence for is eventually periodic if and only if is algebraic of degree ?
- Kummer–Vandiver conjecture: primes do not divide the class number of the maximal real subfield of the -th cyclotomic field.
- Lang and Trotter's conjecture on supersingular primes that the number of supersingular primes less than a constant is within a constant multiple of
- Selberg's 1/4 conjecture: the eigenvalues of the Laplace operator on Maass wave forms of congruence subgroups are at least .
- Stark conjectures (including Brumer–Stark conjecture)
- Characterize all algebraic number fields that have some power basis.
Computational number theory
Main article: Computational number theory- Can integer factorization be done in polynomial time?
Prime numbers
Main article: Prime numbers
Conjectures, problems and hypotheses
- Agoh–Giuga conjecture on the Bernoulli numbers that is prime if and only if
- Artin's conjecture on primitive roots that if an integer is neither a perfect square nor , then it is a primitive root modulo infinitely many prime numbers
- Brocard's conjecture: there are always at least prime numbers between consecutive squares of prime numbers, aside from and .
- Bunyakovsky conjecture: if an integer-coefficient polynomial has a positive leading coefficient, is irreducible over the integers, and has no common factors over all where is a positive integer, then is prime infinitely often.
- Catalan's Mersenne conjecture: some Catalan–Mersenne number is composite and thus all Catalan–Mersenne numbers are composite after some point.
- Dickson's conjecture: for a finite set of linear forms with each , there are infinitely many for which all forms are prime, unless there is some congruence condition preventing it.
- Dubner's conjecture: every number greater than is the sum of two primes which both have twins.
- Elliott–Halberstam conjecture on the distribution of prime numbers in arithmetic progressions.
- Erdős–Mollin–Walsh conjecture: no three consecutive numbers are all powerful.
- Feit–Thompson conjecture: for all distinct prime numbers and , does not divide
- Fortune's conjecture that no Fortunate number is composite.
- The Gaussian moat problem: is it possible to find an infinite sequence of distinct Gaussian prime numbers such that the difference between consecutive numbers in the sequence is bounded?
- Gillies' conjecture on the distribution of prime divisors of Mersenne numbers.
- Goldbach conjecture: all even natural numbers greater than are the sum of two prime numbers.
- Landau's problems
- Problems associated to Linnik's theorem
- New Mersenne conjecture: for any odd natural number , if any two of the three conditions or , is prime, and is prime are true, then the third condition is true.
- Polignac's conjecture: for all positive even numbers , there are infinitely many prime gaps of size .
- Schinzel's hypothesis H that for every finite collection of nonconstant irreducible polynomials over the integers with positive leading coefficients, either there are infinitely many positive integers for which are all primes, or there is some fixed divisor which, for all , divides some .
- Selfridge's conjecture: is 78,557 the lowest Sierpiński number?
- Twin prime conjecture: there are infinitely many twin primes.
- Does the converse of Wolstenholme's theorem hold for all natural numbers?
- Are all Euclid numbers square-free?
- Are all Fermat numbers square-free?
- Are all Mersenne numbers of prime index square-free?
- Are there any composite c satisfying 2 ≡ 1 (mod c)?
- Are there any Wall–Sun–Sun primes?
- Are there any Wieferich primes in base 47?
- Are there infinitely many balanced primes?
- Are there infinitely many Carol primes?
- Are there infinitely many cluster primes?
- Are there infinitely many cousin primes?
- Are there infinitely many Cullen primes?
- Are there infinitely many Euclid primes?
- Are there infinitely many Fibonacci primes?
- Are there infinitely many Kummer primes?
- Are there infinitely many Kynea primes?
- Are there infinitely many Lucas primes?
- Are there infinitely many Mersenne primes (Lenstra–Pomerance–Wagstaff conjecture); equivalently, infinitely many even perfect numbers?
- Are there infinitely many Newman–Shanks–Williams primes?
- Are there infinitely many palindromic primes to every base?
- Are there infinitely many Pell primes?
- Are there infinitely many Pierpont primes?
- Are there infinitely many prime quadruplets?
- Are there infinitely many prime triplets?
- Are there infinitely many regular primes, and if so is their relative density ?
- Are there infinitely many sexy primes?
- Are there infinitely many safe and Sophie Germain primes?
- Are there infinitely many Wagstaff primes?
- Are there infinitely many Wieferich primes?
- Are there infinitely many Wilson primes?
- Are there infinitely many Wolstenholme primes?
- Are there infinitely many Woodall primes?
- Can a prime p satisfy and simultaneously?
- Does every prime number appear in the Euclid–Mullin sequence?
- Find the smallest Skewes' number
- For any given integer a > 0, are there infinitely many Lucas–Wieferich primes associated with the pair (a, −1)? (Specially, when a = 1, this is the Fibonacci-Wieferich primes, and when a = 2, this is the Pell-Wieferich primes)
- For any given integer a > 0, are there infinitely many primes p such that a ≡ 1 (mod p)?
- For any given integer a which is not a square and does not equal to −1, are there infinitely many primes with a as a primitive root?
- For any given integer b which is not a perfect power and not of the form −4k for integer k, are there infinitely many repunit primes to base b?
- For any given integers , with gcd(k, c) = 1 and gcd(b, c) = 1, are there infinitely many primes of the form with integer n ≥ 1?
- Is every Fermat number composite for ?
- Is 509,203 the lowest Riesel number?
Set theory
Main article: Set theoryNote: These conjectures are about models of Zermelo-Frankel set theory with choice, and may not be able to be expressed in models of other set theories such as the various constructive set theories or non-wellfounded set theory.
- (Woodin) Does the generalized continuum hypothesis below a strongly compact cardinal imply the generalized continuum hypothesis everywhere?
- Does the generalized continuum hypothesis entail for every singular cardinal ?
- Does the generalized continuum hypothesis imply the existence of an ℵ2-Suslin tree?
- If ℵω is a strong limit cardinal, is (see Singular cardinals hypothesis)? The best bound, ℵω4, was obtained by Shelah using his PCF theory.
- The problem of finding the ultimate core model, one that contains all large cardinals.
- Woodin's Ω-conjecture: if there is a proper class of Woodin cardinals, then Ω-logic satisfies an analogue of Gödel's completeness theorem.
- Does the consistency of the existence of a strongly compact cardinal imply the consistent existence of a supercompact cardinal?
- Does there exist a Jónsson algebra on ℵω?
- Is OCA (the open coloring axiom) consistent with ?
- Without assuming the axiom of choice, can a nontrivial elementary embedding V→V exist?
Topology
Main article: Topology
- Baum–Connes conjecture: the assembly map is an isomorphism.
- Bing–Borsuk conjecture: every -dimensional homogeneous absolute neighborhood retract is a topological manifold.
- Borel conjecture: aspherical closed manifolds are determined up to homeomorphism by their fundamental groups.
- Halperin conjecture on rational Serre spectral sequences of certain fibrations.
- Hilbert–Smith conjecture: if a locally compact topological group has a continuous, faithful group action on a topological manifold, then the group must be a Lie group.
- Mazur's conjectures
- Novikov conjecture on the homotopy invariance of certain polynomials in the Pontryagin classes of a manifold, arising from the fundamental group.
- Quadrisecants of wild knots: it has been conjectured that wild knots always have infinitely many quadrisecants.
- Telescope conjecture: the last of Ravenel's conjectures in stable homotopy theory to be resolved.
- Unknotting problem: can unknots be recognized in polynomial time?
- Volume conjecture relating quantum invariants of knots to the hyperbolic geometry of their knot complements.
- Whitehead conjecture: every connected subcomplex of a two-dimensional aspherical CW complex is aspherical.
- Zeeman conjecture: given a finite contractible two-dimensional CW complex , is the space collapsible?
Problems solved since 1995
| This section duplicates the scope of other articles. Please discuss this issue and help introduce a summary style to the section by replacing the section with a link and a summary or by splitting the content into a new article. (August 2022) |
Analysis
- Kadison–Singer problem (Adam Marcus, Daniel Spielman and Nikhil Srivastava, 2013) (and the Feichtinger's conjecture, Anderson’s paving conjectures, Weaver’s discrepancy theoretic and conjectures, Bourgain-Tzafriri conjecture and -conjecture)
- Ahlfors measure conjecture (Ian Agol, 2004)
- Gradient conjecture (Krzysztof Kurdyka, Tadeusz Mostowski, Adam Parusinski, 1999)
Combinatorics
- Erdős sumset conjecture (Joel Moreira, Florian Richter, Donald Robertson, 2018)
- McMullen's g-conjecture on the possible numbers of faces of different dimensions in a simplicial sphere (also Grünbaum conjecture, several conjectures of Kühnel) (Karim Adiprasito, 2018)
- Hirsch conjecture (Francisco Santos Leal, 2010)
- Stanley–Wilf conjecture (Gábor Tardos and Adam Marcus, 2004) (and also the Alon–Friedgut conjecture)
- Kemnitz's conjecture (Christian Reiher, 2003, Carlos di Fiore, 2003)
- Cameron–Erdős conjecture (Ben J. Green, 2003, Alexander Sapozhenko, 2003)
Dynamical systems
- Painlevé conjecture (Jinxin Xue, 2014)
Game theory
- The angel problem (Various independent proofs, 2006)
Geometry
21st century
- Yau's conjecture (Antoine Song, 2018)
- Pentagonal tiling (Michaël Rao, 2017)
- Willmore conjecture (Fernando Codá Marques and André Neves, 2012)
- Erdős distinct distances problem (Larry Guth, Nets Hawk Katz, 2011)
- Heterogeneous tiling conjecture (squaring the plane) (Frederick V. Henle and James M. Henle, 2008)
- Tameness conjecture (Ian Agol, 2004)
- Ending lamination theorem (Jeffrey F. Brock, Richard D. Canary, Yair N. Minsky, 2004)
- Carpenter's rule problem (Robert Connelly, Erik Demaine, Günter Rote, 2003)
- Nagata's conjecture (Ivan Shestakov, Ualbai Umirbaev, 2003)
- Double bubble conjecture (Michael Hutchings, Frank Morgan, Manuel Ritoré, Antonio Ros, 2002)
20th century
- Honeycomb conjecture (Thomas Callister Hales, 1999)
- Bogomolov conjecture (Emmanuel Ullmo, 1998, Shou-Wu Zhang, 1998)
- Kepler conjecture (Samuel Ferguson, Thomas Callister Hales, 1998)
- Dodecahedral conjecture (Thomas Callister Hales, Sean McLaughlin, 1998)
Graph theory
- Blankenship–Oporowski conjecture on the book thickness of subdivisions (Vida Dujmović, David Eppstein, Robert Hickingbotham, Pat Morin, and David Wood, 2021)
- Ringel's conjecture on graceful labeling of trees (Richard Montgomery, Benny Sudakov, Alexey Pokrovskiy, 2020)
- Disproof of Hedetniemi's conjecture on the chromatic number of tensor products of graphs (Yaroslav Shitov, 2019)
- Babai's problem (Alireza Abdollahi, Maysam Zallaghi, 2015)
- Alspach's conjecture (Darryn Bryant, Daniel Horsley, William Pettersson, 2014)
- Scheinerman's conjecture (Jeremie Chalopin and Daniel Gonçalves, 2009)
- Erdős–Menger conjecture (Ron Aharoni, Eli Berger 2007)
- Road coloring conjecture (Avraham Trahtman, 2007)
- Robertson–Seymour theorem (Neil Robertson, Paul Seymour, 2004)
- Strong perfect graph conjecture (Maria Chudnovsky, Neil Robertson, Paul Seymour and Robin Thomas, 2002)
Group theory
- Hanna Neumann conjecture (Joel Friedman, 2011, Igor Mineyev, 2011)
- Density theorem (Hossein Namazi, Juan Souto, 2010)
- Full classification of finite simple groups (Koichiro Harada, Ronald Solomon, 2008)
Number theory
21st century
- Duffin-Schaeffer conjecture (Dimitris Koukoulopoulos, James Maynard, 2019)
- Main conjecture in Vinogradov's mean-value theorem (Jean Bourgain, Ciprian Demeter, Larry Guth, 2015)
- Goldbach's weak conjecture (Harald Helfgott, 2013)
- Existence of bounded gaps between primes (Yitang Zhang, Polymath8, James Maynard, 2013)
- Sidon set problem (Javier Cilleruelo, Imre Z. Ruzsa, and Carlos Vinuesa, 2010)
- Serre's modularity conjecture (Chandrashekhar Khare and Jean-Pierre Wintenberger, 2008)
- Green–Tao theorem (Ben J. Green and Terence Tao, 2004)
- Catalan's conjecture (Preda Mihăilescu, 2002)
- Erdős–Graham problem (Ernest S. Croot III, 2000)
20th century
- Lafforgue's theorem (Laurent Lafforgue, 1998)
- Fermat's Last Theorem (Andrew Wiles and Richard Taylor, 1995)
Ramsey theory
- Burr–Erdős conjecture (Choongbum Lee, 2017)
- Boolean Pythagorean triples problem (Marijn Heule, Oliver Kullmann, Victor W. Marek, 2016)
Theoretical computer science
- Sensitivity conjecture for Boolean functions (Hao Huang, 2019)
Topology
- Deciding whether the Conway knot is a slice knot (Lisa Piccirillo, 2020)
- Virtual Haken conjecture (Ian Agol, Daniel Groves, Jason Manning, 2012) (and by work of Daniel Wise also virtually fibered conjecture)
- Hsiang–Lawson's conjecture (Simon Brendle, 2012)
- Ehrenpreis conjecture (Jeremy Kahn, Vladimir Markovic, 2011)
- Atiyah conjecture (Austin, 2009)
- Cobordism hypothesis (Jacob Lurie, 2008)
- Spherical space form conjecture (Grigori Perelman, 2006)
- Poincaré conjecture (Grigori Perelman, 2002)
- Geometrization conjecture, proven by Grigori Perelman in a series of preprints in 2002–2003.
- Disproof of the Ganea conjecture (Iwase, 1997)
Uncategorised
21st century
2010s
- Erdős discrepancy problem (Terence Tao, 2015)
- Umbral moonshine conjecture (John F. R. Duncan, Michael J. Griffin, Ken Ono, 2015)
- Anderson conjecture on the finite number of diffeomorphism classes of the collection of 4-manifolds satisfying certain properties (Jeff Cheeger, Aaron Naber, 2014)
- Gaussian correlation inequality (Thomas Royen, 2014)
- Beck's conjecture on discrepancies of set systems constructed from three permutations (Alantha Newman, Aleksandar Nikolov, 2011)
- Bloch–Kato conjecture (Vladimir Voevodsky, 2011) (and Quillen–Lichtenbaum conjecture and by work of Thomas Geisser and Marc Levine (2001) also Beilinson–Lichtenbaum conjecture)
2000s
- Kauffman–Harary conjecture (Thomas Mattman, Pablo Solis, 2009)
- Surface subgroup conjecture (Jeremy Kahn, Vladimir Markovic, 2009)
- Normal scalar curvature conjecture and the Böttcher–Wenzel conjecture (Zhiqin Lu, 2007)
- Nirenberg–Treves conjecture (Nils Dencker, 2005)
- Lax conjecture (Adrian Lewis, Pablo Parrilo, Motakuri Ramana, 2005)
- The Langlands–Shelstad fundamental lemma (Ngô Bảo Châu and Gérard Laumon, 2004)
- Milnor conjecture (Vladimir Voevodsky, 2003)
- Kirillov's conjecture (Ehud Baruch, 2003)
- Kouchnirenko’s conjecture (Bertrand Haas, 2002)
- n! conjecture (Mark Haiman, 2001) (and also Macdonald positivity conjecture)
- Kato's conjecture (Pascal Auscher, Steve Hofmann, Michael Lacey, Alan McIntosh, and Philipp Tchamitchian, 2001)
- Deligne's conjecture on 1-motives (Luca Barbieri-Viale, Andreas Rosenschon, Morihiko Saito, 2001)
- Modularity theorem (Christophe Breuil, Brian Conrad, Fred Diamond, and Richard Taylor, 2001)
- Erdős–Stewart conjecture (Florian Luca, 2001)
- Berry–Robbins problem (Michael Atiyah, 2000)
20th century
- Torsion conjecture (Loïc Merel, 1996)
- Harary's conjecture on the integral sum number of complete graphs (Zhibo Chen, 1996)
See also
- List of conjectures
- List of unsolved problems in statistics
- List of unsolved problems in computer science
- List of unsolved problems in physics
- Lists of unsolved problems
- Open Problems in Mathematics
- The Great Mathematical Problems
- Scottish Book
References
- Thiele, Rüdiger (2005), "On Hilbert and his twenty-four problems", in Van Brummelen, Glen (ed.), Mathematics and the historian's craft. The Kenneth O. May Lectures, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, vol. 21, pp. 243–295, ISBN 978-0-387-25284-1
- Guy, Richard (1994), Unsolved Problems in Number Theory (2nd ed.), Springer, p. vii, ISBN 978-1-4899-3585-4, archived from the original on 2019-03-23, retrieved 2016-09-22.
- Shimura, G. (1989). "Yutaka Taniyama and his time". Bulletin of the London Mathematical Society. 21 (2): 186–196. doi:10.1112/blms/21.2.186.
- Friedl, Stefan (2014). "Thurston's vision and the virtual fibering theorem for 3-manifolds". Jahresbericht der Deutschen Mathematiker-Vereinigung. 116 (4): 223–241. doi:10.1365/s13291-014-0102-x. MR 3280572. S2CID 56322745.
- Thurston, William P. (1982). "Three-dimensional manifolds, Kleinian groups and hyperbolic geometry". Bulletin of the American Mathematical Society. New Series. 6 (3): 357–381. doi:10.1090/S0273-0979-1982-15003-0. MR 0648524.
- ^ "Millennium Problems". claymath.org. Archived from the original on 2017-06-06. Retrieved 2015-01-20.
- "Fields Medal awarded to Artur Avila". Centre national de la recherche scientifique. 2014-08-13. Archived from the original on 2018-07-10. Retrieved 2018-07-07.
- Bellos, Alex (2014-08-13). "Fields Medals 2014: the maths of Avila, Bhargava, Hairer and Mirzakhani explained". The Guardian. Archived from the original on 2016-10-21. Retrieved 2018-07-07.
- Abe, Jair Minoro; Tanaka, Shotaro (2001). Unsolved Problems on Mathematics for the 21st Century. IOS Press. ISBN 978-9051994902.
- "DARPA invests in math". CNN. 2008-10-14. Archived from the original on 2009-03-04. Retrieved 2013-01-14.
- "Broad Agency Announcement (BAA 07-68) for Defense Sciences Office (DSO)". DARPA. 2007-09-10. Archived from the original on 2012-10-01. Retrieved 2013-06-25.
- "Poincaré Conjecture". Clay Mathematics Institute. Archived from the original on 2013-12-15.
- "Smooth 4-dimensional Poincare conjecture". Open Problem Garden. Archived from the original on 2018-01-25. Retrieved 2019-08-06.
- Dowling, T. A. (February 1973). "A class of geometric lattices based on finite groups". Journal of Combinatorial Theory. Series B. 14 (1): 61–86. doi:10.1016/S0095-8956(73)80007-3.
- * ДНЕСТРОВСКАЯ ТЕТРАДЪ [DNIESTER NOTEBOOK] (PDF) (in Russian), The Russian Academy of Sciences, 1993
- "Dniester Notebook: Unsolved Problems in the Theory of Rings and Modules" (PDF), University of Saskatchewan, retrieved 2019-08-15
- Эрлаголъская тетрадъ [Erlagol notebook] (PDF) (in Russian), The Novosibirsk State University, 2018
- ^ Waldschmidt, Michel (2013), Diophantine Approximation on Linear Algebraic Groups: Transcendence Properties of the Exponential Function in Several Variables, Springer, pp. 14, 16, ISBN 9783662115695
- Kung, H. T.; Traub, Joseph Frederick (1974), "Optimal order of one-point and multipoint iteration", Journal of the ACM, 21 (4): 643–651, doi:10.1145/321850.321860, S2CID 74921
- Smyth, Chris (2008), "The Mahler measure of algebraic numbers: a survey", in McKee, James; Smyth, Chris (eds.), Number Theory and Polynomials, London Mathematical Society Lecture Note Series, vol. 352, Cambridge University Press, pp. 322–349, ISBN 978-0-521-71467-9
- Berenstein, Carlos A. (2001) , "Pompeiu problem", Encyclopedia of Mathematics, EMS Press
- For some background on the numbers in this problem, see articles by Eric W. Weisstein at Wolfram MathWorld (all articles accessed 15 December 2014):
- pi (Archived 2014-12-06 at the Wayback Machine)
- e (Archived 2014-11-21 at the Wayback Machine)
- Khinchin's Constant (Archived 2014-11-05 at the Wayback Machine)
- irrational numbers (Archived 2015-03-27 at the Wayback Machine)
- transcendental numbers (Archived 2014-11-13 at the Wayback Machine)
- irrationality measures (Archived 2015-04-21 at the Wayback Machine)
- Waldschmidt, Michel (2008). An introduction to irrationality and transcendence methods (PDF). 2008 Arizona Winter School. Archived from the original (PDF) on 16 December 2014. Retrieved 15 December 2014.
- Albert, John, Some unsolved problems in number theory (PDF), archived from the original (PDF) on 17 December 2014, retrieved 15 December 2014
{{citation}}:|archive-date=/|archive-url=timestamp mismatch; 17 January 2014 suggested (help) - Brightwell, Graham R.; Felsner, Stefan; Trotter, William T. (1995), "Balancing pairs and the cross product conjecture", Order, 12 (4): 327–349, CiteSeerX 10.1.1.38.7841, doi:10.1007/BF01110378, MR 1368815, S2CID 14793475.
- Tao, Terence (2018). "Some remarks on the lonely runner conjecture". Contributions to Discrete Mathematics. 13 (2): 1–31. arXiv:1701.02048. doi:10.11575/cdm.v13i2.62728.
- Bruhn, Henning; Schaudt, Oliver (2015), "The journey of the union-closed sets conjecture" (PDF), Graphs and Combinatorics, 31 (6): 2043–2074, arXiv:1309.3297, doi:10.1007/s00373-014-1515-0, MR 3417215, S2CID 17531822, archived (PDF) from the original on 2017-08-08, retrieved 2017-07-18
- "Dedekind Numbers and Related Sequences" (PDF). Archived from the original (PDF) on 2015-03-15. Retrieved 2020-04-30.
- Murnaghan, F. D. (1938), "The Analysis of the Direct Product of Irreducible Representations of the Symmetric Groups", American Journal of Mathematics, 60 (1): 44–65, doi:10.2307/2371542, JSTOR 2371542, MR 1507301, PMC 1076971, PMID 16577800
- Liśkiewicz, Maciej; Ogihara, Mitsunori; Toda, Seinosuke (2003-07-28). "The complexity of counting self-avoiding walks in subgraphs of two-dimensional grids and hypercubes". Theoretical Computer Science. 304 (1): 129–156. doi:10.1016/S0304-3975(03)00080-X.
- S. M. Ulam, Problems in Modern Mathematics. Science Editions John Wiley & Sons, Inc., New York, 1964, page 76.
- Kaloshin, Vadim; Sorrentino, Alfonso (2018). "On the local Birkhoff conjecture for convex billiards". Annals of Mathematics. 188 (1): 315–380. arXiv:1612.09194. doi:10.4007/annals.2018.188.1.6. S2CID 119171182.
- Sarnak, Peter (2011), "Recent progress on the quantum unique ergodicity conjecture", Bulletin of the American Mathematical Society, 48 (2): 211–228, doi:10.1090/S0273-0979-2011-01323-4, MR 2774090
- Paul Halmos, Ergodic theory. Chelsea, New York, 1956.
- Kari, Jarkko (2009). "Structure of reversible cellular automata". Structure of Reversible Cellular Automata. International Conference on Unconventional Computation. Lecture Notes in Computer Science. Vol. 5715. Springer. p. 6. Bibcode:2009LNCS.5715....6K. doi:10.1007/978-3-642-03745-0_5. ISBN 978-3-642-03744-3.
- ^ http://english.log-it-ex.com Archived 2017-11-10 at the Wayback Machine Ten open questions about Sudoku (2012-01-21).
- "Higher-Dimensional Tic-Tac-Toe". PBS Infinite Series. YouTube. 2017-09-21. Archived from the original on 2017-10-11. Retrieved 2018-07-29.
- Barlet, Daniel; Peternell, Thomas; Schneider, Michael (1990). "On two conjectures of Hartshorne's". Mathematische Annalen. 286 (1–3): 13–25. doi:10.1007/BF01453563. S2CID 122151259.
- Maulik, Davesh; Nekrasov, Nikita; Okounov, Andrei; Pandharipande, Rahul (2004-06-05), Gromov–Witten theory and Donaldson–Thomas theory, I, arXiv:math/0312059, Bibcode:2003math.....12059M
- Zariski, Oscar (1971). "Some open questions in the theory of singularities". Bulletin of the American Mathematical Society. 77 (4): 481–491. doi:10.1090/S0002-9904-1971-12729-5. MR 0277533.
- Bereg, Sergey; Dumitrescu, Adrian; Jiang, Minghui (2010), "On covering problems of Rado", Algorithmica, 57 (3): 538–561, doi:10.1007/s00453-009-9298-z, MR 2609053, S2CID 6511998
- Melissen, Hans (1993), "Densest packings of congruent circles in an equilateral triangle", American Mathematical Monthly, 100 (10): 916–925, doi:10.2307/2324212, JSTOR 2324212, MR 1252928
- Conway, John H.; Neil J.A. Sloane (1999), Sphere Packings, Lattices and Groups (3rd ed.), New York: Springer-Verlag, pp. 21–22, ISBN 978-0-387-98585-5
- Hales, Thomas (2017), The Reinhardt conjecture as an optimal control problem, arXiv:1703.01352
- Brass, Peter; Moser, William; Pach, János (2005), Research Problems in Discrete Geometry, New York: Springer, p. 45, ISBN 978-0387-23815-9, MR 2163782
- Gardner, Martin (1995), New Mathematical Diversions (Revised Edition), Washington: Mathematical Association of America, p. 251
- Barros, Manuel (1997), "General Helices and a Theorem of Lancret", Proceedings of the American Mathematical Society, 125 (5): 1503–1509, doi:10.1090/S0002-9939-97-03692-7, JSTOR 2162098
- Katz, Mikhail G. (2007), Systolic geometry and topology, Mathematical Surveys and Monographs, vol. 137, American Mathematical Society, Providence, RI, p. 57, doi:10.1090/surv/137, ISBN 978-0-8218-4177-8, MR 2292367
- Rosenberg, Steven (1997), The Laplacian on a Riemannian Manifold: An introduction to analysis on manifolds, London Mathematical Society Student Texts, vol. 31, Cambridge: Cambridge University Press, pp. 62–63, doi:10.1017/CBO9780511623783, ISBN 978-0-521-46300-3, MR 1462892
- Boltjansky, V.; Gohberg, I. (1985), "11. Hadwiger's Conjecture", Results and Problems in Combinatorial Geometry, Cambridge University Press, pp. 44–46.
- Morris, Walter D.; Soltan, Valeriu (2000), "The Erdős-Szekeres problem on points in convex position—a survey", Bull. Amer. Math. Soc., 37 (4): 437–458, doi:10.1090/S0273-0979-00-00877-6, MR 1779413; Suk, Andrew (2016), "On the Erdős–Szekeres convex polygon problem", J. Amer. Math. Soc., 30 (4): 1047–1053, arXiv:1604.08657, doi:10.1090/jams/869, S2CID 15732134
- Kalai, Gil (1989), "The number of faces of centrally-symmetric polytopes", Graphs and Combinatorics, 5 (1): 389–391, doi:10.1007/BF01788696, MR 1554357, S2CID 8917264.
- Weisstein, Eric W. "Kobon Triangle". MathWorld.
- Guy, Richard K. (1983), "An olla-podrida of open problems, often oddly posed", American Mathematical Monthly, 90 (3): 196–200, doi:10.2307/2975549, JSTOR 2975549, MR 1540158
- Matoušek, Jiří (2002), Lectures on discrete geometry, Graduate Texts in Mathematics, vol. 212, Springer-Verlag, New York, p. 206, doi:10.1007/978-1-4613-0039-7, ISBN 978-0-387-95373-1, MR 1899299
- Brass, Peter; Moser, William; Pach, János (2005), "5.1 The Maximum Number of Unit Distances in the Plane", Research problems in discrete geometry, Springer, New York, pp. 183–190, ISBN 978-0-387-23815-9, MR 2163782
- Dey, Tamal K. (1998), "Improved bounds for planar k-sets and related problems", Discrete Comput. Geom., 19 (3): 373–382, doi:10.1007/PL00009354, MR 1608878; Tóth, Gábor (2001), "Point sets with many k-sets", Discrete Comput. Geom., 26 (2): 187–194, doi:10.1007/s004540010022, MR 1843435.
- Aronov, Boris; Dujmović, Vida; Morin, Pat; Ooms, Aurélien; Schultz Xavier da Silveira, Luís Fernando (2019), "More Turán-type theorems for triangles in convex point sets", Electronic Journal of Combinatorics, 26 (1): P1.8, arXiv:1706.10193, Bibcode:2017arXiv170610193A, doi:10.37236/7224, archived from the original on 2019-02-18, retrieved 2019-02-18
- Atiyah, Michael (2001), "Configurations of points", Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 359 (1784): 1375–1387, Bibcode:2001RSPTA.359.1375A, doi:10.1098/rsta.2001.0840, ISSN 1364-503X, MR 1853626, S2CID 55833332
- Finch, S. R.; Wetzel, J. E. (2004), "Lost in a forest", American Mathematical Monthly, 11 (8): 645–654, doi:10.2307/4145038, JSTOR 4145038, MR 2091541
- Solomon, Yaar; Weiss, Barak (2016), "Dense forests and Danzer sets", Annales Scientifiques de l'École Normale Supérieure, 49 (5): 1053–1074, arXiv:1406.3807, doi:10.24033/asens.2303, MR 3581810, S2CID 672315; Conway, John H., Five $1,000 Problems (Update 2017) (PDF), On-Line Encyclopedia of Integer Sequences, archived (PDF) from the original on 2019-02-13, retrieved 2019-02-12
- Socolar, Joshua E. S.; Taylor, Joan M. (2012), "Forcing nonperiodicity with a single tile", The Mathematical Intelligencer, 34 (1): 18–28, arXiv:1009.1419, doi:10.1007/s00283-011-9255-y, MR 2902144, S2CID 10747746
- Arutyunyants, G.; Iosevich, A. (2004), "Falconer conjecture, spherical averages and discrete analogs", in Pach, János (ed.), Towards a Theory of Geometric Graphs, Contemp. Math., vol. 342, Amer. Math. Soc., Providence, RI, pp. 15–24, doi:10.1090/conm/342/06127, ISBN 9780821834848, MR 2065249
- Matschke, Benjamin (2014), "A survey on the square peg problem", Notices of the American Mathematical Society, 61 (4): 346–352, doi:10.1090/noti1100
- Katz, Nets; Tao, Terence (2002), "Recent progress on the Kakeya conjecture", Proceedings of the 6th International Conference on Harmonic Analysis and Partial Differential Equations (El Escorial, 2000), Publicacions Matemàtiques (Vol. Extra): 161–179, CiteSeerX 10.1.1.241.5335, doi:10.5565/PUBLMAT_Esco02_07, MR 1964819, S2CID 77088
{{citation}}:|issue=has extra text (help) - Weaire, Denis, ed. (1997), The Kelvin Problem, CRC Press, p. 1, ISBN 9780748406326
- Brass, Peter; Moser, William; Pach, János (2005), Research problems in discrete geometry, New York: Springer, p. 457, ISBN 9780387299297, MR 2163782
- Mahler, Kurt (1939). "Ein Minimalproblem für konvexe Polygone". Mathematica (Zutphen) B: 118–127.
- Norwood, Rick; Poole, George; Laidacker, Michael (1992), "The worm problem of Leo Moser", Discrete and Computational Geometry, 7 (2): 153–162, doi:10.1007/BF02187832, MR 1139077
- Wagner, Neal R. (1976), "The Sofa Problem" (PDF), The American Mathematical Monthly, 83 (3): 188–189, doi:10.2307/2977022, JSTOR 2977022, archived (PDF) from the original on 2015-04-20, retrieved 2014-05-14
- Chai, Ying; Yuan, Liping; Zamfirescu, Tudor (June–July 2018), "Rupert Property of Archimedean Solids", The American Mathematical Monthly, 125 (6): 497–504, doi:10.1080/00029890.2018.1449505, S2CID 125508192
- Steininger, Jakob; Yurkevich, Sergey (December 27, 2021), An algorithmic approach to Rupert's problem, arXiv:2112.13754
- Demaine, Erik D.; O'Rourke, Joseph (2007), "Chapter 22. Edge Unfolding of Polyhedra", Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Cambridge University Press, pp. 306–338
- Ghomi, Mohammad (2018-01-01). "D "urer's Unfolding Problem for Convex Polyhedra". Notices of the American Mathematical Society. 65 (1): 25–27. doi:10.1090/noti1609. ISSN 0002-9920.
- Whyte, L. L. (1952), "Unique arrangements of points on a sphere", The American Mathematical Monthly, 59 (9): 606–611, doi:10.2307/2306764, JSTOR 2306764, MR 0050303
- Howards, Hugh Nelson (2013), "Forming the Borromean rings out of arbitrary polygonal unknots", Journal of Knot Theory and Its Ramifications, 22 (14): 1350083, 15, arXiv:1406.3370, doi:10.1142/S0218216513500831, MR 3190121, S2CID 119674622
- Brandts, Jan; Korotov, Sergey; Křížek, Michal; Šolc, Jakub (2009), "On nonobtuse simplicial partitions" (PDF), SIAM Review, 51 (2): 317–335, Bibcode:2009SIAMR..51..317B, doi:10.1137/060669073, MR 2505583, archived (PDF) from the original on 2018-11-04, retrieved 2018-11-22. See in particular Conjecture 23, p. 327.
- ACW (May 24, 2012), "Convex uniform 5-polytopes", Open Problem Garden, archived from the original on October 5, 2016, retrieved 2016-10-04.
- Bousquet, Nicolas; Bartier, Valentin (2019), "Linear Transformations Between Colorings in Chordal Graphs", in Bender, Michael A.; Svensson, Ola; Herman, Grzegorz (eds.), 27th Annual European Symposium on Algorithms, ESA 2019, September 9-11, 2019, Munich/Garching, Germany, LIPIcs, vol. 144, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, pp. 24:1–24:15, doi:10.4230/LIPIcs.ESA.2019.24, ISBN 9783959771245, S2CID 195791634
{{citation}}: CS1 maint: unflagged free DOI (link) - Chung, Fan; Graham, Ron (1998), Erdős on Graphs: His Legacy of Unsolved Problems, A K Peters, pp. 97–99.
- Chudnovsky, Maria; Seymour, Paul (2014), "Extending the Gyárfás-Sumner conjecture", Journal of Combinatorial Theory, Series B, 105: 11–16, doi:10.1016/j.jctb.2013.11.002, MR 3171779
- Toft, Bjarne (1996), "A survey of Hadwiger's conjecture", Congressus Numerantium, 115: 249–283, MR 1411244.
- Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991), Unsolved Problems in Geometry, Springer-Verlag, Problem G10.
- Hägglund, Jonas; Steffen, Eckhard (2014), "Petersen-colorings and some families of snarks", Ars Mathematica Contemporanea, 7 (1): 161–173, doi:10.26493/1855-3974.288.11a, MR 3047618, archived from the original on 2016-10-03, retrieved 2016-09-30.
- Jensen, Tommy R.; Toft, Bjarne (1995), "12.20 List-Edge-Chromatic Numbers", Graph Coloring Problems, New York: Wiley-Interscience, pp. 201–202, ISBN 978-0-471-02865-9.
- Molloy, Michael; Reed, Bruce (1998), "A bound on the total chromatic number", Combinatorica, 18 (2): 241–280, CiteSeerX 10.1.1.24.6514, doi:10.1007/PL00009820, MR 1656544, S2CID 9600550.
- Barát, János; Tóth, Géza (2010), "Towards the Albertson Conjecture", Electronic Journal of Combinatorics, 17 (1): R73, arXiv:0909.0413, Bibcode:2009arXiv0909.0413B, doi:10.37236/345.
- Fulek, Radoslav; Pach, János (2011), "A computational approach to Conway's thrackle conjecture", Computational Geometry, 44 (6–7): 345–355, arXiv:1002.3904, doi:10.1016/j.comgeo.2011.02.001, MR 2785903.
- Hartsfield, Nora; Ringel, Gerhard (2013), Pearls in Graph Theory: A Comprehensive Introduction, Dover Books on Mathematics, Courier Dover Publications, p. 247, ISBN 978-0-486-31552-2, MR 2047103.
- Hliněný, Petr (2010), "20 years of Negami's planar cover conjecture" (PDF), Graphs and Combinatorics, 26 (4): 525–536, CiteSeerX 10.1.1.605.4932, doi:10.1007/s00373-010-0934-9, MR 2669457, S2CID 121645, archived (PDF) from the original on 2016-03-04, retrieved 2016-10-04.
- Nöllenburg, Martin; Prutkin, Roman; Rutter, Ignaz (2016), "On self-approaching and increasing-chord drawings of 3-connected planar graphs", Journal of Computational Geometry, 7 (1): 47–69, arXiv:1409.0315, doi:10.20382/jocg.v7i1a3, MR 3463906, S2CID 1500695
- Pach, János; Sharir, Micha (2009), "5.1 Crossings—the Brick Factory Problem", Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical Surveys and Monographs, vol. 152, American Mathematical Society, pp. 126–127.
- Demaine, E.; O'Rourke, J. (2002–2012), "Problem 45: Smallest Universal Set of Points for Planar Graphs", The Open Problems Project, archived from the original on 2012-08-14, retrieved 2013-03-19.
- Florek, Jan (2010), "On Barnette's conjecture", Discrete Mathematics, 310 (10–11): 1531–1535, doi:10.1016/j.disc.2010.01.018, MR 2601261.
- Broersma, Hajo; Patel, Viresh; Pyatkin, Artem (2014), "On toughness and Hamiltonicity of $2K_2$-free graphs", Journal of Graph Theory, 75 (3): 244–255, doi:10.1002/jgt.21734, MR 3153119, S2CID 1377980
- Jaeger, F. (1985), "A survey of the cycle double cover conjecture", Annals of Discrete Mathematics 27 – Cycles in Graphs, North-Holland Mathematics Studies, vol. 27, pp. 1–12, doi:10.1016/S0304-0208(08)72993-1, ISBN 9780444878038.
- Heckman, Christopher Carl; Krakovski, Roi (2013), "Erdös-Gyárfás conjecture for cubic planar graphs", Electronic Journal of Combinatorics, 20 (2), P7, doi:10.37236/3252.
- Akiyama, Jin; Exoo, Geoffrey; Harary, Frank (1981), "Covering and packing in graphs. IV. Linear arboricity", Networks, 11 (1): 69–72, doi:10.1002/net.3230110108, MR 0608921.
- L. Babai, Automorphism groups, isomorphism, reconstruction Archived 2007-06-13 at the Wayback Machine, in Handbook of Combinatorics, Vol. 2, Elsevier, 1996, 1447–1540.
- Lenz, Hanfried; Ringel, Gerhard (1991), "A brief review on Egmont Köhler's mathematical work", Discrete Mathematics, 97 (1–3): 3–16, doi:10.1016/0012-365X(91)90416-Y, MR 1140782
- ^ Words and Graphs. Monographs in Theoretical Computer Science. An EATCS Series. 2015. doi:10.1007/978-3-319-25859-1. ISBN 978-3-319-25857-7. S2CID 7727433 – via link.springer.com.
- ^ Kitaev, Sergey (2017-05-16). A Comprehensive Introduction to the Theory of Word-Representable Graphs. International Conference on Developments in Language Theory. doi:10.1007/978-3-319-62809-7_2.
- ^ Kitaev, S. V.; Pyatkin, A. V. (April 1, 2018). "Word-Representable Graphs: a Survey". Journal of Applied and Industrial Mathematics. 12 (2): 278–296. doi:10.1134/S1990478918020084. S2CID 125814097 – via Springer Link.
- ^ Kitaev, Sergey V.; Pyatkin, Artem V. (2018). "Графы, представимые в виде слов. Обзор результатов" [Word-representable graphs: A survey]. Дискретн. анализ и исслед. опер. (in Russian). 25 (2): 19–53. doi:10.17377/daio.2018.25.588.
- Marc Elliot Glen (2016). "Colourability and word-representability of near-triangulations". arXiv:1605.01688 .
- Kitaev, Sergey (2014-03-06). "On graphs with representation number 3". doi:10.48550/arXiv.1403.1616.
{{cite journal}}: Cite journal requires|journal=(help) - Glen, Marc; Kitaev, Sergey; Pyatkin, Artem (2018). "On the representation number of a crown graph". Discrete Applied Mathematics. 244: 89–93. arXiv:1609.00674. doi:10.1016/j.dam.2018.03.013. S2CID 46925617.
- Conway, John H., Five $1,000 Problems (Update 2017) (PDF), Online Encyclopedia of Integer Sequences, archived (PDF) from the original on 2019-02-13, retrieved 2019-02-12
- Chudnovsky, Maria (2014), "The Erdös–Hajnal conjecture—a survey" (PDF), Journal of Graph Theory, 75 (2): 178–190, arXiv:1606.08827, doi:10.1002/jgt.21730, MR 3150572, S2CID 985458, Zbl 1280.05086, archived (PDF) from the original on 2016-03-04, retrieved 2016-09-22.
- Gupta, Anupam; Newman, Ilan; Rabinovich, Yuri; Sinclair, Alistair (2004), "Cuts, trees and -embeddings of graphs", Combinatorica, 24 (2): 233–269, CiteSeerX 10.1.1.698.8978, doi:10.1007/s00493-004-0015-x, MR 2071334, S2CID 46133408
- Pleanmani, Nopparat (2019), "Graham's pebbling conjecture holds for the product of a graph and a sufficiently large complete bipartite graph", Discrete Mathematics, Algorithms and Applications, 11 (6): 1950068, 7, doi:10.1142/s179383091950068x, MR 4044549, S2CID 204207428
- Spinrad, Jeremy P. (2003), "2. Implicit graph representation", Efficient Graph Representations, pp. 17–30, ISBN 978-0-8218-2815-1.
- "Jorgensen's Conjecture", Open Problem Garden, archived from the original on 2016-11-14, retrieved 2016-11-13.
- Baird, William; Bonato, Anthony (2012), "Meyniel's conjecture on the cop number: a survey", Journal of Combinatorics, 3 (2): 225–238, arXiv:1308.3385, doi:10.4310/JOC.2012.v3.n2.a6, MR 2980752, S2CID 18942362
- Schwenk, Allen (2012), "Some History on the Reconstruction Conjecture" (PDF), Joint Mathematics Meetings, archived (PDF) from the original on 2015-04-09, retrieved 2018-11-26
- Ramachandran, S. (1981), "On a new digraph reconstruction conjecture", Journal of Combinatorial Theory, Series B, 31 (2): 143–149, doi:10.1016/S0095-8956(81)80019-6, MR 0630977
- Seymour's 2nd Neighborhood Conjecture Archived 2019-01-11 at the Wayback Machine, Open Problems in Graph Theory and Combinatorics, Douglas B. West.
- Blokhuis, A.; Brouwer, A. E. (1988), "Geodetic graphs of diameter two", Geometriae Dedicata, 25 (1–3): 527–533, doi:10.1007/BF00191941, MR 0925851, S2CID 189890651
- Kühn, Daniela; Mycroft, Richard; Osthus, Deryk (2011), "A proof of Sumner's universal tournament conjecture for large tournaments", Proceedings of the London Mathematical Society, Third Series, 102 (4): 731–766, arXiv:1010.4430, doi:10.1112/plms/pdq035, MR 2793448, S2CID 119169562, Zbl 1218.05034.
- 4-flow conjecture Archived 2018-11-26 at the Wayback Machine and 5-flow conjecture Archived 2018-11-26 at the Wayback Machine, Open Problem Garden
- Brešar, Boštjan; Dorbec, Paul; Goddard, Wayne; Hartnell, Bert L.; Henning, Michael A.; Klavžar, Sandi; Rall, Douglas F. (2012), "Vizing's conjecture: a survey and recent results", Journal of Graph Theory, 69 (1): 46–76, CiteSeerX 10.1.1.159.7029, doi:10.1002/jgt.20565, MR 2864622, S2CID 9120720.
- Ducey, Joshua E. (2017), "On the critical group of the missing Moore graph", Discrete Mathematics, 340 (5): 1104–1109, arXiv:1509.00327, doi:10.1016/j.disc.2016.10.001, MR 3612450, S2CID 28297244
- Fomin, Fedor V.; Høie, Kjartan (2006), "Pathwidth of cubic graphs and exact algorithms", Information Processing Letters, 97 (5): 191–196, doi:10.1016/j.ipl.2005.10.012, MR 2195217
- Aschbacher, Michael (1990), "On Conjectures of Guralnick and Thompson", Journal of Algebra, 135 (2): 277–343, doi:10.1016/0021-8693(90)90292-V
- Khukhro, Evgeny I.; Mazurov, Victor D. (2019), Unsolved Problems in Group Theory. The Kourovka Notebook, arXiv:1401.0300v16
- Hrushovski, Ehud (1989). "Kueker's conjecture for stable theories". Journal of Symbolic Logic. 54 (1): 207–220. doi:10.2307/2275025. JSTOR 2275025. S2CID 41940041.
- ^ Shelah S, Classification Theory, North-Holland, 1990
- Shelah, Saharon (2009). Classification theory for abstract elementary classes. College Publications. ISBN 978-1-904987-71-0.
- Peretz, Assaf (2006). "Geometry of forking in simple theories". Journal of Symbolic Logic. 71 (1): 347–359. arXiv:math/0412356. doi:10.2178/jsl/1140641179. S2CID 9380215.
- Cherlin, G.; Shelah, S. (May 2007). "Universal graphs with a forbidden subtree". Journal of Combinatorial Theory, Series B. 97 (3): 293–333. arXiv:math/0512218. doi:10.1016/j.jctb.2006.05.008. S2CID 10425739.
- Džamonja, Mirna, "Club guessing and the universal models." On PCF, ed. M. Foreman, (Banff, Alberta, 2004).
- Shelah, Saharon (1999). "Borel sets with large squares". Fundamenta Mathematicae. 159 (1): 1–50. arXiv:math/9802134. Bibcode:1998math......2134S. doi:10.4064/fm-159-1-1-50. S2CID 8846429.
- Baldwin, John T. (July 24, 2009). Categoricity (PDF). American Mathematical Society. ISBN 978-0-8218-4893-7. Archived (PDF) from the original on July 29, 2010. Retrieved February 20, 2014.
- Shelah, Saharon (2009). "Introduction to classification theory for abstract elementary classes". arXiv:0903.3428. Bibcode:2009arXiv0903.3428S.
{{cite journal}}: Cite journal requires|journal=(help) - Gurevich, Yuri, "Monadic Second-Order Theories," in J. Barwise, S. Feferman, eds., Model-Theoretic Logics (New York: Springer-Verlag, 1985), 479–506.
- Makowsky J, "Compactness, embeddings and definability," in Model-Theoretic Logics, eds Barwise and Feferman, Springer 1985 pps. 645–715.
- Keisler, HJ (1967). "Ultraproducts which are not saturated". J. Symb. Log. 32 (1): 23–46. doi:10.2307/2271240. JSTOR 2271240. S2CID 250345806.
- Malliaris M, Shelah S, "A dividing line in simple unstable theories." https://arxiv.org/abs/1208.2140 Archived 2017-08-02 at the Wayback Machine
- Conrey, Brian (2016), "Lectures on the Riemann zeta function (book review)", Bulletin of the American Mathematical Society, 53 (3): 507–512, doi:10.1090/bull/1525
- Singmaster, D. (1971), "Research Problems: How often does an integer occur as a binomial coefficient?", American Mathematical Monthly, 78 (4): 385–386, doi:10.2307/2316907, JSTOR 2316907, MR 1536288.
- Aigner, Martin (2013), Markov's theorem and 100 years of the uniqueness conjecture, Cham: Springer, doi:10.1007/978-3-319-00888-2, ISBN 978-3-319-00887-5, MR 3098784
- Guo, Song; Sun, Zhi-Wei (2005), "On odd covering systems with distinct moduli", Advances in Applied Mathematics, 35 (2): 182–187, arXiv:math/0412217, doi:10.1016/j.aam.2005.01.004, MR 2152886, S2CID 835158
- "Are the Digits of Pi Random? Berkeley Lab Researcher May Hold Key". Archived from the original on 2016-03-27. Retrieved 2016-03-18.
- Robertson, John P. (1996-10-01). "Magic Squares of Squares". Mathematics Magazine. 69 (4): 289–293. doi:10.1080/0025570X.1996.11996457. ISSN 0025-570X.
- Huisman, Sander G. (2016). "Newer sums of three cubes". arXiv:1604.07746 .
- Dobson, J. B. (1 April 2017), "On Lerch's formula for the Fermat quotient", p. 23, arXiv:1103.3907v6
- Ribenboim, P. (2006). Die Welt der Primzahlen. Springer-Lehrbuch (in German) (2nd ed.). Springer. pp. 242–243. doi:10.1007/978-3-642-18079-8. ISBN 978-3-642-18078-1.
- Mazur, Barry (1992), "The topology of rational points", Experimental Mathematics, 1 (1): 35–45, doi:10.1080/10586458.1992.10504244, S2CID 17372107, archived from the original on 2019-04-07, retrieved 2019-04-07
- Kuperberg, Greg (1994), "Quadrisecants of knots and links", Journal of Knot Theory and Its Ramifications, 3: 41–50, arXiv:math/9712205, doi:10.1142/S021821659400006X, MR 1265452, S2CID 6103528
- Casazza, Peter G.; Fickus, Matthew; Tremain, Janet C.; Weber, Eric (2006). "The Kadison-Singer problem in mathematics and engineering: A detailed account". In Han, Deguang; Jorgensen, Palle E. T.; Larson, David Royal (eds.). Large Deviations for Additive Functionals of Markov Chains: The 25th Great Plains Operator Theory Symposium, June 7–12, 2005, University of Central Florida, Florida. Contemporary Mathematics. Vol. 414. American Mathematical Society. pp. 299–355. doi:10.1090/conm/414/07820. ISBN 978-0-8218-3923-2. Retrieved 24 April 2015.
- Mackenzie, Dana. "Kadison–Singer Problem Solved" (PDF). SIAM News. No. January/February 2014. Society for Industrial and Applied Mathematics. Archived (PDF) from the original on 23 October 2014. Retrieved 24 April 2015.
- ^ Agol, Ian (2004). "Tameness of hyperbolic 3-manifolds". arXiv:math/0405568.
- Kurdyka, Krzysztof; Mostowski, Tadeusz; Parusiński, Adam (2000). "Proof of the gradient conjecture of R. Thom". Annals of Mathematics. 152 (3): 763–792. arXiv:math/9906212. doi:10.2307/2661354. JSTOR 2661354. S2CID 119137528.
- Moreira, Joel; Richter, Florian K.; Robertson, Donald (2019). "A proof of a sumset conjecture of Erdős". Annals of Mathematics. 189 (2): 605–652. arXiv:1803.00498. doi:10.4007/annals.2019.189.2.4. S2CID 119158401.
- Stanley, Richard P. (1994), "A survey of Eulerian posets", in Bisztriczky, T.; McMullen, P.; Schneider, R.; Weiss, A. Ivić (eds.), Polytopes: abstract, convex and computational (Scarborough, ON, 1993), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 440, Dordrecht: Kluwer Academic Publishers, pp. 301–333, MR 1322068. See in particular p. 316.
- Kalai, Gil (2018-12-25). "Amazing: Karim Adiprasito proved the g-conjecture for spheres!". Archived from the original on 2019-02-16. Retrieved 2019-02-15.
- Santos, Franciscos (2012). "A counterexample to the Hirsch conjecture". Annals of Mathematics. 176 (1): 383–412. arXiv:1006.2814. doi:10.4007/annals.2012.176.1.7. S2CID 15325169.
- Ziegler, Günter M. (2012). "Who solved the Hirsch conjecture?". Documenta Mathematica. Extra Volume "Optimization Stories": 75–85.
- Chung, Fan; Greene, Curtis; Hutchinson, Joan (April 2015). "Herbert S. Wilf (1931–2012)". Notices of the AMS. 62 (4): 358. doi:10.1090/noti1247. ISSN 1088-9477. OCLC 34550461.
The conjecture was finally given an exceptionally elegant proof by A. Marcus and G. Tardos in 2004.
- Savchev, Svetoslav (2005). "Kemnitz' conjecture revisited". Discrete Mathematics. 297 (1–3): 196–201. doi:10.1016/j.disc.2005.02.018.
- Green, Ben (2004). "The Cameron–Erdős conjecture". The Bulletin of the London Mathematical Society. 36 (6): 769–778. arXiv:math.NT/0304058. doi:10.1112/S0024609304003650. MR 2083752. S2CID 119615076.
- "News from 2007". American Mathematical Society. AMS. 31 December 2007. Archived from the original on 17 November 2015. Retrieved 2015-11-13.
The 2007 prize also recognizes Green for "his many outstanding results including his resolution of the Cameron-Erdős conjecture..."
- Xue, Jinxin (2014). "Noncollision Singularities in a Planar Four-body Problem" (Document).
{{cite document}}: Cite document requires|publisher=(help); Unknown parameter|arxiv=ignored (help) - Xue, Jinxin (2020). "Non-collision singularities in a planar 4-body problem". Acta Mathematica. 224 (2): 253–388. doi:10.4310/ACTA.2020.v224.n2.a2. S2CID 226420221.
- Bowditch, Brian H. (2006). "The angel game in the plane" (PDF). School of Mathematics, University of Southampton: warwick.ac.uk Warwick University. Archived (PDF) from the original on 2016-03-04. Retrieved 2016-03-18.
- Kloster, Oddvar. "A Solution to the Angel Problem" (PDF). SINTEF ICT, Postboks 124 Blindern, 0314 Oslo, Norway. Archived from the original (PDF) on 2016-01-07. Retrieved 2016-03-18.
{{cite web}}: CS1 maint: location (link) - Mathe, Andras (2007). "The Angel of power 2 wins" (PDF). Combinatorics, Probability and Computing. 16 (3): 363–374. doi:10.1017/S0963548306008303. S2CID 16892955. Archived (PDF) from the original on 2016-10-13. Retrieved 2016-03-18.
- Gacs, Peter. "THE ANGEL WINS" (PDF). Archived (PDF) from the original on 2016-03-04. Retrieved 2016-03-18.
- Song, Antoine. "Existence of infinitely many minimal hypersurfaces in closed manifolds" (PDF). www.ams.org. Retrieved 19 June 2021.
..I will present a solution of the conjecture, which builds on min-max methods developed by F. C. Marques and A. Neves..
- "Antoine Song | Clay Mathematics Institute".
...Building on work of Codá Marques and Neves, in 2018 Song proved Yau's conjecture in complete generality
- Wolchover, Natalie (July 11, 2017), "Pentagon Tiling Proof Solves Century-Old Math Problem", Quanta Magazine, archived from the original on August 6, 2017, retrieved July 18, 2017
- Marques, Fernando C.; Neves, André (2013). "Min-max theory and the Willmore conjecture". Annals of Mathematics. 179 (2): 683–782. arXiv:1202.6036. doi:10.4007/annals.2014.179.2.6. S2CID 50742102.
- Guth, Larry; Katz, Nets Hawk (2015). "On the Erdos distinct distance problem in the plane". Annals of Mathematics. 181 (1): 155–190. arXiv:1011.4105. doi:10.4007/annals.2015.181.1.2.
- Henle, Frederick V.; Henle, James M. "Squaring the Plane" (PDF). www.maa.org Mathematics Association of America. Archived (PDF) from the original on 2016-03-24. Retrieved 2016-03-18.
- Brock, Jeffrey F.; Canary, Richard D.; Minsky, Yair N. (2012). "The classification of Kleinian surface groups, II: The Ending Lamination Conjecture". Annals of Mathematics. 176 (1): 1–149. arXiv:math/0412006. doi:10.4007/annals.2012.176.1.1.
- Connelly, Robert; Demaine, Erik D.; Rote, Günter (2003), "Straightening polygonal arcs and convexifying polygonal cycles" (PDF), Discrete & Computational Geometry, 30 (2): 205–239, doi:10.1007/s00454-003-0006-7, MR 1931840, S2CID 40382145
- Shestakov, Ivan P.; Umirbaev, Ualbai U. (2004). "The tame and the wild automorphisms of polynomial rings in three variables". Journal of the American Mathematical Society. 17 (1): 197–227. doi:10.1090/S0894-0347-03-00440-5. MR 2015334.
- Hutchings, Michael; Morgan, Frank; Ritoré, Manuel; Ros, Antonio (2002). "Proof of the double bubble conjecture". Annals of Mathematics. Second Series. 155 (2): 459–489. arXiv:math/0406017. doi:10.2307/3062123. hdl:10481/32449. JSTOR 3062123. MR 1906593.
- Hales, Thomas C. (2001). "The Honeycomb Conjecture". Discrete & Computational Geometry. 25: 1–22. arXiv:math/9906042. doi:10.1007/s004540010071.
- Ullmo, E (1998). "Positivité et Discrétion des Points Algébriques des Courbes". Annals of Mathematics. 147 (1): 167–179. arXiv:alg-geom/9606017. doi:10.2307/120987. JSTOR 120987. S2CID 119717506. Zbl 0934.14013.
- Zhang, S.-W. (1998). "Equidistribution of small points on abelian varieties". Annals of Mathematics. 147 (1): 159–165. doi:10.2307/120986. JSTOR 120986.
- Hales, Thomas; Adams, Mark; Bauer, Gertrud; Dang, Dat Tat; Harrison, John; Hoang, Le Truong; Kaliszyk, Cezary; Magron, Victor; McLaughlin, Sean; Nguyen, Tat Thang; Nguyen, Quang Truong; Nipkow, Tobias; Obua, Steven; Pleso, Joseph; Rute, Jason; Solovyev, Alexey; Ta, Thi Hoai An; Tran, Nam Trung; Trieu, Thi Diep; Urban, Josef; Ky, Vu; Zumkeller, Roland (2017). "A formal proof of the Kepler conjecture". Forum of Mathematics, Pi. 5: e2. arXiv:1501.02155. doi:10.1017/fmp.2017.1.
- Hales, Thomas C.; McLaughlin, Sean (2010). "The dodecahedral conjecture". Journal of the American Mathematical Society. 23 (2): 299–344. arXiv:math/9811079. Bibcode:2010JAMS...23..299H. doi:10.1090/S0894-0347-09-00647-X.
- Dujmović, Vida; Eppstein, David; Hickingbotham, Robert; Morin, Pat; Wood, David R. (August 2021). "Stack-number is not bounded by queue-number". Combinatorica. 42 (2): 151–164. arXiv:2011.04195. doi:10.1007/s00493-021-4585-7. S2CID 226281691.
- Huang, C.; Kotzig, A.; Rosa, A. (1982). "Further results on tree labellings". Utilitas Mathematica. 21: 31–48. MR 0668845..
- Hartnett, Kevin (19 February 2020). "Rainbow Proof Shows Graphs Have Uniform Parts". Quanta Magazine. Retrieved 2020-02-29.
- Shitov, Yaroslav (1 September 2019). "Counterexamples to Hedetniemi's conjecture". Annals of Mathematics. 190 (2): 663–667. arXiv:1905.02167. doi:10.4007/annals.2019.190.2.6. JSTOR 10.4007/annals.2019.190.2.6. MR 3997132. S2CID 146120733. Zbl 1451.05087. Retrieved 19 July 2021.
- Abdollahi A., Zallaghi M. (2015). "Character sums for Cayley graphs". Communications in Algebra. 43 (12): 5159–5167. doi:10.1080/00927872.2014.967398. S2CID 117651702.
- Chalopin, Jérémie; Gonçalves, Daniel (2009). "Every planar graph is the intersection graph of segments in the plane: extended abstract". In Mitzenmacher, Michael (ed.). Proceedings of the 41st Annual ACM Symposium on Theory of Computing, STOC 2009, Bethesda, MD, USA, May 31 - June 2, 2009. ACM. pp. 631–638. doi:10.1145/1536414.1536500.
- Aharoni, Ron; Berger, Eli (2009). "Menger's theorem for infinite graphs". Inventiones Mathematicae. 176 (1): 1–62. arXiv:math/0509397. Bibcode:2009InMat.176....1A. doi:10.1007/s00222-008-0157-3.
- Seigel-Itzkovich, Judy (2008-02-08). "Russian immigrant solves math puzzle". The Jerusalem Post. Retrieved 2015-11-12.
- "Graph Theory". Archived from the original on 2016-03-08. Retrieved 2016-03-18.
- Chudnovsky, Maria; Robertson, Neil; Seymour, Paul; Thomas, Robin (2002). "The strong perfect graph theorem". Annals of Mathematics. 164: 51–229. arXiv:math/0212070. Bibcode:2002math.....12070C. doi:10.4007/annals.2006.164.51. S2CID 119151552.
- Joel Friedman, "Sheaves on Graphs, Their Homological Invariants, and a Proof of the Hanna Neumann Conjecture: With an Appendix by Warren Dicks" Mem. Amer. Math. Soc., 233 (2015), no. 1100.
- Mineyev, Igor (2012). "Submultiplicativity and the Hanna Neumann conjecture". Annals of Mathematics. Second Series. 175 (1): 393–414. doi:10.4007/annals.2012.175.1.11. MR 2874647.
- Namazi, Hossein; Souto, Juan (2012). "Non-realizability and ending laminations: Proof of the density conjecture". Acta Mathematica. 209 (2): 323–395. doi:10.1007/s11511-012-0088-0.
- Bourgain, Jean; Ciprian, Demeter; Larry, Guth (2015). "Proof of the main conjecture in Vinogradov's Mean Value Theorem for degrees higher than three". Annals of Mathematics. 184 (2): 633–682. arXiv:1512.01565. Bibcode:2015arXiv151201565B. doi:10.4007/annals.2016.184.2.7. hdl:1721.1/115568. S2CID 43929329.
- Helfgott, Harald A. (2013). "Major arcs for Goldbach's theorem". arXiv:1305.2897 .
- Helfgott, Harald A. (2012). "Minor arcs for Goldbach's problem". arXiv:1205.5252 .
- Helfgott, Harald A. (2013). "The ternary Goldbach conjecture is true". arXiv:1312.7748 .
- Zhang, Yitang (2014-05-01). "Bounded gaps between primes". Annals of Mathematics. 179 (3): 1121–1174. doi:10.4007/annals.2014.179.3.7. ISSN 0003-486X.
- "Bounded gaps between primes - Polymath Wiki". asone.ai. Retrieved 2021-08-27.
- Maynard, James (2015-01-01). "Small gaps between primes". Annals of Mathematics: 383–413. arXiv:1311.4600. doi:10.4007/annals.2015.181.1.7. ISSN 0003-486X. S2CID 55175056.
- Cilleruelo, Javier (2010). "Generalized Sidon sets". Advances in Mathematics. 225 (5): 2786–2807. doi:10.1016/j.aim.2010.05.010. hdl:10261/31032. S2CID 7385280.
- Khare, Chandrashekhar; Wintenberger, Jean-Pierre (2009), "Serre's modularity conjecture (I)", Inventiones Mathematicae, 178 (3): 485–504, Bibcode:2009InMat.178..485K, CiteSeerX 10.1.1.518.4611, doi:10.1007/s00222-009-0205-7, S2CID 14846347
- Khare, Chandrashekhar; Wintenberger, Jean-Pierre (2009), "Serre's modularity conjecture (II)", Inventiones Mathematicae, 178 (3): 505–586, Bibcode:2009InMat.178..505K, CiteSeerX 10.1.1.228.8022, doi:10.1007/s00222-009-0206-6, S2CID 189820189
- "2011 Cole Prize in Number Theory" (PDF). Notices of the AMS. 58 (4): 610–611. ISSN 1088-9477. OCLC 34550461. Archived (PDF) from the original on 2015-11-06. Retrieved 2015-11-12.
- "Bombieri and Tao Receive King Faisal Prize" (PDF). Notices of the AMS. 57 (5): 642–643. May 2010. ISSN 1088-9477. OCLC 34550461. Archived (PDF) from the original on 2016-03-04. Retrieved 2016-03-18.
Working with Ben Green, he proved there are arbitrarily long arithmetic progressions of prime numbers—a result now known as the Green–Tao theorem.
- Metsänkylä, Tauno (5 September 2003). "Catalan's conjecture: another old diophantine problem solved" (PDF). Bulletin of the American Mathematical Society. 41 (1): 43–57. doi:10.1090/s0273-0979-03-00993-5. ISSN 0273-0979. Archived (PDF) from the original on 4 March 2016. Retrieved 13 November 2015.
The conjecture, which dates back to 1844, was recently proven by the Swiss mathematician Preda Mihăilescu.
- Croot, Ernest S., III (2000). Unit Fractions. Ph.D. thesis. University of Georgia, Athens.
{{cite book}}: CS1 maint: multiple names: authors list (link) Croot, Ernest S., III (2003). "On a coloring conjecture about unit fractions". Annals of Mathematics. 157 (2): 545–556. arXiv:math.NT/0311421. Bibcode:2003math.....11421C. doi:10.4007/annals.2003.157.545. S2CID 13514070.{{cite journal}}: CS1 maint: multiple names: authors list (link) - Lafforgue, Laurent (1998), "Chtoucas de Drinfeld et applications" [Drinfelʹd shtukas and applications], Documenta Mathematica (in French), II: 563–570, ISSN 1431-0635, MR 1648105, archived from the original on 2018-04-27, retrieved 2016-03-18
- Wiles, Andrew (1995). "Modular elliptic curves and Fermat's Last Theorem" (PDF). Annals of Mathematics. 141 (3): 443–551. CiteSeerX 10.1.1.169.9076. doi:10.2307/2118559. JSTOR 2118559. OCLC 37032255. Archived (PDF) from the original on 2011-05-10. Retrieved 2016-03-06.
- Taylor R, Wiles A (1995). "Ring theoretic properties of certain Hecke algebras". Annals of Mathematics. 141 (3): 553–572. CiteSeerX 10.1.1.128.531. doi:10.2307/2118560. JSTOR 2118560. OCLC 37032255. Archived from the original on 16 September 2000.
- Lee, Choongbum (2017). "Ramsey numbers of degenerate graphs". Annals of Mathematics. 185 (3): 791–829. arXiv:1505.04773. doi:10.4007/annals.2017.185.3.2. S2CID 7974973.
- Lamb, Evelyn (26 May 2016). "Two-hundred-terabyte maths proof is largest ever". Nature. 534 (7605): 17–18. Bibcode:2016Natur.534...17L. doi:10.1038/nature.2016.19990. PMID 27251254.
- Heule, Marijn J. H.; Kullmann, Oliver; Marek, Victor W. (2016). "Solving and Verifying the Boolean Pythagorean Triples Problem via Cube-and-Conquer". In Creignou, N.; Le Berre, D. (eds.). Theory and Applications of Satisfiability Testing – SAT 2016. Lecture Notes in Computer Science. Vol. 9710. Springer, . pp. 228–245. arXiv:1605.00723. doi:10.1007/978-3-319-40970-2_15. ISBN 978-3-319-40969-6. MR 3534782. S2CID 7912943.
- Linkletter, David (27 December 2019). "The 10 Biggest Math Breakthroughs of 2019". www.popularmechanics.com. Hearst Digital Media. Retrieved 20 June 2021.
- Piccirillo, Lisa (2020). "The Conway knot is not slice". Annals of Mathematics. 191: 581–591. doi:10.4007/annals.2020.191.2.5.
- Klarreich, Erica (2020-05-19). "Graduate Student Solves Decades-Old Conway Knot Problem". Quanta Magazine. Retrieved 2022-08-17.
- Agol, Ian (2013). "The virtual Haken conjecture (with an appendix by Ian Agol, Daniel Groves, and Jason Manning)" (PDF). Documenta Mathematica. 18: 1045–1087. arXiv:1204.2810v1.
- Brendle, Simon (2013). "Embedded minimal tori in and the Lawson conjecture". Acta Mathematica. 211 (2): 177–190. arXiv:1203.6597. doi:10.1007/s11511-013-0101-2.
- Kahn, Jeremy; Markovic, Vladimir (2015). "The good pants homology and the Ehrenpreis conjecture". Annals of Mathematics. 182 (1): 1–72. arXiv:1101.1330. doi:10.4007/annals.2015.182.1.1.
- Austin, Tim (December 2013). "Rational group ring elements with kernels having irrational dimension". Proceedings of the London Mathematical Society. 107 (6): 1424–1448. arXiv:0909.2360. Bibcode:2009arXiv0909.2360A. doi:10.1112/plms/pdt029. S2CID 115160094.
- Lurie, Jacob (2009). "On the classification of topological field theories". Current Developments in Mathematics. 2008: 129–280. arXiv:0905.0465. Bibcode:2009arXiv0905.0465L. doi:10.4310/cdm.2008.v2008.n1.a3. S2CID 115162503.
- ^ "Prize for Resolution of the Poincaré Conjecture Awarded to Dr. Grigoriy Perelman" (PDF) (Press release). Clay Mathematics Institute. March 18, 2010. Archived from the original on March 22, 2010. Retrieved November 13, 2015.
The Clay Mathematics Institute hereby awards the Millennium Prize for resolution of the Poincaré conjecture to Grigoriy Perelman.
- Morgan, John; Tian, Gang (2008). "Completion of the Proof of the Geometrization Conjecture". arXiv:0809.4040 .
- Norio Iwase (1 November 1998). "Ganea's Conjecture on Lusternik-Schnirelmann Category". ResearchGate.
- Tao, Terence (2015). "The Erdős discrepancy problem". arXiv:1509.05363v5 .
- Duncan, John F. R.; Griffin, Michael J.; Ono, Ken (1 December 2015). "Proof of the umbral moonshine conjecture". Research in the Mathematical Sciences. 2 (1): 26. arXiv:1503.01472. Bibcode:2015arXiv150301472D. doi:10.1186/s40687-015-0044-7. S2CID 43589605.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - Cheeger, Jeff; Naber, Aaron (2015). "Regularity of Einstein Manifolds and the Codimension 4 Conjecture". Annals of Mathematics. 182 (3): 1093–1165. arXiv:1406.6534. doi:10.4007/annals.2015.182.3.5.
- Wolchover, Natalie (March 28, 2017). "A Long-Sought Proof, Found and Almost Lost". Quanta Magazine. Archived from the original on April 24, 2017. Retrieved May 2, 2017.
- Newman, Alantha; Nikolov, Aleksandar (2011). "A counterexample to Beck's conjecture on the discrepancy of three permutations". arXiv:1104.2922 .
- Voevodsky, Vladimir (1 July 2011). "On motivic cohomology with Z/l-coefficients" (PDF). School of Mathematics Institute for Advanced Study Einstein Drive Princeton, NJ 08540: annals.math.princeton.edu (Princeton University). pp. 401–438. Archived (PDF) from the original on 2016-03-27. Retrieved 2016-03-18.
{{cite web}}: CS1 maint: location (link) - Geisser, Thomas; Levine, Marc (2001). "The Bloch-Kato conjecture and a theorem of Suslin-Voevodsky". Journal für die Reine und Angewandte Mathematik. 2001 (530): 55–103. doi:10.1515/crll.2001.006. MR 1807268.
- Kahn, Bruno. "Algebraic K-Theory, Algebraic Cycles and Arithmetic Geometry" (PDF). webusers.imj-prg.fr. Archived (PDF) from the original on 2016-03-27. Retrieved 2016-03-18.
- "motivic cohomology – Milnor–Bloch–Kato conjecture implies the Beilinson-Lichtenbaum conjecture – MathOverflow". Retrieved 2016-03-18.
- Mattman, Thomas W.; Solis, Pablo (2009). "A proof of the Kauffman-Harary Conjecture". Algebraic & Geometric Topology. 9 (4): 2027–2039. arXiv:0906.1612. Bibcode:2009arXiv0906.1612M. doi:10.2140/agt.2009.9.2027. S2CID 8447495.
- Kahn, Jeremy; Markovic, Vladimir (2012). "Immersing almost geodesic surfaces in a closed hyperbolic three manifold". Annals of Mathematics. 175 (3): 1127–1190. arXiv:0910.5501. doi:10.4007/annals.2012.175.3.4.
- Lu, Zhiqin (September 2011) . "Normal Scalar Curvature Conjecture and its applications". Journal of Functional Analysis. 261 (5): 1284–1308. arXiv:0711.3510. doi:10.1016/j.jfa.2011.05.002.
- Dencker, Nils (2006), "The resolution of the Nirenberg–Treves conjecture" (PDF), Annals of Mathematics, 163 (2): 405–444, doi:10.4007/annals.2006.163.405, S2CID 16630732, archived (PDF) from the original on 2018-07-20, retrieved 2019-04-07
- "Research Awards". Clay Mathematics Institute. Archived from the original on 2019-04-07. Retrieved 2019-04-07.
- Lewis, A. S.; Parrilo, P. A.; Ramana, M. V. (2005). "The Lax conjecture is true". Proceedings of the American Mathematical Society. 133 (9): 2495–2499. doi:10.1090/S0002-9939-05-07752-X. MR 2146191. S2CID 17436983.
- "Fields Medal – Ngô Bảo Châu". International Congress of Mathematicians 2010. ICM. 19 August 2010. Archived from the original on 24 September 2015. Retrieved 2015-11-12.
Ngô Bảo Châu is being awarded the 2010 Fields Medal for his proof of the Fundamental Lemma in the theory of automorphic forms through the introduction of new algebro-geometric methods.
- Voevodsky, Vladimir (2003). "Reduced power operations in motivic cohomology" (PDF). Publications Mathématiques de l'IHÉS. 98: 1–57. arXiv:math/0107109. CiteSeerX 10.1.1.170.4427. doi:10.1007/s10240-003-0009-z. S2CID 8172797. Archived from the original on 2017-07-28. Retrieved 2016-03-18.
- Baruch, Ehud Moshe (2003). "A proof of Kirillov's conjecture". Annals of Mathematics. Second Series. 158 (1): 207–252. doi:10.4007/annals.2003.158.207. MR 1999922.
- Haas, Bertrand. "A Simple Counterexample to Kouchnirenko's Conjecture" (PDF). Archived (PDF) from the original on 2016-10-07. Retrieved 2016-03-18.
- Haiman, Mark (2001). "Hilbert schemes, polygraphs and the Macdonald positivity conjecture". Journal of the American Mathematical Society. 14 (4): 941–1006. doi:10.1090/S0894-0347-01-00373-3. MR 1839919. S2CID 9253880.
- Auscher, Pascal; Hofmann, Steve; Lacey, Michael; McIntosh, Alan; Tchamitchian, Ph. (2002). "The solution of the Kato square root problem for second order elliptic operators on ". Annals of Mathematics. Second Series. 156 (2): 633–654. doi:10.2307/3597201. JSTOR 3597201. MR 1933726.
- Barbieri-Viale, Luca; Rosenschon, Andreas; Saito, Morihiko (2003). "Deligne's Conjecture on 1-Motives". Annals of Mathematics. 158 (2): 593–633. arXiv:math/0102150. doi:10.4007/annals.2003.158.593.
- Breuil, Christophe; Conrad, Brian; Diamond, Fred; Taylor, Richard (2001), "On the modularity of elliptic curves over Q: wild 3-adic exercises", Journal of the American Mathematical Society, 14 (4): 843–939, doi:10.1090/S0894-0347-01-00370-8, ISSN 0894-0347, MR 1839918
- Luca, Florian (2000). "On a conjecture of Erdős and Stewart" (PDF). Mathematics of Computation. 70 (234): 893–897. Bibcode:2001MaCom..70..893L. doi:10.1090/s0025-5718-00-01178-9. Archived (PDF) from the original on 2016-04-02. Retrieved 2016-03-18.
- Atiyah, Michael (2000). "The geometry of classical particles". In Yau, Shing-Tung (ed.). Papers dedicated to Atiyah, Bott, Hirzebruch, and Singer. Surveys in Differential Geometry. Vol. 7. Somerville, Massachusetts: International Press. pp. 1–15. doi:10.4310/SDG.2002.v7.n1.a1. MR 1919420.
- Merel, Loïc (1996). ""Bornes pour la torsion des courbes elliptiques sur les corps de nombres" ". Inventiones Mathematicae. 124 (1): 437–449. Bibcode:1996InMat.124..437M. doi:10.1007/s002220050059. MR 1369424. S2CID 3590991.
- Chen, Zhibo (1996). "Harary's conjectures on integral sum graphs". Discrete Mathematics. 160 (1–3): 241–244. doi:10.1016/0012-365X(95)00163-Q.
Further reading
Books discussing problems solved since 1995
- Singh, Simon (2002). Fermat's Last Theorem. Fourth Estate. ISBN 978-1-84115-791-7.
- O'Shea, Donal (2007). The Poincaré Conjecture. Penguin. ISBN 978-1-84614-012-9.
- Szpiro, George G. (2003). Kepler's Conjecture. Wiley. ISBN 978-0-471-08601-7.
- Ronan, Mark (2006). Symmetry and the Monster. Oxford. ISBN 978-0-19-280722-9.
Books discussing unsolved problems
- Chung, Fan; Graham, Ron (1999). Erdös on Graphs: His Legacy of Unsolved Problems. AK Peters. ISBN 978-1-56881-111-6.
- Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1994). Unsolved Problems in Geometry. Springer. ISBN 978-0-387-97506-1.
- Guy, Richard K. (2004). Unsolved Problems in Number Theory. Springer. ISBN 978-0-387-20860-2.
- Klee, Victor; Wagon, Stan (1996). Old and New Unsolved Problems in Plane Geometry and Number Theory. The Mathematical Association of America. ISBN 978-0-88385-315-3.
- du Sautoy, Marcus (2003). The Music of the Primes: Searching to Solve the Greatest Mystery in Mathematics. Harper Collins. ISBN 978-0-06-093558-0.
- Derbyshire, John (2003). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. Joseph Henry Press. ISBN 978-0-309-08549-6.
- Devlin, Keith (2006). The Millennium Problems – The Seven Greatest Unsolved* Mathematical Puzzles Of Our Time. Barnes & Noble. ISBN 978-0-7607-8659-8.
- Blondel, Vincent D.; Megrestski, Alexandre (2004). Unsolved problems in mathematical systems and control theory. Princeton University Press. ISBN 978-0-691-11748-5.
- Ji, Lizhen; Poon, Yat-Sun; Yau, Shing-Tung (2013). Open Problems and Surveys of Contemporary Mathematics (volume 6 in the Surveys in Modern Mathematics series) (Surveys of Modern Mathematics). International Press of Boston. ISBN 978-1-57146-278-7.
- Waldschmidt, Michel (2004). "Open Diophantine Problems" (PDF). Moscow Mathematical Journal. 4 (1): 245–305. arXiv:math/0312440. doi:10.17323/1609-4514-2004-4-1-245-305. ISSN 1609-3321. S2CID 11845578. Zbl 1066.11030.
- Mazurov, V. D.; Khukhro, E. I. (1 Jun 2015). "Unsolved Problems in Group Theory. The Kourovka Notebook. No. 18 (English version)". arXiv:1401.0300v6 .
External links
- 24 Unsolved Problems and Rewards for them
- List of links to unsolved problems in mathematics, prizes and research
- Open Problem Garden
- AIM Problem Lists
- Unsolved Problem of the Week Archive. MathPro Press.
- Ball, John M. "Some Open Problems in Elasticity" (PDF).
- Constantin, Peter. "Some open problems and research directions in the mathematical study of fluid dynamics" (PDF).
- Serre, Denis. "Five Open Problems in Compressible Mathematical Fluid Dynamics" (PDF).
- Unsolved Problems in Number Theory, Logic and Cryptography
- 200 open problems in graph theory
- The Open Problems Project (TOPP), discrete and computational geometry problems
- Kirby's list of unsolved problems in low-dimensional topology
- Erdös' Problems on Graphs
- Unsolved Problems in Virtual Knot Theory and Combinatorial Knot Theory
- Open problems from the 12th International Conference on Fuzzy Set Theory and Its Applications
- List of open problems in inner model theory
- Aizenman, Michael. "Open Problems in Mathematical Physics".
- Barry Simon's 15 Problems in Mathematical Physics
| Well-known unsolved problems by discipline | |
|---|---|
 applied to a complex matrix
applied to a complex matrix  is at most twice the
is at most twice the  over the
over the  .
. , a
, a  exists.
exists. , then it has no nil
, then it has no nil  is the maximum of a finite set of minimums of finite collections of polynomials.
is the maximum of a finite set of minimums of finite collections of polynomials. with
with  , it is possible to create an
, it is possible to create an  matrix whose rows are
matrix whose rows are  has all roots in the closed
has all roots in the closed  from some
from some  is a
is a  is zero.
is zero. over
over  have at most some bounded number
have at most some bounded number  of
of  with
with  , if the
, if the 

 (the
(the  ,
,  runners with pairwise distinct speeds run round a track of unit length, will every runner be "lonely" (that is, be at least a distance
runners with pairwise distinct speeds run round a track of unit length, will every runner be "lonely" (that is, be at least a distance  from each other runner) at some time?
from each other runner) at some time? sets be bounded by an exponential function in
sets be bounded by an exponential function in  ?
? for
for  .
.
 conjecture)
conjecture) action on the circle either Lebesgue or atomic?
action on the circle either Lebesgue or atomic? constructed from a
constructed from a  on a
on a  and the
and the  of
of 
 circles in an equilateral triangle requires a triangle of the same size as packing
circles in an equilateral triangle requires a triangle of the same size as packing  is
is  points can be equidistant in
points can be equidistant in  spaces
spaces

 in
in  must have a distance set of nonzero
must have a distance set of nonzero  , what is the largest graph of diameter
, what is the largest graph of diameter  ?
? embeddings with bounded distortion
embeddings with bounded distortion
 -vertex tournament contain as a subgraph every
-vertex tournament contain as a subgraph every  is finite; in its
is finite; in its  are finite remains open.
are finite remains open. is a simple algebraic group over an algebraically closed field.
is a simple algebraic group over an algebraically closed field. -saturated models of a countable theory.
-saturated models of a countable theory. : If a sentence is categorical above the Hanf number then it is categorical in all cardinals above the Hanf number.
: If a sentence is categorical above the Hanf number then it is categorical in all cardinals above the Hanf number. there exists a cardinal
there exists a cardinal  such that if an
such that if an  .
. does it have a model of cardinality continuum?
does it have a model of cardinality continuum? , is it categorical in every cardinal?
, is it categorical in every cardinal?
 ,
,  is true for only finitely many positive
is true for only finitely many positive  such that
such that  .
. such that, for any elliptic curve
such that, for any elliptic curve  defined over
defined over  with minimal discriminant
with minimal discriminant  and conductor
and conductor  .
. with real
with real  ?
?
 other than
other than  ?
? -th derivative, then must
-th derivative, then must  the only solution to the
the only solution to the  , there are positive integers
, there are positive integers  such that
such that  .
. is an
is an  where
where  and
and  .
. such that either
such that either  or
or  .
. divides
divides 
 ,
,  , where
, where  is the distance from
is the distance from  to the nearest integer.
to the nearest integer. are less than
are less than  for all positive integers
for all positive integers  , the equation
, the equation  has finitely many solutions when
has finitely many solutions when  are not both
are not both 

 is at most
is at most  a
a  where
where  , all three numbers
, all three numbers  is an
is an  to the equation
to the equation  with
with  being positive integers satisfying
being positive integers satisfying  .
.
 .
. can be represented as the sum of an odd
can be represented as the sum of an odd 
 is within a constant multiple of
is within a constant multiple of 
 .
.
 , then it is a
, then it is a 
 and
and  .
. where
where  with each
with each  , there are infinitely many
, there are infinitely many  is the sum of two
is the sum of two  ,
,  does not divide
does not divide 
 or
or  ,
,  is prime, and
is prime, and  is prime are true, then the third condition is true.
is prime are true, then the third condition is true. of nonconstant
of nonconstant  are all
are all  which, for all
which, for all  .
. ?
? and
and  simultaneously?
simultaneously? , with gcd(k, c) = 1 and gcd(b, c) = 1, are there infinitely many primes of the form
, with gcd(k, c) = 1 and gcd(b, c) = 1, are there infinitely many primes of the form  with integer n ≥ 1?
with integer n ≥ 1? composite for
composite for  ?
?
 (see
(see  ?
?
 and
and  conjectures, Bourgain-Tzafriri conjecture and
conjectures, Bourgain-Tzafriri conjecture and  -conjecture)
-conjecture) and the Lawson conjecture"
and the Lawson conjecture" ". Annals of Mathematics. Second Series. 156 (2): 633–654.
". Annals of Mathematics. Second Series. 156 (2): 633–654.