 An O-core transformer consisting of two coils of copper wire wrapped around a magnetic core An O-core transformer consisting of two coils of copper wire wrapped around a magnetic core | |
| Type | Passive |
|---|---|
| Working principle | Electromagnetic induction |
| Inventor | Nicholas Callan Charles G. Page |
| Invention year | 1836; 188 years ago (1836) |
| Electronic symbol | |
 | |
In electrical engineering, a transformer is a passive component that transfers electrical energy from one electrical circuit to another circuit, or multiple circuits. A varying current in any coil of the transformer produces a varying magnetic flux in the transformer's core, which induces a varying electromotive force (EMF) across any other coils wound around the same core. Electrical energy can be transferred between separate coils without a metallic (conductive) connection between the two circuits. Faraday's law of induction, discovered in 1831, describes the induced voltage effect in any coil due to a changing magnetic flux encircled by the coil.
Transformers are used to change AC voltage levels, such transformers being termed step-up or step-down type to increase or decrease voltage level, respectively. Transformers can also be used to provide galvanic isolation between circuits as well as to couple stages of signal-processing circuits. Since the invention of the first constant-potential transformer in 1885, transformers have become essential for the transmission, distribution, and utilization of alternating current electric power. A wide range of transformer designs is encountered in electronic and electric power applications. Transformers range in size from RF transformers less than a cubic centimeter in volume, to units weighing hundreds of tons used to interconnect the power grid.
Principles
Ideal transformer equations
By Faraday's law of induction:
| (Eq. 1) |
| (Eq. 2) |
where is the instantaneous voltage, is the number of turns in a winding, dΦ/dt is the derivative of the magnetic flux Φ through one turn of the winding over time (t), and subscripts P and S denotes primary and secondary.
Combining the ratio of eq. 1 & eq. 2:
| Turns ratio | (Eq. 3) |
where for a step-up transformer a < 1 and for a step-down transformer a > 1.
By the law of conservation of energy, apparent, real and reactive power are each conserved in the input and output:
| (Eq. 4) |
where is apparent power and is current.
Combining Eq. 3 & Eq. 4 with this endnote gives the ideal transformer identity:
| (Eq. 5) |
where is winding self-inductance.
By Ohm's law and ideal transformer identity:
| (Eq. 6) |
| (Eq. 7) |
Ideal transformer
An ideal transformer is linear, lossless and perfectly coupled. Perfect coupling implies infinitely high core magnetic permeability and winding inductance and zero net magnetomotive force (i.e. ipnp − isns = 0).

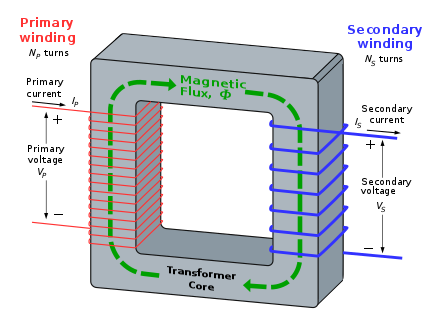
A varying current in the transformer's primary winding creates a varying magnetic flux in the transformer core, which is also encircled by the secondary winding. This varying flux at the secondary winding induces a varying electromotive force or voltage in the secondary winding. This electromagnetic induction phenomenon is the basis of transformer action and, in accordance with Lenz's law, the secondary current so produced creates a flux equal and opposite to that produced by the primary winding.
The windings are wound around a core of infinitely high magnetic permeability so that all of the magnetic flux passes through both the primary and secondary windings. With a voltage source connected to the primary winding and a load connected to the secondary winding, the transformer currents flow in the indicated directions and the core magnetomotive force cancels to zero.
According to Faraday's law, since the same magnetic flux passes through both the primary and secondary windings in an ideal transformer, a voltage is induced in each winding proportional to its number of turns. The transformer winding voltage ratio is equal to the winding turns ratio.
An ideal transformer is a reasonable approximation for a typical commercial transformer, with voltage ratio and winding turns ratio both being inversely proportional to the corresponding current ratio.
The load impedance referred to the primary circuit is equal to the turns ratio squared times the secondary circuit load impedance.
Real transformer
Deviations from ideal transformer
The ideal transformer model neglects many basic linear aspects of real transformers, including unavoidable losses and inefficiencies.
(a) Core losses, collectively called magnetizing current losses, consisting of
- Hysteresis losses due to nonlinear magnetic effects in the transformer core, and
- Eddy current losses due to joule heating in the core that are proportional to the square of the transformer's applied voltage.
(b) Unlike the ideal model, the windings in a real transformer have non-zero resistances and inductances associated with:
- Joule losses due to resistance in the primary and secondary windings
- Leakage flux that escapes from the core and passes through one winding only resulting in primary and secondary reactive impedance.
(c) similar to an inductor, parasitic capacitance and self-resonance phenomenon due to the electric field distribution. Three kinds of parasitic capacitance are usually considered and the closed-loop equations are provided
- Capacitance between adjacent turns in any one layer;
- Capacitance between adjacent layers;
- Capacitance between the core and the layer(s) adjacent to the core;
Inclusion of capacitance into the transformer model is complicated, and is rarely attempted; the 'real' transformer model's equivalent circuit shown below does not include parasitic capacitance. However, the capacitance effect can be measured by comparing open-circuit inductance, i.e. the inductance of a primary winding when the secondary circuit is open, to a short-circuit inductance when the secondary winding is shorted.
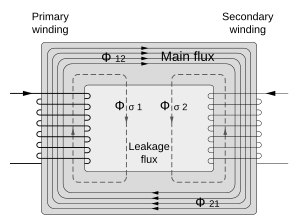
Leakage flux
Main article: Leakage inductanceThe ideal transformer model assumes that all flux generated by the primary winding links all the turns of every winding, including itself. In practice, some flux traverses paths that take it outside the windings. Such flux is termed leakage flux, and results in leakage inductance in series with the mutually coupled transformer windings. Leakage flux results in energy being alternately stored in and discharged from the magnetic fields with each cycle of the power supply. It is not directly a power loss, but results in inferior voltage regulation, causing the secondary voltage not to be directly proportional to the primary voltage, particularly under heavy load. Transformers are therefore normally designed to have very low leakage inductance.
In some applications increased leakage is desired, and long magnetic paths, air gaps, or magnetic bypass shunts may deliberately be introduced in a transformer design to limit the short-circuit current it will supply. Leaky transformers may be used to supply loads that exhibit negative resistance, such as electric arcs, mercury- and sodium- vapor lamps and neon signs or for safely handling loads that become periodically short-circuited such as electric arc welders.
Air gaps are also used to keep a transformer from saturating, especially audio-frequency transformers in circuits that have a DC component flowing in the windings. A saturable reactor exploits saturation of the core to control alternating current.
Knowledge of leakage inductance is also useful when transformers are operated in parallel. It can be shown that if the percent impedance and associated winding leakage reactance-to-resistance (X/R) ratio of two transformers were the same, the transformers would share the load power in proportion to their respective ratings. However, the impedance tolerances of commercial transformers are significant. Also, the impedance and X/R ratio of different capacity transformers tends to vary.
Equivalent circuit
See also: Steinmetz equivalent circuitReferring to the diagram, a practical transformer's physical behavior may be represented by an equivalent circuit model, which can incorporate an ideal transformer.
Winding joule losses and leakage reactance are represented by the following series loop impedances of the model:
- Primary winding: RP, XP
- Secondary winding: RS, XS.
In normal course of circuit equivalence transformation, RS and XS are in practice usually referred to the primary side by multiplying these impedances by the turns ratio squared, (NP/NS) = a.

Core loss and reactance is represented by the following shunt leg impedances of the model:
- Core or iron losses: RC
- Magnetizing reactance: XM.
RC and XM are collectively termed the magnetizing branch of the model.
Core losses are caused mostly by hysteresis and eddy current effects in the core and are proportional to the square of the core flux for operation at a given frequency. The finite permeability core requires a magnetizing current IM to maintain mutual flux in the core. Magnetizing current is in phase with the flux, the relationship between the two being non-linear due to saturation effects. However, all impedances of the equivalent circuit shown are by definition linear and such non-linearity effects are not typically reflected in transformer equivalent circuits. With sinusoidal supply, core flux lags the induced EMF by 90°. With open-circuited secondary winding, magnetizing branch current I0 equals transformer no-load current.

The resulting model, though sometimes termed 'exact' equivalent circuit based on linearity assumptions, retains a number of approximations. Analysis may be simplified by assuming that magnetizing branch impedance is relatively high and relocating the branch to the left of the primary impedances. This introduces error but allows combination of primary and referred secondary resistances and reactance by simple summation as two series impedances.
Transformer equivalent circuit impedance and transformer ratio parameters can be derived from the following tests: open-circuit test, short-circuit test, winding resistance test, and transformer ratio test.
Transformer EMF equation
If the flux in the core is purely sinusoidal, the relationship for either winding between its rms voltage Erms of the winding, and the supply frequency f, number of turns N, core cross-sectional area A in m and peak magnetic flux density Bpeak in Wb/m or T (tesla) is given by the universal EMF equation:
Polarity
A dot convention is often used in transformer circuit diagrams, nameplates or terminal markings to define the relative polarity of transformer windings. Positively increasing instantaneous current entering the primary winding's 'dot' end induces positive polarity voltage exiting the secondary winding's 'dot' end. Three-phase transformers used in electric power systems will have a nameplate that indicate the phase relationships between their terminals. This may be in the form of a phasor diagram, or using an alpha-numeric code to show the type of internal connection (wye or delta) for each winding.
Effect of frequency
The EMF of a transformer at a given flux increases with frequency. By operating at higher frequencies, transformers can be physically more compact because a given core is able to transfer more power without reaching saturation and fewer turns are needed to achieve the same impedance. However, properties such as core loss and conductor skin effect also increase with frequency. Aircraft and military equipment employ 400 Hz power supplies which reduce core and winding weight. Conversely, frequencies used for some railway electrification systems were much lower (e.g. 16.7 Hz and 25 Hz) than normal utility frequencies (50–60 Hz) for historical reasons concerned mainly with the limitations of early electric traction motors. Consequently, the transformers used to step-down the high overhead line voltages were much larger and heavier for the same power rating than those required for the higher frequencies.
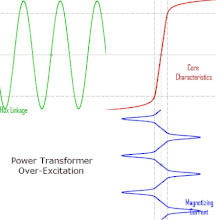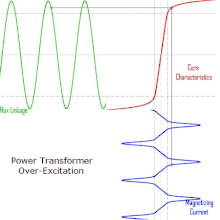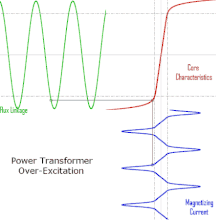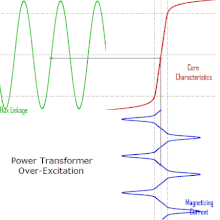
Operation of a transformer at its designed voltage but at a higher frequency than intended will lead to reduced magnetizing current. At a lower frequency, the magnetizing current will increase. Operation of a large transformer at other than its design frequency may require assessment of voltages, losses, and cooling to establish if safe operation is practical. Transformers may require protective relays to protect the transformer from overvoltage at higher than rated frequency.
One example is in traction transformers used for electric multiple unit and high-speed train service operating across regions with different electrical standards. The converter equipment and traction transformers have to accommodate different input frequencies and voltage (ranging from as high as 50 Hz down to 16.7 Hz and rated up to 25 kV).
At much higher frequencies the transformer core size required drops dramatically: a physically small transformer can handle power levels that would require a massive iron core at mains frequency. The development of switching power semiconductor devices made switch-mode power supplies viable, to generate a high frequency, then change the voltage level with a small transformer.
Transformers for higher frequency applications such as SMPS typically use core materials with much lower hysteresis and eddy-current losses than those for 50/60 Hz. Primary examples are iron-powder and ferrite cores. The lower frequency-dependant losses of these cores often is at the expense of flux density at saturation. For instance, ferrite saturation occurs at a substantially lower flux density than laminated iron.
Large power transformers are vulnerable to insulation failure due to transient voltages with high-frequency components, such as caused in switching or by lightning.
Energy losses
Transformer energy losses are dominated by winding and core losses. Transformers' efficiency tends to improve with increasing transformer capacity. The efficiency of typical distribution transformers is between about 98 and 99 percent.
As transformer losses vary with load, it is often useful to tabulate no-load loss, full-load loss, half-load loss, and so on. Hysteresis and eddy current losses are constant at all load levels and dominate at no load, while winding loss increases as load increases. The no-load loss can be significant, so that even an idle transformer constitutes a drain on the electrical supply. Designing energy efficient transformers for lower loss requires a larger core, good-quality silicon steel, or even amorphous steel for the core and thicker wire, increasing initial cost. The choice of construction represents a trade-off between initial cost and operating cost.
Transformer losses arise from:
- Winding joule losses
- Current flowing through a winding's conductor causes joule heating due to the resistance of the wire. As frequency increases, skin effect and proximity effect causes the winding's resistance and, hence, losses to increase.
- Core losses
-
- Hysteresis losses
- Each time the magnetic field is reversed, a small amount of energy is lost due to hysteresis within the core, caused by motion of the magnetic domains within the steel. According to Steinmetz's formula, the heat energy due to hysteresis is given by
- and,
- hysteresis loss is thus given by
- where, f is the frequency, η is the hysteresis coefficient and βmax is the maximum flux density, the empirical exponent of which varies from about 1.4 to 1.8 but is often given as 1.6 for iron. For more detailed analysis, see Magnetic core and Steinmetz's equation.
- Eddy current losses
- Eddy currents are induced in the conductive metal transformer core by the changing magnetic field, and this current flowing through the resistance of the iron dissipates energy as heat in the core. The eddy current loss is a complex function of the square of supply frequency and inverse square of the material thickness. Eddy current losses can be reduced by making the core of a stack of laminations (thin plates) electrically insulated from each other, rather than a solid block; all transformers operating at low frequencies use laminated or similar cores.
- Magnetostriction related transformer hum
- Magnetic flux in a ferromagnetic material, such as the core, causes it to physically expand and contract slightly with each cycle of the magnetic field, an effect known as magnetostriction, the frictional energy of which produces an audible noise known as mains hum or "transformer hum". This transformer hum is especially objectionable in transformers supplied at power frequencies and in high-frequency flyback transformers associated with television CRTs.
- Stray losses
- Leakage inductance is by itself largely lossless, since energy supplied to its magnetic fields is returned to the supply with the next half-cycle. However, any leakage flux that intercepts nearby conductive materials such as the transformer's support structure will give rise to eddy currents and be converted to heat.
- Radiative
- There are also radiative losses due to the oscillating magnetic field but these are usually small.
- Mechanical vibration and audible noise transmission
- In addition to magnetostriction, the alternating magnetic field causes fluctuating forces between the primary and secondary windings. This energy incites vibration transmission in interconnected metalwork, thus amplifying audible transformer hum.
Construction
Cores
Closed-core transformers are constructed in 'core form' or 'shell form'. When windings surround the core, the transformer is core form; when windings are surrounded by the core, the transformer is shell form. Shell form design may be more prevalent than core form design for distribution transformer applications due to the relative ease in stacking the core around winding coils. Core form design tends to, as a general rule, be more economical, and therefore more prevalent, than shell form design for high voltage power transformer applications at the lower end of their voltage and power rating ranges (less than or equal to, nominally, 230 kV or 75 MVA). At higher voltage and power ratings, shell form transformers tend to be more prevalent. Shell form design tends to be preferred for extra-high voltage and higher MVA applications because, though more labor-intensive to manufacture, shell form transformers are characterized as having inherently better kVA-to-weight ratio, better short-circuit strength characteristics and higher immunity to transit damage.
Laminated steel cores


Transformers for use at power or audio frequencies typically have cores made of high permeability silicon steel. The steel has a permeability many times that of free space and the core thus serves to greatly reduce the magnetizing current and confine the flux to a path which closely couples the windings. Early transformer developers soon realized that cores constructed from solid iron resulted in prohibitive eddy current losses, and their designs mitigated this effect with cores consisting of bundles of insulated iron wires. Later designs constructed the core by stacking layers of thin steel laminations, a principle that has remained in use. Each lamination is insulated from its neighbors by a thin non-conducting layer of insulation. The transformer universal EMF equation can be used to calculate the core cross-sectional area for a preferred level of magnetic flux.
The effect of laminations is to confine eddy currents to highly elliptical paths that enclose little flux, and so reduce their magnitude. Thinner laminations reduce losses, but are more laborious and expensive to construct. Thin laminations are generally used on high-frequency transformers, with some of very thin steel laminations able to operate up to 10 kHz.

One common design of laminated core is made from interleaved stacks of E-shaped steel sheets capped with I-shaped pieces, leading to its name of E-I transformer. Such a design tends to exhibit more losses, but is very economical to manufacture. The cut-core or C-core type is made by winding a steel strip around a rectangular form and then bonding the layers together. It is then cut in two, forming two C shapes, and the core assembled by binding the two C halves together with a steel strap. They have the advantage that the flux is always oriented parallel to the metal grains, reducing reluctance.
A steel core's remanence means that it retains a static magnetic field when power is removed. When power is then reapplied, the residual field will cause a high inrush current until the effect of the remaining magnetism is reduced, usually after a few cycles of the applied AC waveform. Overcurrent protection devices such as fuses must be selected to allow this harmless inrush to pass.
On transformers connected to long, overhead power transmission lines, induced currents due to geomagnetic disturbances during solar storms can cause saturation of the core and operation of transformer protection devices.
Distribution transformers can achieve low no-load losses by using cores made with low-loss high-permeability silicon steel or amorphous (non-crystalline) metal alloy. The higher initial cost of the core material is offset over the life of the transformer by its lower losses at light load.
Solid cores
Powdered iron cores are used in circuits such as switch-mode power supplies that operate above mains frequencies and up to a few tens of kilohertz. These materials combine high magnetic permeability with high bulk electrical resistivity. For frequencies extending beyond the VHF band, cores made from non-conductive magnetic ceramic materials called ferrites are common. Some radio-frequency transformers also have movable cores (sometimes called 'slugs') which allow adjustment of the coupling coefficient (and bandwidth) of tuned radio-frequency circuits.
Toroidal cores

Toroidal transformers are built around a ring-shaped core, which, depending on operating frequency, is made from a long strip of silicon steel or permalloy wound into a coil, powdered iron, or ferrite. A strip construction ensures that the grain boundaries are optimally aligned, improving the transformer's efficiency by reducing the core's reluctance. The closed ring shape eliminates air gaps inherent in the construction of an E-I core. The cross-section of the ring is usually square or rectangular, but more expensive cores with circular cross-sections are also available. The primary and secondary coils are often wound concentrically to cover the entire surface of the core. This minimizes the length of wire needed and provides screening to minimize the core's magnetic field from generating electromagnetic interference.
Toroidal transformers are more efficient than the cheaper laminated E-I types for a similar power level. Other advantages compared to E-I types, include smaller size (about half), lower weight (about half), less mechanical hum (making them superior in audio amplifiers), lower exterior magnetic field (about one tenth), low off-load losses (making them more efficient in standby circuits), single-bolt mounting, and greater choice of shapes. The main disadvantages are higher cost and limited power capacity (see Classification parameters below). Because of the lack of a residual gap in the magnetic path, toroidal transformers also tend to exhibit higher inrush current, compared to laminated E-I types.
Ferrite toroidal cores are used at higher frequencies, typically between a few tens of kilohertz to hundreds of megahertz, to reduce losses, physical size, and weight of inductive components. A drawback of toroidal transformer construction is the higher labor cost of winding. This is because it is necessary to pass the entire length of a coil winding through the core aperture each time a single turn is added to the coil. As a consequence, toroidal transformers rated more than a few kVA are uncommon. Relatively few toroids are offered with power ratings above 10 kVA, and practically none above 25 kVA. Small distribution transformers may achieve some of the benefits of a toroidal core by splitting it and forcing it open, then inserting a bobbin containing primary and secondary windings.
Air cores
A transformer can be produced by placing the windings near each other, an arrangement termed an "air-core" transformer. An air-core transformer eliminates loss due to hysteresis in the core material. The magnetizing inductance is drastically reduced by the lack of a magnetic core, resulting in large magnetizing currents and losses if used at low frequencies. Air-core transformers are unsuitable for use in power distribution, but are frequently employed in radio-frequency applications. Air cores are also used for resonant transformers such as Tesla coils, where they can achieve reasonably low loss despite the low magnetizing inductance.
Windings


White: Air, liquid or other insulating medium
Green spiral: Grain oriented silicon steel
Black: Primary winding
Red: Secondary winding
The electrical conductor used for the windings depends upon the application, but in all cases the individual turns must be electrically insulated from each other to ensure that the current travels throughout every turn. For small transformers, in which currents are low and the potential difference between adjacent turns is small, the coils are often wound from enamelled magnet wire. Larger power transformers may be wound with copper rectangular strip conductors insulated by oil-impregnated paper and blocks of pressboard.
High-frequency transformers operating in the tens to hundreds of kilohertz often have windings made of braided Litz wire to minimize the skin-effect and proximity effect losses. Large power transformers use multiple-stranded conductors as well, since even at low power frequencies non-uniform distribution of current would otherwise exist in high-current windings. Each strand is individually insulated, and the strands are arranged so that at certain points in the winding, or throughout the whole winding, each portion occupies different relative positions in the complete conductor. The transposition equalizes the current flowing in each strand of the conductor, and reduces eddy current losses in the winding itself. The stranded conductor is also more flexible than a solid conductor of similar size, aiding manufacture.
The windings of signal transformers minimize leakage inductance and stray capacitance to improve high-frequency response. Coils are split into sections, and those sections interleaved between the sections of the other winding.
Power-frequency transformers may have taps at intermediate points on the winding, usually on the higher voltage winding side, for voltage adjustment. Taps may be manually reconnected, or a manual or automatic switch may be provided for changing taps. Automatic on-load tap changers are used in electric power transmission or distribution, on equipment such as arc furnace transformers, or for automatic voltage regulators for sensitive loads. Audio-frequency transformers, used for the distribution of audio to public address loudspeakers, have taps to allow adjustment of impedance to each speaker. A center-tapped transformer is often used in the output stage of an audio power amplifier in a push-pull circuit. Modulation transformers in AM transmitters are very similar.
Cooling

It is a rule of thumb that the life expectancy of electrical insulation is halved for about every 7 °C to 10 °C increase in operating temperature (an instance of the application of the Arrhenius equation).
Small dry-type and liquid-immersed transformers are often self-cooled by natural convection and radiation heat dissipation. As power ratings increase, transformers are often cooled by forced-air cooling, forced-oil cooling, water-cooling, or combinations of these. Large transformers are filled with transformer oil that both cools and insulates the windings. Transformer oil is often a highly refined mineral oil that cools the windings and insulation by circulating within the transformer tank. The mineral oil and paper insulation system has been extensively studied and used for more than 100 years. It is estimated that 50% of power transformers will survive 50 years of use, that the average age of failure of power transformers is about 10 to 15 years, and that about 30% of power transformer failures are due to insulation and overloading failures. Prolonged operation at elevated temperature degrades insulating properties of winding insulation and dielectric coolant, which not only shortens transformer life but can ultimately lead to catastrophic transformer failure. With a great body of empirical study as a guide, transformer oil testing including dissolved gas analysis provides valuable maintenance information.
Building regulations in many jurisdictions require indoor liquid-filled transformers to either use dielectric fluids that are less flammable than oil, or be installed in fire-resistant rooms. Air-cooled dry transformers can be more economical where they eliminate the cost of a fire-resistant transformer room.
The tank of liquid-filled transformers often has radiators through which the liquid coolant circulates by natural convection or fins. Some large transformers employ electric fans for forced-air cooling, pumps for forced-liquid cooling, or have heat exchangers for water-cooling. An oil-immersed transformer may be equipped with a Buchholz relay, which, depending on severity of gas accumulation due to internal arcing, is used to either trigger an alarm or de-energize the transformer. Oil-immersed transformer installations usually include fire protection measures such as walls, oil containment, and fire-suppression sprinkler systems.
Polychlorinated biphenyls (PCBs) have properties that once favored their use as a dielectric coolant, though concerns over their environmental persistence led to a widespread ban on their use. Today, non-toxic, stable silicone-based oils, or fluorinated hydrocarbons may be used where the expense of a fire-resistant liquid offsets additional building cost for a transformer vault. However, the long life span of transformers can mean that the potential for exposure can be high long after banning.
Some transformers are gas-insulated. Their windings are enclosed in sealed, pressurized tanks and often cooled by nitrogen or sulfur hexafluoride gas.
Experimental power transformers in the 500–1,000 kVA range have been built with liquid nitrogen or helium cooled superconducting windings, which eliminates winding losses without affecting core losses.
Insulation

Insulation must be provided between the individual turns of the windings, between the windings, between windings and core, and at the terminals of the winding.
Inter-turn insulation of small transformers may be a layer of insulating varnish on the wire. Layer of paper or polymer films may be inserted between layers of windings, and between primary and secondary windings. A transformer may be coated or dipped in a polymer resin to improve the strength of windings and protect them from moisture or corrosion. The resin may be impregnated into the winding insulation using combinations of vacuum and pressure during the coating process, eliminating all air voids in the winding. In the limit, the entire coil may be placed in a mold, and resin cast around it as a solid block, encapsulating the windings.
Large oil-filled power transformers use windings wrapped with insulating paper, which is impregnated with oil during assembly of the transformer. Oil-filled transformers use highly refined mineral oil to insulate and cool the windings and core. Construction of oil-filled transformers requires that the insulation covering the windings be thoroughly dried of residual moisture before the oil is introduced. Drying may be done by circulating hot air around the core, by circulating externally heated transformer oil, or by vapor-phase drying (VPD) where an evaporated solvent transfers heat by condensation on the coil and core. For small transformers, resistance heating by injection of current into the windings is used.
Bushings
Larger transformers are provided with high-voltage insulated bushings made of polymers or porcelain. A large bushing can be a complex structure since it must provide careful control of the electric field gradient without letting the transformer leak oil.
Classification parameters


Transformers can be classified in many ways, such as the following:
- Power rating: From a fraction of a volt-ampere (VA) to over a thousand MVA.
- Duty of a transformer: Continuous, short-time, intermittent, periodic, varying.
- Frequency range: Power-frequency, audio-frequency, or radio-frequency.
- Voltage class: From a few volts to hundreds of kilovolts.
- Cooling type: Dry or liquid-immersed; self-cooled, forced air-cooled;forced oil-cooled, water-cooled.
- Application: power supply, impedance matching, output voltage and current stabilizer, pulse, circuit isolation, power distribution, rectifier, arc furnace, amplifier output, etc..
- Basic magnetic form: Core form, shell form, concentric, sandwich.
- Constant-potential transformer descriptor: Step-up, step-down, isolation.
- General winding configuration: By IEC vector group, two-winding combinations of the phase designations delta, wye or star, and zigzag; autotransformer, Scott-T
- Rectifier phase-shift winding configuration: 2-winding, 6-pulse; 3-winding, 12-pulse; . . ., n-winding, ·6-pulse; polygon; etc..
Applications

Various specific electrical application designs require a variety of transformer types. Although they all share the basic characteristic transformer principles, they are customized in construction or electrical properties for certain installation requirements or circuit conditions.
In electric power transmission, transformers allow transmission of electric power at high voltages, which reduces the loss due to heating of the wires. This allows generating plants to be located economically at a distance from electrical consumers. All but a tiny fraction of the world's electrical power has passed through a series of transformers by the time it reaches the consumer.
In many electronic devices, a transformer is used to convert voltage from the distribution wiring to convenient values for the circuit requirements, either directly at the power line frequency or through a switch mode power supply.
Signal and audio transformers are used to couple stages of amplifiers and to match devices such as microphones and record players to the input of amplifiers. Audio transformers allowed telephone circuits to carry on a two-way conversation over a single pair of wires. A balun transformer converts a signal that is referenced to ground to a signal that has balanced voltages to ground, such as between external cables and internal circuits. Isolation transformers prevent leakage of current into the secondary circuit and are used in medical equipment and at construction sites. Resonant transformers are used for coupling between stages of radio receivers, or in high-voltage Tesla coils.

History
Discovery of induction

Electromagnetic induction, the principle of the operation of the transformer, was discovered independently by Michael Faraday in 1831 and Joseph Henry in 1832. Only Faraday furthered his experiments to the point of working out the equation describing the relationship between EMF and magnetic flux now known as Faraday's law of induction:
where is the magnitude of the EMF in volts and ΦB is the magnetic flux through the circuit in webers.
Faraday performed early experiments on induction between coils of wire, including winding a pair of coils around an iron ring, thus creating the first toroidal closed-core transformer. However he only applied individual pulses of current to his transformer, and never discovered the relation between the turns ratio and EMF in the windings.

Induction coils
Main article: Induction coil
The first type of transformer to see wide use was the induction coil, invented by Irish-Catholic Rev. Nicholas Callan of Maynooth College, Ireland in 1836. He was one of the first researchers to realize the more turns the secondary winding has in relation to the primary winding, the larger the induced secondary EMF will be. Induction coils evolved from scientists' and inventors' efforts to get higher voltages from batteries. Since batteries produce direct current (DC) rather than AC, induction coils relied upon vibrating electrical contacts that regularly interrupted the current in the primary to create the flux changes necessary for induction. Between the 1830s and the 1870s, efforts to build better induction coils, mostly by trial and error, slowly revealed the basic principles of transformers.
First alternating current transformers
By the 1870s, efficient generators producing alternating current (AC) were available, and it was found AC could power an induction coil directly, without an interrupter.
In 1876, Russian engineer Pavel Yablochkov invented a lighting system based on a set of induction coils where the primary windings were connected to a source of AC. The secondary windings could be connected to several 'electric candles' (arc lamps) of his own design. The coils Yablochkov employed functioned essentially as transformers.
In 1878, the Ganz factory, Budapest, Hungary, began producing equipment for electric lighting and, by 1883, had installed over fifty systems in Austria-Hungary. Their AC systems used arc and incandescent lamps, generators, and other equipment.
In 1882, Lucien Gaulard and John Dixon Gibbs first exhibited a device with an initially widely criticized laminated plate open iron core called a 'secondary generator' in London, then sold the idea to the Westinghouse company in the United States in 1886. They also exhibited the invention in Turin, Italy in 1884, where it was highly successful and adopted for an electric lighting system. Their open-core device used a fixed 1:1 ratio to supply a series circuit for the utilization load (lamps). The voltage was controlled by moving the iron core in or out.
Early series circuit transformer distribution
Induction coils with open magnetic circuits are inefficient at transferring power to loads. Until about 1880, the paradigm for AC power transmission from a high voltage supply to a low voltage load was a series circuit. Open-core transformers with a ratio near 1:1 were connected with their primaries in series to allow use of a high voltage for transmission while presenting a low voltage to the lamps. The inherent flaw in this method was that turning off a single lamp (or other electric device) affected the voltage supplied to all others on the same circuit. Many adjustable transformer designs were introduced to compensate for this problematic characteristic of the series circuit, including those employing methods of adjusting the core or bypassing the magnetic flux around part of a coil. Efficient, practical transformer designs did not appear until the 1880s, but within a decade, the transformer would be instrumental in the war of the currents, and in seeing AC distribution systems triumph over their DC counterparts, a position in which they have remained dominant ever since.



Closed-core transformers and parallel power distribution
In the autumn of 1884, Károly Zipernowsky, Ottó Bláthy and Miksa Déri (ZBD), three Hungarian engineers associated with the Ganz Works, had determined that open-core devices were impracticable, as they were incapable of reliably regulating voltage. The Ganz factory had also in the autumn of 1884 made delivery of the world's first five high-efficiency AC transformers, the first of these units having been shipped on September 16, 1884. This first unit had been manufactured to the following specifications: 1,400 W, 40 Hz, 120:72 V, 11.6:19.4 A, ratio 1.67:1, one-phase, shell form. In their joint 1885 patent applications for novel transformers (later called ZBD transformers), they described two designs with closed magnetic circuits where copper windings were either wound around an iron wire ring core or surrounded by an iron wire core. The two designs were the first application of the two basic transformer constructions in common use to this day, termed "core form" or "shell form" .
In both designs, the magnetic flux linking the primary and secondary windings traveled almost entirely within the confines of the iron core, with no intentional path through air (see Toroidal cores below). The new transformers were 3.4 times more efficient than the open-core bipolar devices of Gaulard and Gibbs. The ZBD patents included two other major interrelated innovations: one concerning the use of parallel connected, instead of series connected, utilization loads, the other concerning the ability to have high turns ratio transformers such that the supply network voltage could be much higher (initially 1,400 to 2,000 V) than the voltage of utilization loads (100 V initially preferred). When employed in parallel connected electric distribution systems, closed-core transformers finally made it technically and economically feasible to provide electric power for lighting in homes, businesses and public spaces. Bláthy had suggested the use of closed cores, Zipernowsky had suggested the use of parallel shunt connections, and Déri had performed the experiments; In early 1885, the three engineers also eliminated the problem of eddy current losses with the invention of the lamination of electromagnetic cores.
Transformers today are designed on the principles discovered by the three engineers. They also popularized the word 'transformer' to describe a device for altering the EMF of an electric current although the term had already been in use by 1882. In 1886, the ZBD engineers designed, and the Ganz factory supplied electrical equipment for, the world's first power station that used AC generators to power a parallel connected common electrical network, the steam-powered Rome-Cerchi power plant.
Westinghouse improvements

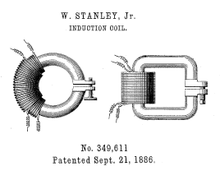
Building on the advancement of AC technology in Europe, George Westinghouse founded the Westinghouse Electric in Pittsburgh, Pennsylvania, on January 8, 1886. The new firm became active in developing alternating current (AC) electric infrastructure throughout the United States. The Edison Electric Light Company held an option on the US rights for the ZBD transformers, requiring Westinghouse to pursue alternative designs on the same principles. George Westinghouse had bought Gaulard and Gibbs' patents for $50,000 in February 1886. He assigned to William Stanley the task of redesign the Gaulard and Gibbs transformer for commercial use in United States. Stanley's first patented design was for induction coils with single cores of soft iron and adjustable gaps to regulate the EMF present in the secondary winding (see image). This design was first used commercially in the US in 1886 but Westinghouse was intent on improving the Stanley design to make it (unlike the ZBD type) easy and cheap to produce.
Westinghouse, Stanley and associates soon developed a core that was easier to manufacture, consisting of a stack of thin 'E‑shaped' iron plates insulated by thin sheets of paper or other insulating material. Pre-wound copper coils could then be slid into place, and straight iron plates laid in to create a closed magnetic circuit. Westinghouse obtained a patent for the new low-cost design in 1887.
Other early transformer designs
In 1889, Russian-born engineer Mikhail Dolivo-Dobrovolsky developed the first three-phase transformer at the Allgemeine Elektricitäts-Gesellschaft ('General Electricity Company') in Germany.
In 1891, Nikola Tesla invented the Tesla coil, an air-cored, dual-tuned resonant transformer for producing very high voltages at high frequency.
Audio frequency transformers ("repeating coils") were used by early experimenters in the development of the telephone.
See also
- High-voltage transformer fire barriers
- Inductive coupling
- Load profile
- Magnetization
- Parametric transformer
- Polyphase system
- Power inverter
- Rectiformer
- Voltage converter
Notes
- With turns of the winding oriented perpendicularly to the magnetic field lines, the flux is the product of the magnetic flux density and the core area, the magnetic field varying with time according to the excitation of the primary. The expression , defined as the derivative of magnetic flux with time , provides a measure of rate of magnetic flux in the core and hence of EMF induced in the respective winding. The negative sign in eq. 1 & eq. 2 is consistent with Lenz's law and Faraday's law in that by convention EMF "induced by an increase of magnetic flux linkages is opposite to the direction that would be given by the right-hand rule."
- Although ideal transformer's winding inductances are each infinitely high, the square root of winding inductances' ratio is equal to the turns ratio.
- This also implies the following: The net core flux is zero, the input impedance is infinite when secondary is open and zero when secondary is shorted; there is zero phase-shift through an ideal transformer; input and output power and reactive volt-ampere are each conserved; these three statements apply for any frequency above zero and periodic waveforms are conserved.
- Direction of transformer currents is according to the Right-Hand Rule.
- Percent impedance is the ratio of the voltage drop in the secondary from no load to full load.
References
- Bedell, Frederick (1942). "History of A-C Wave Form, Its Determination and Standardization". Transactions of the American Institute of Electrical Engineers. 61 (12): 864. doi:10.1109/T-AIEE.1942.5058456. S2CID 51658522.
- Skilling, Hugh Hildreth (1962). Electromechanics. John Wiley & Sons, Inc. p. 39
- ^ Brenner & Javid 1959, §18-6 The Ideal Transformer, pp. 598–600
- Brenner & Javid 1959, §18-1 Symbols and Polarity of Mutual Inductance, pp.=589–590
- Crosby 1958, p. 145
- Paul A. Tipler, Physics, Worth Publishers, Inc., 1976 ISBN 0-87901-041-X, pp. 937-940
- Flanagan, William M. (1993). Handbook of Transformer Design & Applications (2nd ed.). McGraw-Hill. ISBN 978-0-07-021291-6. pp. 2-1, 2-2
- Electrical Engineering: An Introduction. Saunders College Publishing. 1984. p. 610. ISBN 0-03-061758-8.
- ^ Say, M. G. (1983). Alternating Current Machines (5th ed.). London: Pitman. ISBN 978-0-273-01969-5.
- L. Dalessandro, F. d. S. Cavalcante, and J. W. Kolar, "Self-Capacitance of High-Voltage Transformers," IEEE Transactions on Power Electronics, vol. 22, no. 5, pp. 2081–2092, 2007.
- ^ McLaren 1984, pp. 68–74
- ^ Calvert, James (2001). "Inside Transformers". University of Denver. Archived from the original on May 9, 2007. Retrieved May 19, 2007.
- Terman, Frederick E. (1955). Electronic and Radio Engineering (4th ed.). New York: McGraw-Hill. pp. 15.
- Heathcote 1998, p. 4
- Knowlton, A.E., ed. (1949). Standard Handbook for Electrical Engineers (8th ed.). McGraw-Hill. p. see esp. Section 6 Transformers, etc, pp. 547–644. Nomenclature for Parallel Operation, pp. 585–586
- ^ Daniels 1985, pp. 47–49
- "400 Hz Electrical Systems". Aerospaceweb.org. Retrieved May 21, 2007.
- ^ De Keulenaer et al. 2001
- Kubo, T.; Sachs, H.; Nadel, S. (2001). Opportunities for New Appliance and Equipment Efficiency Standards. American Council for an Energy-Efficient Economy. p. 39, fig. 1. Retrieved June 21, 2009.
- ^ Heathcote 1998, pp. 41–42
- "Understanding Transformer Noise" (PDF). FP. Archived from the original (PDF) on 10 May 2006. Retrieved 30 January 2013.
- ^ Nailen, Richard (May 2005). "Why We Must Be Concerned With Transformers". Electrical Apparatus. Archived from the original on 2009-04-29.
- Pansini 1999, p. 23
- ^ Del Vecchio et al. 2002, pp. 10–11, Fig. 1.8
- Hydroelectric Research and Technical Services Group. "Transformers: Basics, Maintenance, and Diagnostics" (PDF). U.S. Dept. of the Interior, Bureau of Reclamation. p. 12. Retrieved Mar 27, 2012.
- ^ US Army Corps of Engineers (1994). "EM 1110-2-3006 Engineering and Design – Hydroelectric Power Plants Electrical Design". Chapter 4 Power Transformers. p. 4-1.
- ^ Hindmarsh 1977, pp. 29–31
- Gottlieb 1998, p. 4
- ^ Allan, D.J. (Jan 1991). "Power Transformers – The Second Century". Power Engineering Journal. 5 (1): 5–14. doi:10.1049/pe:19910004 (inactive 7 December 2024).
{{cite journal}}: CS1 maint: DOI inactive as of December 2024 (link) - Kulkarni & Khaparde 2004, pp. 36–37
- ^ McLyman 2004, pp. 3-9 to 3-14
- ^ Harlow 2004, §2.1.7 & §2.1.6.2.1 in Section §2.1 Power Transformers by H. Jin Sim and Scott H. Digby in Chapter 2 Equipment Types
- Boteler, D. H.; Pirjola, R. J.; Nevanlinna, H. (1998). "The Effects of Geomagnetic Disturbances On Electrical Systems at the Earth's Surface". Advances in Space Research. 22 (1): 17–27. Bibcode:1998AdSpR..22...17B. doi:10.1016/S0273-1177(97)01096-X.
- Hasegawa, Ryusuke (June 2, 2000). "Present Status of Amorphous Soft Magnetic Alloys". Journal of Magnetism and Magnetic Materials. 215–216 (1): 240–245. Bibcode:2000JMMM..215..240H. doi:10.1016/S0304-8853(00)00126-8.
- McLyman 2004, p. 3-1
- "Toroidal Line Power Transformers. Power Ratings Tripled. | Magnetics Magazine". www.magneticsmagazine.com. Archived from the original on 2016-09-24. Retrieved 2016-09-23.
- Lee, Reuben. "Air-Core Transformers". Electronic Transformers and Circuits. Retrieved May 22, 2007.
- ^ CEGB 1982
- Dixon, Lloyd (2001). "Power Transformer Design" (PDF). Magnetics Design Handbook. Texas Instruments.
- ^ Harlow 2004, §3.4.8 in Section 3.4 Load and Thermal Performance by Robert F. Tillman in Chapter 3 Ancillary Topics
- Pansini 1999, p. 32
- ^ H. Lee Willis, Power Distribution Planning Reference Book, 2004 CRC Press. ISBN 978-0-8247-4875-3, pg. 403
- Hartley, William H. (2003). Analysis of Transformer Failures. 36th Annual Conference of the International Association of Engineering Insurers. p. 7 (fig. 6). Archived from the original on 20 October 2013. Retrieved 30 January 2013.
{{cite conference}}: CS1 maint: numeric names: authors list (link) - Hartley, William H. (~2011). "An Analysis of Transformer Failures, Part 1 – 1988 through 1997". The Locomotive. Archived from the original on 18 June 2018. Retrieved 30 January 2013.
{{cite web}}: CS1 maint: numeric names: authors list (link) - "ASTDR ToxFAQs for Polychlorinated Biphenyls". 2001. Retrieved June 10, 2007.
- ^ Kulkarni & Khaparde 2004, pp. 2–3
- "What silicone wristbands say about chemical exposure in Uruguayan children". www.buffalo.edu. Retrieved 2022-01-28.
- Mehta, S.P.; Aversa, N.; Walker, M.S. (Jul 1997). "Transforming Transformers [Superconducting windings]" (PDF). IEEE Spectrum. 34 (7): 43–49. doi:10.1109/6.609815. Retrieved 14 November 2012.
- Pansini 1999, pp. 66–67
- Lane, Keith (2007) (June 2007). "The Basics of Large Dry-Type Transformers". EC&M. Retrieved 29 January 2013.
{{cite web}}: CS1 maint: numeric names: authors list (link) - Ryan 2004, pp. 416–417
- Heathcote 1998, p. 1
- Poyser, Arthur William (1892). Magnetism and Electricity: A Manual for Students in Advanced Classes. London and New York: Longmans, Green, & Co. p. 285, fig. 248.
- "A Brief History of Electromagnetism" (PDF).
- "Electromagnetism". Smithsonian Institution Archives.
- MacPherson, Ph.D., Ryan C. Joseph Henry: The Rise of an American scientist. Archived from the original on 2015-12-08. Retrieved 2015-10-28.
- ^ Guarnieri 2013, pp. 56–59
- Chow, Tai L. (2006). Introduction to Electromagnetic Theory: A Modern Perspective. Sudbury, Mass.: Jones and Bartlett Publishers. p. 171. ISBN 978-0-7637-3827-3.
- Faraday, Michael (1834). "Experimental Researches on Electricity, 7th Series". Philosophical Transactions of the Royal Society. 124: 77–122. doi:10.1098/rstl.1834.0008. S2CID 116224057.
- "Stanley Transformer – 1886 - MagLab". Archived from the original on 2017-10-11. Retrieved 2021-07-27.
- ^ Hughes 1993, pp. 95–96
- ^ Uppenborn, F. J. (1889). History of the Transformer. London: E. & F. N. Spon. pp. 35–41.
- Halacsy, Andrew; Fuchs, George (April 1961). "Transformer Invented 75 Years Ago". Transactions of the American Institute of Electrical Engineers. Part III: Power Apparatus and Systems. 80 (3): 121–125. doi:10.1109/AIEEPAS.1961.4500994. S2CID 51632693. Archived from the original on November 28, 2023. Retrieved November 28, 2023.
{{cite journal}}: CS1 maint: bot: original URL status unknown (link) - Coltman 1988, pp. 86–95
- ^ Halacsy & Von Fuchs 1961, pp. 121–125
- Lucas, J.R. "Historical Development of the Transformer" (PDF). IEE Sri Lanka Centre. Retrieved Mar 1, 2012.
- Jeszenszky, Sándor. "Electrostatics and Electrodynamics at Pest University in the Mid-19th Century" (PDF). University of Pavia. Archived from the original on June 27, 2022. Retrieved Mar 3, 2012.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - "Hungarian Inventors and Their Inventions". Institute for Developing Alternative Energy in Latin America. Archived from the original on 2012-03-22. Retrieved Mar 3, 2012.
- "Bláthy, Ottó Titusz". Budapest University of Technology and Economics, National Technical Information Centre and Library. Retrieved Feb 29, 2012.
- ^ Smil, Vaclav (2005). Creating the Twentieth Century: Technical Innovations of 1867–1914 and Their Lasting Impact. Oxford: Oxford University Press. p. 71. ISBN 978-0-19-803774-3.
ZBD transformer.
- Electrical Society of Cornell University (1896). Proceedings of the Electrical Society of Cornell University. Andrus & Church. p. 39.
- Nagy, Árpád Zoltán (Oct 11, 1996). "Lecture to Mark the 100th Anniversary of the Discovery of the Electron in 1897 (preliminary text)". Budapest. Archived from the original on November 25, 2012. Retrieved July 9, 2009.
- Oxford English Dictionary (2nd ed.). Oxford University Press. 1989.
- Hospitalier, Édouard (1882). The Modern Applications of Electricity. Translated by Julius Maier. New York: D. Appleton & Co. p. 103.
- "Ottó Bláthy, Miksa Déri, Károly Zipernowsky". IEC Techline. Archived from the original on 2010-12-06. Retrieved Apr 16, 2010.
- Brusso, Barry; Allerhand, Adam (January 2021). "A Contrarian History of Early Electric Power Distribution". IEEE Industry Applications Magazine. IEEE.org: 12. doi:10.1109/MIAS.2020.3028630. S2CID 230605234. Archived from the original on December 12, 2020. Retrieved January 1, 2023.
- History of Tinicum Township (PA) 1643–1993 (PDF). Tinicum Township Historical Society. 1993. Archived (PDF) from the original on April 23, 2015.
- William R. Huber (2022). George Westinghouse Powering the World. McFarland & Company. p. 84. ISBN 9781476686929.
- Skrabec, Quentin R. (2007). George Westinghouse: Gentle Genius. Algora Publishing. p. 102. ISBN 978-0-87586-508-9.
- ^ Coltman 2002
- International Electrotechnical Commission. Otto Blathy, Miksa Déri, Károly Zipernowsky. Archived from the original on December 6, 2010. Retrieved May 17, 2007.
{{cite book}}:|work=ignored (help) - Neidhöfer, Gerhard (2008). Michael von Dolivo-Dobrowolsky and Three-Phase: The Beginnings of Modern e Technology and Power Supply (in German). In collaboration with VDE "History of Electrical Engineering" Committee (2nd ed.). Berlin: VDE-Verl. ISBN 978-3-8007-3115-2.
- Uth, Robert (Dec 12, 2000). "Tesla Coil". Tesla: Master of Lightning. PBS.org. Retrieved May 20, 2008.
- "telephone | History, Definition, Invention, Uses, & Facts | Britannica". www.britannica.com. Retrieved 2022-07-17.
Bibliography
- Beeman, Donald, ed. (1955). Industrial Power Systems Handbook. McGraw-Hill.
- Calvert, James (2001). "Inside Transformers". University of Denver. Archived from the original on May 9, 2007. Retrieved May 19, 2007.
- Coltman, J. W. (Jan 1988). "The Transformer". Scientific American. 258 (1): 86–95. Bibcode:1988SciAm.258a..86C. doi:10.1038/scientificamerican0188-86. OSTI 6851152.
- Coltman, J. W. (Jan–Feb 2002). "The Transformer [Historical Overview]". IEEE Industry Applications Magazine. 8 (1): 8–15. doi:10.1109/2943.974352. S2CID 18160717.
- Brenner, Egon; Javid, Mansour (1959). "Chapter 18–Circuits with Magnetic Coupling". Analysis of Electric Circuits. McGraw-Hill. pp. 586–622.
- CEGB, (Central Electricity Generating Board) (1982). Modern Power Station Practice. Pergamon. ISBN 978-0-08-016436-6.
- Crosby, D. (1958). "The Ideal Transformer". IRE Transactions on Circuit Theory. 5 (2): 145. doi:10.1109/TCT.1958.1086447.
- Daniels, A. R. (1985). Introduction to Electrical Machines. Macmillan. ISBN 978-0-333-19627-4.
- De Keulenaer, Hans; Chapman, David; Fassbinder, Stefan; McDermott, Mike (2001). The Scope for Energy Saving in the EU through the Use of Energy-Efficient Electricity Distribution Transformers (PDF). 16th International Conference and Exhibition on Electricity Distribution (CIRED 2001). Institution of Engineering and Technology. doi:10.1049/cp:20010853. Retrieved 10 July 2014.
- Del Vecchio, Robert M.; Poulin, Bertrand; Feghali, Pierre T.M.; Shah, Dilipkumar; Ahuja, Rajendra (2002). Transformer Design Principles: With Applications to Core-Form Power Transformers. Boca Raton: CRC Press. ISBN 978-90-5699-703-8.
- Fink, Donald G.; Beatty, H. Wayne, eds. (1978). Standard Handbook for Electrical Engineers (11th ed.). McGraw Hill. ISBN 978-0-07-020974-9.
- Gottlieb, Irving (1998). Practical Transformer Handbook: for Electronics, Radio and Communications Engineers. Elsevier. ISBN 978-0-7506-3992-7.
- Guarnieri, M. (2013). "Who Invented the Transformer?". IEEE Industrial Electronics Magazine. 7 (4): 56–59. doi:10.1109/MIE.2013.2283834. S2CID 27936000.
- Halacsy, A. A.; Von Fuchs, G. H. (April 1961). "Transformer Invented 75 Years Ago". IEEE Transactions of the American Institute of Electrical Engineers. 80 (3): 121–125. doi:10.1109/AIEEPAS.1961.4500994. S2CID 51632693.
- Hameyer, Kay (2004). Electrical Machines I: Basics, Design, Function, Operation (PDF). RWTH Aachen University Institute of Electrical Machines. Archived from the original (PDF) on 2013-02-10.
- Hammond, John Winthrop (1941). Men and Volts: The Story of General Electric. J. B. Lippincott Company. pp. see esp. 106–107, 178, 238.
- Harlow, James (2004). Electric Power Transformer Engineering (PDF). CRC Press. ISBN 0-8493-1704-5.
- Hughes, Thomas P. (1993). Networks of Power: Electrification in Western Society, 1880-1930. Baltimore: The Johns Hopkins University Press. p. 96. ISBN 978-0-8018-2873-7. Retrieved Sep 9, 2009.
- Heathcote, Martin (1998). J & P Transformer Book (12th ed.). Newnes. ISBN 978-0-7506-1158-9.
- Hindmarsh, John (1977). Electrical Machines and Their Applications (4th ed.). Exeter: Pergamon. ISBN 978-0-08-030573-8.
- Kothari, D.P.; Nagrath, I.J. (2010). Electric Machines (4th ed.). Tata McGraw-Hill. ISBN 978-0-07-069967-0.
- Kulkarni, S. V.; Khaparde, S. A. (2004). Transformer Engineering: Design and Practice. CRC Press. ISBN 978-0-8247-5653-6.
- McLaren, Peter (1984). Elementary Electric Power and Machines. Ellis Horwood. ISBN 978-0-470-20057-5.
- McLyman, Colonel William (2004). "Chapter 3". Transformer and Inductor Design Handbook. CRC. ISBN 0-8247-5393-3.
- Pansini, Anthony (1999). Electrical Transformers and Power Equipment. CRC Press. ISBN 978-0-88173-311-2.
- Parker, M. R; Ula, S.; Webb, W. E. (2005). "§2.5.5 'Transformers' & §10.1.3 'The Ideal Transformer'". In Whitaker, Jerry C. (ed.). The Electronics Handbook (2nd ed.). Taylor & Francis. pp. 172, 1017. ISBN 0-8493-1889-0.
- Ryan, H. M. (2004). High Voltage Engineering and Testing. CRC Press. ISBN 978-0-85296-775-1.
External links
General links:
| Electronic components | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Semiconductor devices |
| ||||||||
| Voltage regulators | |||||||||
| Vacuum tubes |
| ||||||||
| Vacuum tubes (RF) | |||||||||
| Cathode-ray tubes | |||||||||
| Gas-filled tubes | |||||||||
| Adjustable | |||||||||
| Passive | |||||||||
| Reactive | |||||||||


 is the
is the  is the
is the 

 is apparent power and
is apparent power and  is
is 
 is winding self-inductance.
is winding self-inductance.


 is the load impedance of the secondary circuit &
is the load impedance of the secondary circuit &  is the apparent load or driving point impedance of the primary circuit, the superscript
is the apparent load or driving point impedance of the primary circuit, the superscript  denoting referred to the primary.
denoting referred to the primary.

 and,
and,


 is the magnitude of the EMF in volts and ΦB is the magnetic flux through the circuit in
is the magnitude of the EMF in volts and ΦB is the magnetic flux through the circuit in  , defined as the derivative of magnetic flux
, defined as the derivative of magnetic flux  with time
with time  , provides a measure of rate of magnetic flux in the core and hence of EMF induced in the respective winding. The negative sign in eq. 1 & eq. 2 is consistent with Lenz's law and Faraday's law in that by convention EMF "induced by an increase of magnetic flux linkages is opposite to the direction that would be given by the
, provides a measure of rate of magnetic flux in the core and hence of EMF induced in the respective winding. The negative sign in eq. 1 & eq. 2 is consistent with Lenz's law and Faraday's law in that by convention EMF "induced by an increase of magnetic flux linkages is opposite to the direction that would be given by the 
