Misplaced Pages

Augmented triangular prism
Type	Johnson J48 – J49 – J50
Faces	6 triangles 2 squares
Edges	13
Vertices	7
Vertex configuration	${\displaystyle {\begin{aligned}&2\times (3\times 4^{2})\,+\\&1\times (3^{4})\,+\\&4\times (3^{3}\times 4)\end{aligned}}}$
Symmetry group	${\displaystyle C_{2\mathrm {v} }}$
Properties	convex
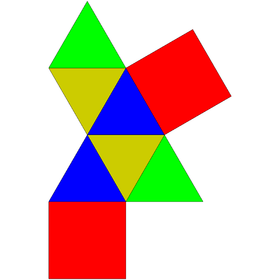
Net

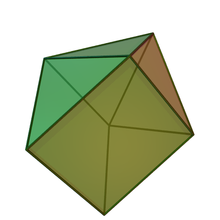
In geometry, the augmented triangular prism is a polyhedron constructed by attaching an equilateral square pyramid onto the square face of a triangular prism. As a result, it is an example of Johnson solid. It can be visualized as the chemical compound, known as capped trigonal prismatic molecular geometry.

Construction

The augmented triangular prism can be constructed from a triangular prism by attaching an equilateral square pyramid to one of its square faces, a process known as augmentation. This square pyramid covers the square face of the prism, so the resulting polyhedron has 6 equilateral triangles and 2 squares as its faces. A convex polyhedron in which all faces are regular is Johnson solid, and the augmented triangular prism is among them, enumerated as 49th Johnson solid ${\displaystyle J_{49}}$.

Properties

An augmented triangular prism with edge length ${\displaystyle a}$ has a surface area, calculated by adding six equilateral triangles and two squares' area: $${\displaystyle {\frac {4+3{\sqrt {3}}}{2}}a^{2}\approx 4.598a^{2}.}$$ Its volume can be obtained by slicing it into a regular triangular prism and an equilateral square pyramid, and adding their volume subsequently: $${\displaystyle {\frac {2{\sqrt {2}}+3{\sqrt {3}}}{12}}a^{3}\approx 0.669a^{3}.}$$

It has three-dimensional symmetry group of the cyclic group ${\displaystyle C_{2\mathrm {v} }}$ of order 4. Its dihedral angle can be calculated by adding the angle of an equilateral square pyramid and a regular triangular prism in the following:

• The dihedral angle of an augmented triangular prism between two adjacent triangles is that of an equilateral square pyramid between two adjacent triangular faces, ${\textstyle \arccos \left(-1/3\right)\approx 109.5^{\circ }}$
• The dihedral angle of an augmented triangular prism between two adjacent squares is that of a triangular prism between two lateral faces, the interior angle of a triangular prism ${\displaystyle \pi /3=60^{\circ }}$.
• The dihedral angle of an augmented triangular prism between square and triangle is the dihedral angle of a triangular prism between the base and its lateral face, ${\textstyle \pi /2=90^{\circ }}$
• The dihedral angle of an equilateral square pyramid between a triangular face and its base is ${\textstyle \arctan \left({\sqrt {2}}\right)\approx 54.7^{\circ }}$. Therefore, the dihedral angle of an augmented triangular prism between a square (the lateral face of the triangular prism) and triangle (the lateral face of the equilateral square pyramid) on the edge where the equilateral square pyramid is attached to the square face of the triangular prism, and between two adjacent triangles (the lateral face of both equilateral square pyramids) on the edge where two equilateral square pyramids are attached adjacently to the triangular prism, are $${\displaystyle {\begin{aligned}\arctan \left({\sqrt {2}}\right)+{\frac {\pi }{3}}&\approx 114.7^{\circ },\\2\arctan \left({\sqrt {2}}\right)+{\frac {\pi }{3}}&\approx 169.4^{\circ }.\end{aligned}}}$$

Application

In the geometry of chemical compounds, a polyhedron may commonly visualize an atom cluster surrounding a central atom. The capped trigonal prismatic molecular geometry describes clusters for which this polyhedron is an augmented triangular prism. An example of such compound is the potassium heptafluorotantalate.

See also

• Biaugmented triangular prism — the 50th Johnson solid, constructed by attaching a triangular prism with two equilateral square pyramids.
• Triaugmented triangular prism — the 51st Johnson solid, constructed by attaching a triangular prism with three equilateral square pyramids.

References

1. Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. p. 84–89. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
2. ^ Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
3. Francis, Darryl (August 2013). "Johnson solids & their acronyms". Word Ways. 46 (3): 177.
4. Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
5. Hoffmann, Roald; Beier, Barbara F.; Muetterties, Earl L.; Rossi, Angelo R. (1977). "Seven-coordination. A molecular orbital exploration of structure, stereochemistry, and reaction dynamics". Inorganic Chemistry. 16 (3): 511–522. doi:10.1021/ic50169a002.
6. Kaupp, Martin (2001). ""Non-VSEPR" Structures and Bonding in d(0) Systems". Angew Chem Int Ed Engl. 40 (1): 3534–3565. doi:10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#. PMID 11592184.

External links

• Weisstein, Eric W. "Johnson Solid". MathWorld.
  • Weisstein, Eric W. "Augmented triangular prism". MathWorld.

• Johnson solids