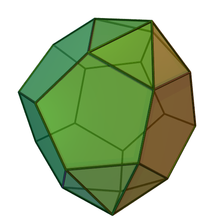
| Metabiaugmented dodecahedron | |
|---|---|
 | |
| Type | Johnson J59 – J60 – J61 |
| Faces | 2+2.4 triangles 3.2+4 pentagons |
| Edges | 40 |
| Vertices | 22 |
| Vertex configuration | 3.2+4(5) 2+2.4(3.5) 2(3) |
| Symmetry group | C2v |
| Dual polyhedron | - |
| Properties | convex |
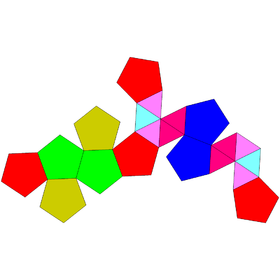
| Net | |
 | |
In geometry, the metabiaugmented dodecahedron is one of the Johnson solids (J60). It can be viewed as a dodecahedron with two pentagonal pyramids (J2) attached to two faces that are separated by one face. (The two faces are not opposite, but not adjacent either.) When pyramids are attached to a dodecahedron in other ways, they may result in an augmented dodecahedron (J58), a parabiaugmented dodecahedron (J59), a triaugmented dodecahedron (J61), or even a pentakis dodecahedron if the faces are made to be irregular.
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
External links
This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it. |
- Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.