Misplaced Pages

In geometry, polyhedra are three-dimensional objects where points are connected by lines to form polygons. The points, lines, and polygons of a polyhedron are referred to as its vertices, edges, and faces, respectively. A polyhedron is considered to be convex if:

• The shortest path between any two of its vertices lies either within its interior or on its boundary.
• None of its faces are coplanar—they do not share the same plane and do not "lie flat".
• None of its edges are colinear—they are not segments of the same line.

A convex polyhedron whose faces are regular polygons is known as a Johnson solid, or sometimes as a Johnson–Zalgaller solid. Some authors exclude uniform polyhedra from the definition. A uniform polyhedron is a polyhedron in which the faces are regular and they are isogonal; examples include Platonic and Archimedean solids as well as prisms and antiprisms. The Johnson solids are named after American mathematician Norman Johnson (1930–2017), who published a list of 92 such polyhedra in 1966. His conjecture that the list was complete and no other examples existed was proven by Russian-Israeli mathematician Victor Zalgaller (1920–2020) in 1969.

Some of the Johnson solids may be categorized as elementary polyhedra, meaning they cannot be separated by a plane to create two small convex polyhedra with regular faces. The Johnson solids satisfying this criteria are the first six—equilateral square pyramid, pentagonal pyramid, triangular cupola, square cupola, pentagonal cupola, and pentagonal rotunda. The criteria is also satisfied by eleven other Johnson solids, specifically the tridiminished icosahedron, parabidiminished rhombicosidodecahedron, tridiminished rhombicosidodecahedron, snub disphenoid, snub square antiprism, sphenocorona, sphenomegacorona, hebesphenomegacorona, disphenocingulum, bilunabirotunda, and triangular hebesphenorotunda. The rest of the Johnson solids are not elementary, and they are constructed using the first six Johnson solids together with Platonic and Archimedean solids in various processes. Augmentation involves attaching the Johnson solids onto one or more faces of polyhedra, while elongation or gyroelongation involve joining them onto the bases of a prism or antiprism, respectively. Some others are constructed by diminishment, the removal of one of the first six solids from one or more of a polyhedron's faces.

The following table contains the 92 Johnson solids, with edge length ${\displaystyle a}$. The table includes the solid's enumeration (denoted as ${\displaystyle J_{n}}$). It also includes the number of vertices, edges, and faces of each solid, as well as its symmetry group, surface area ${\displaystyle A}$, and volume ${\displaystyle V}$. Every polyhedron has its own characteristics, including symmetry and measurement. An object is said to have symmetry if there is a transformation that maps it to itself. All of those transformations may be composed in a group, alongside the group's number of elements, known as the order. In two-dimensional space, these transformations include rotating around the center of a polygon and reflecting an object around the perpendicular bisector of a polygon. A polygon that is rotated symmetrically by ${\textstyle {\frac {360^{\circ }}{n}}}$ is denoted by ${\displaystyle C_{n}}$, a cyclic group of order ${\displaystyle n}$; combining this with the reflection symmetry results in the symmetry of dihedral group ${\displaystyle D_{n}}$ of order ${\displaystyle 2n}$. In three-dimensional symmetry point groups, the transformations preserving a polyhedron's symmetry include the rotation around the line passing through the base center, known as the axis of symmetry, and the reflection relative to perpendicular planes passing through the bisector of a base, which is known as the pyramidal symmetry ${\displaystyle C_{n\mathrm {v} }}$ of order ${\displaystyle 2n}$. The transformation that preserves a polyhedron's symmetry by reflecting it across a horizontal plane is known as the prismatic symmetry ${\displaystyle D_{n\mathrm {h} }}$ of order ${\displaystyle 4n}$. The antiprismatic symmetry ${\displaystyle D_{n\mathrm {d} }}$ of order ${\displaystyle 4n}$ preserves the symmetry by rotating its half bottom and reflection across the horizontal plane. The symmetry group ${\displaystyle C_{n\mathrm {h} }}$ of order ${\displaystyle 2n}$ preserves the symmetry by rotation around the axis of symmetry and reflection on the horizontal plane; the specific case preserving the symmetry by one full rotation is ${\displaystyle C_{1\mathrm {h} }}$ of order 2, often denoted as ${\displaystyle C_{s}}$. The mensuration of polyhedra includes the surface area and volume. An area is a two-dimensional measurement calculated by the product of length and width; for a polyhedron, the surface area is the sum of the areas of all of its faces. A volume is a measurement of a region in three-dimensional space. The volume of a polyhedron may be ascertained in different ways: either through its base and height (like for pyramids and prisms), by slicing it off into pieces and summing their individual volumes, or by finding the root of a polynomial representing the polyhedron.

The 92 Johnson solids

${\displaystyle J_{n}}$	Solid name	Image	Vertices	Edges	Faces	Symmetry group and its order	Surface area and volume
1	Equilateral square pyramid		5	8	5	${\displaystyle C_{4v}}$ of order 8	${\displaystyle {\begin{aligned}A&=\left(1+{\sqrt {3}}\right)a^{2}\\&\approx 2.7321a^{2}\\V&={\frac {\sqrt {2}}{6}}a^{3}\\&\approx 0.2357a^{3}\end{aligned}}}$
2	Pentagonal pyramid		6	10	6	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {a^{2}}{2}}{\sqrt {{\frac {5}{2}}\left(10+{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\\&\approx 3.8855a^{2}\\V&=\left({\frac {5+{\sqrt {5}}}{24}}\right)a^{3}\\&\approx 0.3015a^{3}\end{aligned}}}$
3	Triangular cupola		9	15	8	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&=\left(3+{\frac {5{\sqrt {3}}}{2}}\right)a^{2}\\&\approx 7.3301a^{2}\\V&=\left({\frac {5}{3{\sqrt {2}}}}\right)a^{3}\\&\approx 1.1785a^{3}\end{aligned}}}$
4	Square cupola		12	20	10	${\displaystyle C_{4v}}$ of order 8	${\displaystyle {\begin{aligned}A&=\left(7+2{\sqrt {2}}+{\sqrt {3}}\right)a^{2}\\&\approx 11.5605a^{2}\\V&=\left(1+{\frac {2{\sqrt {2}}}{3}}\right)a^{3}\\&\approx 1.9428a^{3}\end{aligned}}}$
5	Pentagonal cupola		15	25	12	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&=\left({\frac {1}{4}}\left(20+5{\sqrt {3}}+{\sqrt {5\left(145+62{\sqrt {5}}\right)}}\right)\right)a^{2}\\&\approx 16.5798a^{2}\\V&=\left({\frac {1}{6}}\left(5+4{\sqrt {5}}\right)\right)a^{3}\\&\approx 2.3241a^{3}\end{aligned}}}$
6	Pentagonal rotunda		20	35	17	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&=\left({\frac {1}{2}}\left(5{\sqrt {3}}+{\sqrt {10\left(65+29{\sqrt {5}}\right)}}\right)\right)a^{2}\\&\approx 22.3472a^{2}\\V&=\left({\frac {1}{12}}\left(45+17{\sqrt {5}}\right)\right)a^{3}\\&\approx 6.9178a^{3}\end{aligned}}}$
7	Elongated triangular pyramid		7	12	7	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&=\left(3+{\sqrt {3}}\right)a^{2}\\&\approx 4.7321a^{2}\\V&=\left({\frac {1}{12}}\left({\sqrt {2}}+3{\sqrt {3}}\right)\right)a^{3}\\&\approx 0.5509a^{3}\end{aligned}}}$
8	Elongated square pyramid		9	16	9	${\displaystyle C_{4v}}$ of order 8	${\displaystyle {\begin{aligned}A&=\left(5+{\sqrt {3}}\right)a^{2}\\&\approx 6.7321a^{2}\\V&=\left(1+{\frac {\sqrt {2}}{6}}\right)a^{3}\\&\approx 1.2357a^{3}\end{aligned}}}$
9	Elongated pentagonal pyramid		11	20	11	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {20+5{\sqrt {3}}+{\sqrt {25+10{\sqrt {5}}}}}{4}}a^{2}\\&\approx 8.8855a^{2}\\V&=\left({\frac {5+{\sqrt {5}}+6{\sqrt {25+10{\sqrt {5}}}}}{24}}\right)a^{3}\\&\approx 2.022a^{3}\end{aligned}}}$
10	Gyroelongated square pyramid		9	20	13	${\displaystyle C_{4v}}$ of order 8	${\displaystyle {\begin{aligned}A&=(1+3{\sqrt {3}})a^{2}\\&\approx 6.1962a^{2}\\V&={\frac {1}{6}}\left({\sqrt {2}}+2{\sqrt {4+3{\sqrt {2}}}}\right)a^{3}\\&\approx 1.1927a^{3}\end{aligned}}}$
11	Gyroelongated pentagonal pyramid		11	25	16	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(15{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 8.2157a^{2}\\V&={\frac {1}{24}}\left(25+9{\sqrt {5}}\right)a^{3}\\&\approx 1.8802a^{3}\end{aligned}}}$
12	Triangular bipyramid		5	9	6	${\displaystyle D_{3h}}$ of order 12	${\displaystyle {\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}a^{2}\\&\approx 2.5981a^{2}\\V&={\frac {\sqrt {2}}{6}}a^{3}\\&\approx 0.2358a^{3}\end{aligned}}}$
13	Pentagonal bipyramid		7	15	10	${\displaystyle D_{5h}}$ of order 20	${\displaystyle {\begin{aligned}A&={\frac {5{\sqrt {3}}}{2}}a^{2}\\&\approx 4.3301a^{2}\\V&={\frac {1}{12}}\left(5+{\sqrt {5}}\right)a^{3}\\&\approx 0.603a^{3}\end{aligned}}}$
14	Elongated triangular bipyramid		8	15	9	${\displaystyle D_{3h}}$ of order 12	${\displaystyle {\begin{aligned}A&={\frac {3}{2}}\left(2+{\sqrt {3}}\right)a^{2}\\&\approx 5.5981a^{2}\\V&={\frac {1}{12}}\left(2{\sqrt {2}}+3{\sqrt {3}}\right)a^{3}\\&\approx 0.6687a^{3}\end{aligned}}}$
15	Elongated square bipyramid		10	20	12	${\displaystyle D_{4h}}$ of order 16	${\displaystyle {\begin{aligned}A&=2\left(2+{\sqrt {3}}\right)a^{2}\\&\approx 7.4641a^{2}\\V&={\frac {1}{3}}\left(3+{\sqrt {2}}\right)a^{3}\\&\approx 1.4714a^{3}\end{aligned}}}$
16	Elongated pentagonal bipyramid		12	25	15	${\displaystyle D_{5h}}$ of order 20	${\displaystyle {\begin{aligned}A&={\frac {5}{2}}\left(2+{\sqrt {3}}\right)a^{2}\\&\approx 9.3301a^{2}\\V&={\frac {1}{12}}\left(5+{\sqrt {5}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{3}\\&\approx 2.3235a^{3}\end{aligned}}}$
17	Gyroelongated square bipyramid		10	24	16	${\displaystyle D_{4d}}$ of order 16	${\displaystyle {\begin{aligned}A&=4{\sqrt {3}}a^{2}\\&\approx 6.9282a^{2}\\V&={\frac {1}{3}}\left({\sqrt {2}}+{\sqrt {4+3{\sqrt {2}}}}\right)a^{3}\\&\approx 1.4284a^{3}\end{aligned}}}$
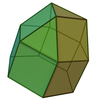
18	Elongated triangular cupola		15	27	14	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}\left(18+5{\sqrt {3}}\right)a^{2}\\&\approx 13.3301a^{2}\\V&={\frac {1}{6}}\left(5{\sqrt {2}}+9{\sqrt {3}}\right)a^{3}\\&\approx 3.7766a^{3}\end{aligned}}}$
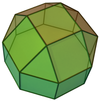
19	Elongated square cupola		20	36	18	${\displaystyle C_{4v}}$ of order 8	${\displaystyle {\begin{aligned}A&=(15+2{\sqrt {2}}+{\sqrt {3}})a^{2}\\&\approx 19.5605a^{2}\\V&=\left(3+{\frac {8{\sqrt {2}}}{3}}\right)a^{3}\\&\approx 6.7712a^{3}\end{aligned}}}$
20	Elongated pentagonal cupola		25	45	22	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(60+5{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 26.5798a^{2}\\V&={\frac {1}{6}}\left(5+4{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)a^{3}\\&\approx 10.0183a^{3}\end{aligned}}}$
21	Elongated pentagonal rotunda		30	55	27	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}a^{2}\left(20+5{\sqrt {3}}+5{\sqrt {5+2{\sqrt {5}}}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)\\&\approx 32.3472a^{2}\\V&={\frac {1}{12}}a^{3}\left(45+17{\sqrt {5}}+30{\sqrt {5+2{\sqrt {5}}}}\right)\\&\approx 14.612a^{3}\end{aligned}}}$
22	Gyroelongated triangular cupola		15	33	20	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}\left(6+11{\sqrt {3}}\right)a^{2}\\&\approx 12.5263a^{2}\\V&={\frac {1}{3}}{\sqrt {{\frac {61}{2}}+18{\sqrt {3}}+30{\sqrt {1+{\sqrt {3}}}}}}a^{3}\\&\approx 3.5161a^{3}\end{aligned}}}$
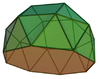
23	Gyroelongated square cupola		20	44	26	${\displaystyle C_{4v}}$ of order 8	${\displaystyle {\begin{aligned}A&=(7+2{\sqrt {2}}+5{\sqrt {3}})a^{2}\\&\approx 18.4887a^{2}\\V&=\left(1+{\frac {2}{3}}{\sqrt {2}}+{\frac {2}{3}}{\sqrt {4+2{\sqrt {2}}+2{\sqrt {146+103{\sqrt {2}}}}}}\right)a^{3}\\&\approx 6.2108a^{3}\end{aligned}}}$
24	Gyroelongated pentagonal cupola		25	55	32	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(20+25{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 25.2400a^{2}\\V&=\left({\frac {5}{6}}+{\frac {2}{3}}{\sqrt {5}}+{\frac {5}{6}}{\sqrt {2{\sqrt {650+290{\sqrt {5}}}}-2{\sqrt {5}}-2}}\right)a^{3}\\&\approx 9.0733a^{3}\end{aligned}}}$
25	Gyroelongated pentagonal rotunda		30	65	37	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}\left(15{\sqrt {3}}+\left(5+3{\sqrt {5}}\right){\sqrt {5+2{\sqrt {5}}}}\right)a^{2}\\&\approx 31.0075a^{2}\\V&=\left({\frac {45}{12}}+{\frac {17}{12}}{\sqrt {5}}+{\frac {5}{6}}{\sqrt {2{\sqrt {650+290{\sqrt {5}}}}-2{\sqrt {5}}-2}}\right)a^{3}\\&\approx 13.6671a^{3}\end{aligned}}}$
26	Gyrobifastigium		8	14	8	${\displaystyle D_{2d}}$ of order 8	${\displaystyle {\begin{aligned}A&=\left(4+{\sqrt {3}}\right)a^{2}\\&\approx 5.7321a^{2}\\V&=\left({\frac {\sqrt {3}}{2}}\right)a^{3}\\&\approx 0.866a^{3}\end{aligned}}}$
27	Triangular orthobicupola		12	24	14	${\displaystyle D_{3h}}$ of order 12	${\displaystyle {\begin{aligned}A&=2\left(3+{\sqrt {3}}\right)a^{2}\\&\approx 9.4641a^{2}\\V&={\frac {5{\sqrt {2}}}{3}}a^{3}\\&\approx 2.357a^{3}\end{aligned}}}$
28	Square orthobicupola		16	32	18	${\displaystyle D_{4h}}$ of order 16	${\displaystyle {\begin{aligned}A&=2(5+{\sqrt {3}})a^{2}\\&\approx 13.4641a^{2}\\V&=\left(2+{\frac {4{\sqrt {2}}}{3}}\right)a^{3}\\&\approx 3.8856a^{3}\end{aligned}}}$
29	Square gyrobicupola		16	32	18	${\displaystyle D_{4d}}$ of order 16	${\displaystyle {\begin{aligned}A&=2(5+{\sqrt {3}})a^{2}\\&\approx 13.4641a^{2}\\V&=\left(2+{\frac {4{\sqrt {2}}}{3}}\right)a^{3}\\&\approx 3.8856a^{3}\end{aligned}}}$
30	Pentagonal orthobicupola		20	40	22	${\displaystyle D_{5h}}$ of order 20	${\displaystyle {\begin{aligned}A&=\left(10+{\sqrt {{\frac {5}{2}}\left(10+{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\right)a^{2}\\&\approx 17.7711a^{2}\\V&={\frac {1}{3}}\left(5+4{\sqrt {5}}\right)a^{3}\\&\approx 4.6481a^{3}\end{aligned}}}$
31	Pentagonal gyrobicupola		20	40	22	${\displaystyle D_{5d}}$ of order 20	${\displaystyle {\begin{aligned}A&=\left(10+{\sqrt {{\frac {5}{2}}\left(10+{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\right)a^{2}\\&\approx 17.7711a^{2}\\V&={\frac {1}{3}}\left(5+4{\sqrt {5}}\right)a^{3}\\&\approx 4.6481a^{3}\end{aligned}}}$
32	Pentagonal orthocupolarotunda		25	50	27	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&=\left(5+{\frac {1}{4}}{\sqrt {1900+490{\sqrt {5}}+210{\sqrt {75+30{\sqrt {5}}}}}}\right)a^{2}\\&\approx 23.5385a^{2}\\V&={\frac {5}{12}}\left(11+5{\sqrt {5}}\right)a^{3}\\&\approx 9.2418a^{3}\end{aligned}}}$
33	Pentagonal gyrocupolarotunda		25	50	27	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&=\left(5+{\frac {15}{4}}{\sqrt {3}}+{\frac {7}{4}}{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\\&\approx 23.5385a^{2}\\V&={\frac {5}{12}}\left(11+5{\sqrt {5}}\right)a^{3}\\&\approx 9.2418a^{3}\end{aligned}}}$
34	Pentagonal orthobirotunda		30	60	32	${\displaystyle D_{5h}}$ of order 20	${\displaystyle {\begin{aligned}A&=\left((5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 29.306a^{2}\\V&={\frac {1}{6}}(45+17{\sqrt {5}})a^{3}\\&\approx 13.8355a^{3}\end{aligned}}}$
35	Elongated triangular orthobicupola		18	36	20	${\displaystyle D_{3h}}$ of order 12	${\displaystyle {\begin{aligned}A&=2(6+{\sqrt {3}})a^{2}\\&\approx 15.4641a^{2}\\V&=\left({\frac {5{\sqrt {2}}}{3}}+{\frac {3{\sqrt {3}}}{2}}\right)a^{3}\\&\approx 4.9551a^{3}\end{aligned}}}$
36	Elongated triangular gyrobicupola		18	36	20	${\displaystyle D_{3d}}$ of order 12	${\displaystyle {\begin{aligned}A&=2(6+{\sqrt {3}})a^{2}\\&\approx 15.4641a^{2}\\V&=\left({\frac {5{\sqrt {2}}}{3}}+{\frac {3{\sqrt {3}}}{2}}\right)a^{3}\\&\approx 4.9551a^{3}\end{aligned}}}$
37	Elongated square gyrobicupola		24	48	26	${\displaystyle D_{4d}}$ of order 16	${\displaystyle {\begin{aligned}A&=2(9+{\sqrt {3}})a^{2}\\&\approx 21.4641a^{2}\\V&=\left(4+{\frac {10{\sqrt {2}}}{3}}\right)a^{3}\\&\approx 8.714a^{3}\end{aligned}}}$
38	Elongated pentagonal orthobicupola		30	60	32	${\displaystyle D_{5h}}$ of order 20	${\displaystyle {\begin{aligned}A&=\left(20+{\sqrt {{\frac {5}{2}}\left(10+{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\right)a^{2}\\&\approx 27.7711a^{2}\\V&={\frac {1}{6}}\left(10+8{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)a^{3}\\&\approx 12.3423a^{3}\end{aligned}}}$
39	Elongated pentagonal gyrobicupola		30	60	32	${\displaystyle D_{5d}}$ of order 20	${\displaystyle {\begin{aligned}A&=\left(20+{\sqrt {{\frac {5}{2}}\left(10+{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\right)a^{2}\\&\approx 27.7711a^{2}\\V&={\frac {1}{6}}\left(10+8{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)a^{3}\\&\approx 12.3423a^{3}\end{aligned}}}$
40	Elongated pentagonal orthocupolarotunda		35	70	37	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(60+{\sqrt {10\left(190+49{\sqrt {5}}+21{\sqrt {75+30{\sqrt {5}}}}\right)}}\right)a^{2}\\&\approx 33.5385a^{2}\\V&={\frac {5}{12}}\left(11+5{\sqrt {5}}+6{\sqrt {5+2{\sqrt {5}}}}\right)a^{3}\\&\approx 16.936a^{3}\end{aligned}}}$
41	Elongated pentagonal gyrocupolarotunda		35	70	37	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(60+{\sqrt {10\left(190+49{\sqrt {5}}+21{\sqrt {75+30{\sqrt {5}}}}\right)}}\right)a^{2}\\&\approx 33.5385a^{2}\\V&={\frac {5}{12}}\left(11+5{\sqrt {5}}+6{\sqrt {5+2{\sqrt {5}}}}\right)a^{3}\\&\approx 16.936a^{3}\end{aligned}}}$
42	Elongated pentagonal orthobirotunda		40	80	42	${\displaystyle D_{5h}}$ of order 20	${\displaystyle {\begin{aligned}A&=\left(10+{\sqrt {30\left(10+3{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\right)a^{2}\\&\approx 39.306a^{2}\\V&={\frac {1}{6}}\left(45+17{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)a^{3}\\&\approx 21.5297a^{3}\end{aligned}}}$
43	Elongated pentagonal gyrobirotunda		40	80	42	${\displaystyle D_{5d}}$ of order 20	${\displaystyle {\begin{aligned}A&=\left(10+{\sqrt {30\left(10+3{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\right)a^{2}\\&\approx 39.306a^{2}\\V&={\frac {1}{6}}\left(45+17{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)a^{3}\\&\approx 21.5297a^{3}\end{aligned}}}$
44	Gyroelongated triangular bicupola		18	42	26	${\displaystyle D_{3}}$ of order 6	${\displaystyle {\begin{aligned}A&=\left(6+5{\sqrt {3}}\right)a^{2}\\&\approx 14.6603a^{2}\\V&={\sqrt {2}}\left({\frac {5}{3}}+{\sqrt {1+{\sqrt {3}}}}\right)a^{3}\\&\approx 4.6946a^{3}\end{aligned}}}$
45	Gyroelongated square bicupola		24	56	34	${\displaystyle D_{4}}$ of order 8	${\displaystyle {\begin{aligned}A&=\left(10+6{\sqrt {3}}\right)a^{2}\\&\approx 20.3923a^{2}\\V&=\left(2+{\frac {4}{3}}{\sqrt {2}}+{\frac {2}{3}}{\sqrt {4+2{\sqrt {2}}+2{\sqrt {146+103{\sqrt {2}}}}}}\right)a^{3}\\&\approx 8.1536a^{3}\end{aligned}}}$
46	Gyroelongated pentagonal bicupola		30	70	42	${\displaystyle D_{5}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}\left(20+15{\sqrt {3}}+{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\\&\approx 26.4313a^{2}\\V&=\left({\frac {5}{3}}+{\frac {4}{3}}{\sqrt {5}}+{\frac {5}{6}}{\sqrt {2{\sqrt {650+290{\sqrt {5}}}}-2{\sqrt {5}}-2}}\right)a^{3}\\&\approx 11.3974a^{3}\end{aligned}}}$
47	Gyroelongated pentagonal cupolarotunda		35	80	47	${\displaystyle C_{5}}$ of order 5	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(20+35{\sqrt {3}}+7{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\\&\approx 32.1988a^{2}\\V&=\left({\frac {55}{12}}+{\frac {25}{12}}{\sqrt {5}}+{\frac {5}{6}}{\sqrt {2{\sqrt {650+290{\sqrt {5}}}}-2{\sqrt {5}}-2}}\right)a^{3}\\&\approx 15.9911a^{3}\end{aligned}}}$
48	Gyroelongated pentagonal birotunda		40	90	52	${\displaystyle D_{5}}$ of order 10	${\displaystyle {\begin{aligned}A&=\left(10{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\\&\approx 37.9662a^{2}\\V&=\left({\frac {45}{6}}+{\frac {17}{6}}{\sqrt {5}}+{\frac {5}{6}}{\sqrt {2{\sqrt {650+290{\sqrt {5}}}}-2{\sqrt {5}}-2}}\right)a^{3}\\&\approx 20.5848a^{3}\end{aligned}}}$
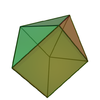
49	Augmented triangular prism		7	13	8	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}(4+3{\sqrt {3}})a^{2}\\&\approx 4.5981a^{2}\\V&={\frac {1}{12}}(2{\sqrt {2}}+3{\sqrt {3}})a^{3}\\&\approx 0.6687a^{3}\end{aligned}}}$
50	Biaugmented triangular prism		8	17	11	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}(2+5{\sqrt {3}})a^{2}\\&\approx 5.3301a^{2}\\V&={\sqrt {{\frac {59}{144}}+{\frac {1}{\sqrt {6}}}}}a^{3}\\&\approx 0.9044a^{3}\end{aligned}}}$
51	Triaugmented triangular prism		9	21	14	${\displaystyle D_{3h}}$ of order 12	${\displaystyle {\begin{aligned}A&={\frac {7{\sqrt {3}}}{2}}a^{2}\\&\approx 6.0622a^{2}\\V&={\frac {2{\sqrt {2}}+{\sqrt {3}}}{4}}a^{3}\\&\approx 1.1401a^{3}\end{aligned}}}$
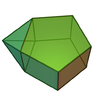
52	Augmented pentagonal prism		11	19	10	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}\left(8+2{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 9.173a^{2}\\V&={\frac {1}{12}}{\sqrt {233+90{\sqrt {5}}+12{\sqrt {50+20{\sqrt {5}}}}}}a^{3}\\&\approx 1.9562a^{3}\end{aligned}}}$
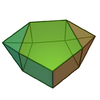
53	Biaugmented pentagonal prism		12	23	13	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}a^{2}\left(6+4{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)\\&\approx 9.9051a^{2}\\V&={\frac {1}{12}}a^{3}{\sqrt {257+90{\sqrt {5}}+24{\sqrt {50+20{\sqrt {5}}}}}}\\&\approx 2.1919a^{3}\end{aligned}}}$
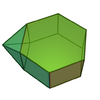
54	Augmented hexagonal prism		13	22	11	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&=(5+4{\sqrt {3}})a^{2}\\&\approx 11.9282a^{2}\\V&={\frac {1}{6}}\left({\sqrt {2}}+9{\sqrt {3}}\right)a^{3}\\&\approx 2.8338a^{3}\end{aligned}}}$
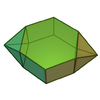
55	Parabiaugmented hexagonal prism		14	26	14	${\displaystyle D_{2h}}$ of order 8	${\displaystyle {\begin{aligned}A&=(4+5{\sqrt {3}})a^{2}\\&\approx 12.6603a^{2}\\V&={\frac {1}{6}}\left(2{\sqrt {2}}+9{\sqrt {3}}\right)a^{3}\\&\approx 3.0695a^{3}\end{aligned}}}$
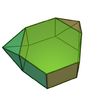
56	Metabiaugmented hexagonal prism		14	26	14	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&=(4+5{\sqrt {3}})a^{2}\\&\approx 12.6603a^{2}\\V&={\frac {1}{6}}\left(2{\sqrt {2}}+9{\sqrt {3}}\right)a^{3}\\&\approx 3.0695a^{3}\end{aligned}}}$
57	Triaugmented hexagonal prism		15	30	17	${\displaystyle D_{3h}}$ of order 12	${\displaystyle {\begin{aligned}A&=3\left(1+2{\sqrt {3}}\right)a^{2}\\&\approx 13.3923a^{2}\\V&=\left({\frac {1}{\sqrt {2}}}+{\frac {3{\sqrt {3}}}{2}}\right)a^{3}\\&\approx 3.3052a^{3}\end{aligned}}}$
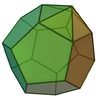
58	Augmented dodecahedron		21	35	16	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(5{\sqrt {3}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 21.0903a^{2}\\V&={\frac {1}{24}}\left(95+43{\sqrt {5}}\right)a^{3}\\&\approx 7.9646a^{3}\end{aligned}}}$
59	Parabiaugmented dodecahedron		22	40	20	${\displaystyle D_{5d}}$ of order 20	${\displaystyle {\begin{aligned}A&={\frac {5}{2}}\left({\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 21.5349a^{2}\\V&={\frac {1}{6}}\left(25+11{\sqrt {5}}\right)a^{3}\\&\approx 8.2661a^{3}\end{aligned}}}$
60	Metabiaugmented dodecahedron		22	40	20	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&={\frac {5}{2}}\left({\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 21.5349a^{2}\\V&={\frac {1}{6}}\left(25+11{\sqrt {5}}\right)a^{3}\\&\approx 8.2661a^{3}\end{aligned}}}$
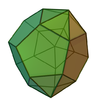
61	Triaugmented dodecahedron		23	45	24	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&={\frac {3}{4}}\left(5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 21.9795a^{2}\\V&={\frac {5}{8}}\left(7+3{\sqrt {5}}\right)a^{3}\\&\approx 8.5676a^{3}\end{aligned}}}$
62	Metabidiminished icosahedron		10	20	12	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}\left(5{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 7.7711a^{2}\\V&={\frac {1}{6}}\left(5+2{\sqrt {5}}\right)a^{3}\\&\approx 1.5787a^{3}\end{aligned}}}$
63	Tridiminished icosahedron		9	15	8	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 7.3265a^{2}\\V&=\left({\frac {5}{8}}+{\frac {7{\sqrt {5}}}{24}}\right)a^{3}\\&\approx 1.2772a^{3}\end{aligned}}}$
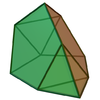
64	Augmented tridiminished icosahedron		10	18	10	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(7{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 8.1925a^{2}\\V&={\frac {1}{24}}\left(15+2{\sqrt {2}}+7{\sqrt {5}}\right)a^{3}\\&\approx 1.395a^{3}\end{aligned}}}$
65	Augmented truncated tetrahedron		15	27	14	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}\left(6+13{\sqrt {3}}\right)a^{2}\\&\approx 14.2583a^{2}\\V&={\frac {11}{2{\sqrt {2}}}}a^{3}\\&\approx 3.8891a^{3}\end{aligned}}}$
66	Augmented truncated cube		28	48	22	${\displaystyle C_{4v}}$ of order 8	${\displaystyle {\begin{aligned}A&=(15+10{\sqrt {2}}+3{\sqrt {3}})a^{2}\\&\approx 34.3383a^{2}\\V&=\left(8+{\frac {16{\sqrt {2}}}{3}}\right)a^{3}\\&\approx 15.5425a^{3}\end{aligned}}}$
67	Biaugmented truncated cube		32	60	30	${\displaystyle D_{4h}}$ of order 16	${\displaystyle {\begin{aligned}A&=2\left(9+4{\sqrt {2}}+2{\sqrt {3}}\right)a^{2}\\&\approx 36.2419a^{2}\\V&=(9+6{\sqrt {2}})a^{3}\\&\approx 17.4853a^{3}\end{aligned}}}$
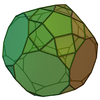
68	Augmented truncated dodecahedron		65	105	42	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(20+25{\sqrt {3}}+110{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 102.1821a^{2}\\V&=\left({\frac {505}{12}}+{\frac {81{\sqrt {5}}}{4}}\right)a^{3}\\&\approx 87.3637a^{3}\end{aligned}}}$
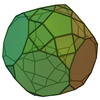
69	Parabiaugmented truncated dodecahedron		70	120	52	${\displaystyle D_{5d}}$ of order 20	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}\left(20+15{\sqrt {3}}+50{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 103.3734a^{2}\\V&={\frac {1}{12}}\left(515+251{\sqrt {5}}\right)a^{3}\\&\approx 89.6878a^{3}\end{aligned}}}$
70	Metabiaugmented truncated dodecahedron		70	120	52	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&={\frac {1}{2}}\left(20+15{\sqrt {3}}+50{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 103.3734a^{2}\\V&={\frac {1}{12}}\left(515+251{\sqrt {5}}\right)a^{3}\\&\approx 89.6878a^{3}\end{aligned}}}$
71	Triaugmented truncated dodecahedron		75	135	62	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(60+35{\sqrt {3}}+90{\sqrt {5+2{\sqrt {5}}}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 104.5648a^{2}\\V&={\frac {7}{12}}\left(75+37{\sqrt {5}}\right)a^{3}\\&\approx 92.0118a^{3}\end{aligned}}}$
72	Gyrate rhombicosidodecahedron		60	120	62	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&=\left(30+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 59.306a^{2}\\V&=\left(20+{\frac {29{\sqrt {5}}}{3}}\right)a^{3}\\&\approx 41.6153a^{3}\end{aligned}}}$
73	Parabigyrate rhombicosidodecahedron		60	120	62	${\displaystyle D_{5d}}$ of order 20	${\displaystyle {\begin{aligned}A&=\left(30+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 59.306a^{2}\\V&=\left(20+{\frac {29{\sqrt {5}}}{3}}\right)a^{3}\\&\approx 41.6153a^{3}\end{aligned}}}$
74	Metabigyrate rhombicosidodecahedron		60	120	62	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&=\left(30+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 59.306a^{2}\\V&=\left(20+{\frac {29{\sqrt {5}}}{3}}\right)a^{3}\\&\approx 41.6153a^{3}\end{aligned}}}$
75	Trigyrate rhombicosidodecahedron		60	120	62	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&=\left(30+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 59.306a^{2}\\V&=\left(20+{\frac {29{\sqrt {5}}}{3}}\right)a^{3}\\&\approx 41.6153a^{3}\end{aligned}}}$
76	Diminished rhombicosidodecahedron		55	105	52	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(100+15{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 58.1147a^{2}\\V&=\left({\frac {115}{6}}+9{\sqrt {5}}\right)a^{3}\\&\approx 39.2913a^{3}\end{aligned}}}$
77	Paragyrate diminished rhombicosidodecahedron		55	105	52	${\displaystyle C_{5v}}$ of order 10	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(100+15{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 58.1147a^{2}\\V&=\left({\frac {115}{6}}+9{\sqrt {5}}\right)a^{3}\\&\approx 39.2913a^{3}\end{aligned}}}$
78	Metagyrate diminished rhombicosidodecahedron		55	105	52	${\displaystyle C_{s}}$ of order 2	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(100+15{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 58.1147a^{2}\\V&=\left({\frac {115}{6}}+9{\sqrt {5}}\right)a^{3}\\&\approx 39.2913a^{3}\end{aligned}}}$
79	Bigyrate diminished rhombicosidodecahedron		55	105	52	${\displaystyle C_{s}}$ of order 2	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(100+15{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 58.1147a^{2}\\V&=\left({\frac {115}{6}}+9{\sqrt {5}}\right)a^{3}\\&\approx 39.2913a^{3}\end{aligned}}}$
80	Parabidiminished rhombicosidodecahedron		50	90	42	${\displaystyle D_{5d}}$ of order 20	${\displaystyle {\begin{aligned}A&={\frac {5}{2}}\left(8+{\sqrt {3}}+2{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 56.9233a^{2}\\V&={\frac {5}{3}}\left(11+5{\sqrt {5}}\right)a^{3}\\&\approx 36.9672a^{3}\end{aligned}}}$
81	Metabidiminished rhombicosidodecahedron		50	90	42	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&={\frac {5}{2}}\left(8+{\sqrt {3}}+2{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 56.9233a^{2}\\V&={\frac {5}{3}}\left(11+5{\sqrt {5}}\right)a^{3}\\&\approx 36.9672a^{3}\end{aligned}}}$
82	Gyrate bidiminished rhombicosidodecahedron		50	90	42	${\displaystyle C_{s}}$ of order 2	${\displaystyle {\begin{aligned}A&={\frac {5}{2}}\left(8+{\sqrt {3}}+2{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 56.9233a^{2}\\V&={\frac {5}{3}}\left(11+5{\sqrt {5}}\right)a^{3}\\&\approx 36.9672a^{3}\end{aligned}}}$
83	Tridiminished rhombicosidodecahedron		45	75	32	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(60+5{\sqrt {3}}+30{\sqrt {5+2{\sqrt {5}}}}+9{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 55.732a^{2}\\V&=\left({\frac {35}{2}}+{\frac {23{\sqrt {5}}}{3}}\right)a^{3}\\&\approx 34.6432a^{3}\end{aligned}}}$
84	Snub disphenoid		8	18	12	${\displaystyle D_{2d}}$ of order 8	${\displaystyle {\begin{aligned}A&=3{\sqrt {3}}a^{2}\\&\approx 5.1962a^{2}\\V&\approx 0.8595a^{3}\end{aligned}}}$
85	Snub square antiprism		16	40	26	${\displaystyle D_{4d}}$ of order 16	${\displaystyle {\begin{aligned}A&=2\left(1+3{\sqrt {3}}\right)a^{2}\\&\approx 12.3923a^{2}\\V&\approx 3.6012a^{3}\end{aligned}}}$
86	Sphenocorona		10	22	14	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&=(2+3{\sqrt {3}})a^{2}\\&\approx 7.1962a^{2}\\V&={\frac {1}{2}}a^{3}{\sqrt {1+3{\sqrt {\frac {3}{2}}}+{\sqrt {13+3{\sqrt {6}}}}}}\\&\approx 1.5154a^{3}\end{aligned}}}$
87	Augmented sphenocorona		11	26	17	${\displaystyle C_{s}}$ of order 2	${\displaystyle {\begin{aligned}A&=(1+4{\sqrt {3}})a^{2}\\&\approx 7.9282a^{2}\\V&={\frac {1}{2}}a^{3}{\sqrt {1+3{\sqrt {\frac {3}{2}}}+{\sqrt {13+3{\sqrt {6}}}}}}+{\frac {1}{3{\sqrt {2}}}}\\&\approx 1.7511a^{3}\end{aligned}}}$
88	Sphenomegacorona		12	28	18	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&=2\left(1+2{\sqrt {3}}\right)a^{2}\\&\approx 8.9282a^{2}\\V&\approx 1.9481a^{3}\end{aligned}}}$
89	Hebesphenomegacorona		14	33	21	${\displaystyle C_{2v}}$ of order 4	${\displaystyle {\begin{aligned}A&={\frac {3}{2}}\left(2+3{\sqrt {3}}\right)a^{2}\\&\approx 10.7942a^{2}\\V&\approx 2.9129a^{3}\end{aligned}}}$
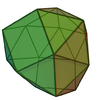
90	Disphenocingulum		16	38	24	${\displaystyle D_{2d}}$ of order 8	${\displaystyle {\begin{aligned}A&=(4+5{\sqrt {3}})a^{2}\\&\approx 12.6603a^{2}\\V&\approx 3.7776a^{3}\end{aligned}}}$
91	Bilunabirotunda		14	26	14	${\displaystyle D_{2h}}$ of order 8	${\displaystyle {\begin{aligned}A&=\left(2+2{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 12.346a^{2}\\V&={\frac {1}{12}}\left(17+9{\sqrt {5}}\right)a^{3}\\&\approx 3.0937a^{3}\end{aligned}}}$
92	Triangular hebesphenorotunda		18	36	20	${\displaystyle C_{3v}}$ of order 6	${\displaystyle {\begin{aligned}A&={\frac {1}{4}}\left(12+19{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)a^{2}\\&\approx 16.3887a^{2}\\V&=\left({\frac {5}{2}}+{\frac {7{\sqrt {5}}}{6}}\right)a^{3}\\&\approx 5.1087a^{3}\end{aligned}}}$